[Algorithm] Insertion sort, Merge sort

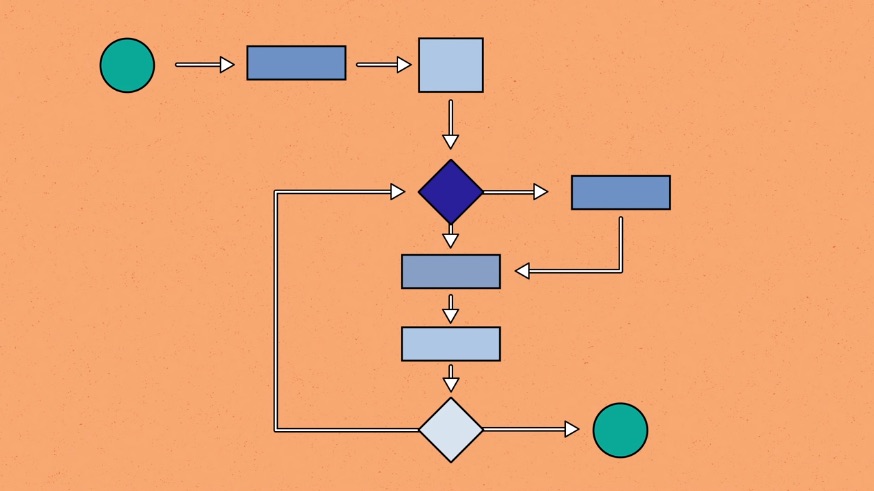
Insertion sort

Insertion sort(삽입정렬)

//pseudo-code
insertion_sort(A, n)
	for i = 2 to n
    	key = A[i]
        j = i - 1
        while j > 0 and A[j] > key
        	A[j + 1] = A[j]
            j = j + 1
        A[j + 1] = key

핵심 개념

• 배열의 요소를 이미 정렬된 sub-array와 비교하며 위치를 찾은 후, 그 위치에 삽입하며 진행된다.
• best case의 경우에는 시간복잡도가 O(n)이지만, average case 시간복잡도는 O(n^2)이다.

Insertion sort in C

//insertion sort program in C
#include <stdio.h>
#define MAX_SIZE 500

void insertion_sort(int *A, int n)
{
  int i, j, key;
  for (i = 1; i < n; i++)
  {
    key = A[i];
    j = i - 1;
    while (j >= 0 && A[j] > key)
    {
      A[j + 1] = A[j];
      j--;
    }
    A[j + 1] = key;
  }
}

int main()
{
  int n;
  int A[MAX_SIZE];

  scanf("%d", &n);
  for (int i = 0; i < n; i++)
  {
    scanf("%d", &A[i]);
  }

  insertion_sort(A, n);

  for (int i = 0; i < n; i++)
  {
    printf("%d ", A[i]);
  }
}

---

Merge sort

Merge sort(병합정렬)

//pseudo-code
merge_sort(A, start, end)
	if p >= r
    	return
    mid = (start + end) / 2
    merge_sort(A, start, mid)
    merge_sort(A, mid + 1, end)
    merge(A, start, mid, end)

핵심 개념

• 분할 정복(문제를 부분 문제로 분할한 후 각각 해결한 다음 다시 합쳐서 전체 문제의 답을 구하는 방식)기법을 사용한다.
• 일반적으로 재귀호출을 이용하여 구현한다.
• 가운데를 기준으로 반을 분할한다. 시간복잡도는 O(n*log_2(n))이다.

Merge sort in C

//merge sort program in C
#include <stdio.h>
#define MAX_SIZE 500

void merge(int *A, int start, int mid, int end)
{
  int length_left = mid - start + 1;
  int length_right = end - mid;

  int i, j, k;
  int L[length_left], R[length_right];

  for (i = 0; i < length_left; i++)
  {
    L[i] = A[start + i];
  }
  for (j = 0; j < length_right; j++)
  {
    R[j] = A[mid + j + 1];
  }

  i = 0;
  j = 0;
  k = start;

  while (i < length_left && j < length_right)
  {
    if (L[i] <= R[j])
    {
      A[k] = L[i];
      i++;
    }
    else
    {
      A[k] = R[j];
      j++;
    }
    k++;
  }

  while (i < length_left)
  {
    A[k] = L[i];
    i++;
    k++;
  }

  while (j < length_right)
  {
    A[k] = R[j];
    j++;
    k++;
  }
}

void merge_sort(int *A, int start, int end)
{
  if (start >= end)
    return;

  int mid = (start + end) / 2;
  merge_sort(A, start, mid);
  merge_sort(A, mid + 1, end);
  merge(A, start, mid, end);
}

int main()
{
  int n;
  int A[MAX_SIZE];

  scanf("%d", &n);
  for (int i = 0; i < n; i++)
  {
    scanf("%d", &A[i]);
  }

  merge_sort(A, 0, n - 1);

  for (int i = 0; i < n; i++)
  {
    printf("%d ", A[i]);
  }
}