[자료구조] Union-Find

📖 서로소 집합(Disjoint-Set)

서로 중복되지 않는 부분 집합들로 나눠진 원소들에 대한 정보를 저장하고 조작하는 자료구조로, 전체 집합이 있을 때 구성 원소들이 겹치지 않도록 분할(partition)하는데 쓰임

• 각 개체들의 집합을 셋(set)이라 한다.
• 셋 A의 모든 원소가 셋 B에 포함될 때 A를 B의 부분집합(subset)이라 한다. 그리고 B를 A의 초월집합(superset)이라 한다.
• 셋 A와 셋 B에 공통된 원소가 하나도 없을 때, 이를 mutually disjoint라 한다.
• 분할(partition)은 다음 두 가지 조건을 만족할 때, 서로소 집합(Disjoint-Set)이 되도록 셋을 쪼개는 것이다.
  (1) 분할된 부분집합을 합치면 원래의 셋이 됨
  (2) 파티션된 부분집합끼리는 mutually disjoint임

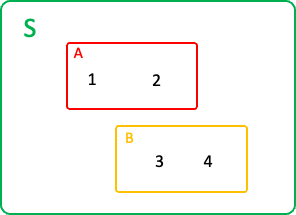
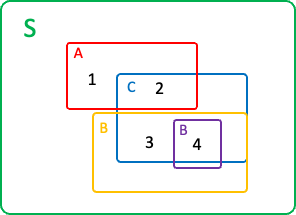
예를 들어, 위 그림 같이 S = [1, 2, 3, 4], A = [1, 2], B = [3, 4], C = [2, 3, 4], D = [4] 일 때 A와 B는 서로소 집합이고 A와 B는 S의 분할이다.

🤷‍ 그래서 Union-Find란?

서로소 집합(Disjoint-Set)을 표현하는 자료구조로, 여러 개의 노드가 연결되어 있는 그래프에서 두 개의 노드를 선택하여 그 노드가 같은 그래프에 속하는지 판별하는 알고리즘이다.

Union(합치기) 연산

• 두 노드가 주어졌을 때, 이 두 노드를 한 그래프로 합친다.

Find(찾기) 연산

• 어떤 노드가 주어졌을 때, 이 노드가 속한 그래프를 반환한다.

📝 어떻게 구현할까?

먼저 index는 node의 번호이고 저장되어 있는 값은 parent node의 번호를 가르키는 그래프가 있다고 해보자.
초기 상태는 각 node들은 parent node가 없이 본인들의 node를 가르키는 서로소 집합으로 아래와 같다.

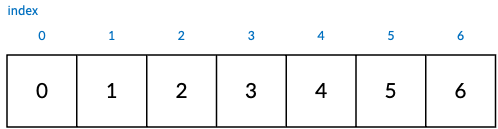
여기서 node 1과 node 3을 union(합치기) 해보자. index에 값이 작은 node를 parent node가 된다.


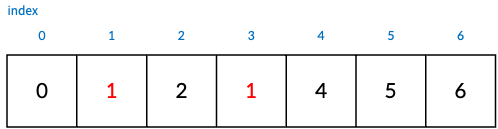
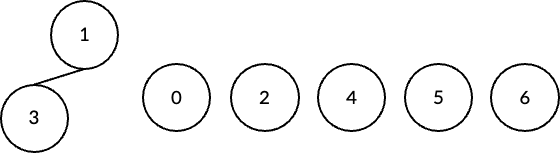
위와 같이 node 3이 node 1을 가리키도록 한다.
한번 더 해보자. node 2가 node 3을 가르키도록 해보자.

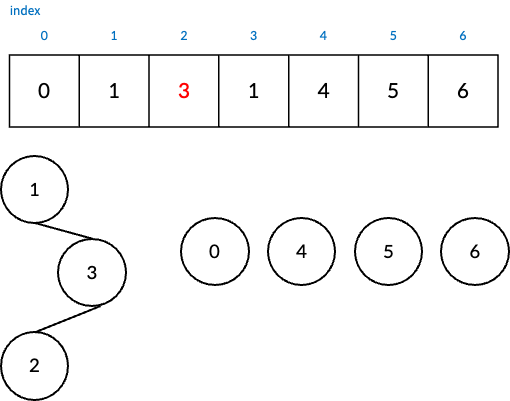
node 2는 parent node로 node 3을 가르키고 있지만, node 3은 node 1을 가르키고 있다.
이럴 때, 더 이상 parent node가 없을 때(본인을 가르킬 때) 까지 최상위 parent node를 찾아주는 과정인 find(찾기) 연산을 해주어야 한다.
재귀적인 방법으로 상위 node가 가르키는 parent node를 찾아주는 것이다.
그렇게 해서 node 2가 가르키는 node 3의 parent node인 1을 가르키게 된다.

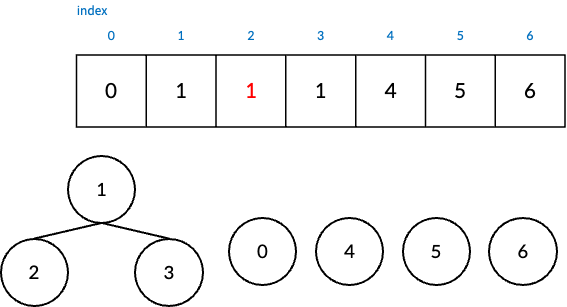
def find(node) :
    if graph[node] != node :
        graph[node] = find(graph[node])
    return graph[node]

def union(node1, node2) :
    node1_parent = find(node1)
    node2_parent = find(node2)
    if node1_parent < node2_parent:
        graph[node2_parent] = node1_parent
    else:
        graph[node1_parent] = node2_parent