index

• query마다 table의 모든 row를 탐색하는 것은 비효율적
• DB의 query 속도를 향상시키기 위해 사용

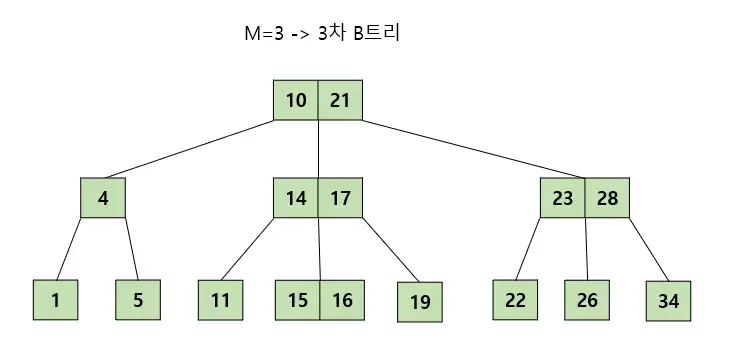
B-tree

• binary tree의 확장이며, 자식 node의 개수가 2개 이상 가능

1. 항상 sorting되어 있음
2. node는 M/2 ~ M 개의 자식을 가질 수 있음 (M차 b-tree)
3. node는 M/2-1 ~ M-1개의 data(key)를 가질 수 있음
4. node의 data가 k개 일 때, 자식은 k+1개
5. node의 왼쪽 자식들은 그 node보다 작고, 오른쪽 자식들은 큼
6. leaf node의 level이 모두 같아야 함 (balanced tree)
   - 따라서, avg/worst case의 조회 시간이 일정함 O(log n)
   

time complexity

• b tree와 다른 tree간 time complexity는 동일함
• 그런데 DB index로 b tree를 사용하는 이유?
  • 보조기억장치에서 data를 읽을 때, block 단위로 읽어들임
  • M차 B tree에서 한 node에서 M개의 자식 node를 가질 수 있음
    • 더 적은 edge로 root -> leaf까지 이동 가능
  • M차 B tree에서 한 node에서 M-1개의 key값을 가질 수 있음
    • block을 효율적으로 활용 가능
• hash index도 존재하지만, 범위 검색 및 정렬 불가능

탐색

• root node에서 출발
• key 값을 따라 내려가면 됨

삽입

• root node부터 조회 후 위치 확인
• leaf node에 삽입
• 2, 3, 4 특성 위반 시 meidan을 부모 node에 삽입

삭제

• 삭제도 항상 leaf node에서 발생
  • internal node를 삭제하려면 leaf node와 위치를 바꾼 후 삭제한다

• 영상을 보는 것을 추천

B+tree

• leaf node에 값(data node)이 저장되며, 그 외의 node에는 key값(index node)만 저장됨
• 모든 leaf node는 linked list

ref
https://code-lab1.tistory.com/217
https://ssocoit.tistory.com/217
https://youtu.be/bqkcoSm_rCs