BackTracking
"가능한 모든 방법을 탐색한다"의 아이디어를 가진다.
즉, 백트래킹은 현재 상태에서 가능한 모든 후보군을 따라 들어가며 해결책에 대한 후보를 구축해 나아가다 가능성이 없다가 판단되면 즉시 후보를 포기하면서 정답을 찾아가는 범용적인 알고리즘이다.
대표적인 완전 탐색 예로 DFS(Depth First Search, 깊이 우선 탐색)이 있다. DFS 는 현재 지점에서 방문할 곳이 있으면 재귀 호출을 이용해서 계속 이동한다
모든 지점을 방문하기 때문에 목표지점이 있지 않은 경로까지 빠져서 비효율적인 결과를 초래하기도 한다.
DFS의 비효율적인 경로를 차단하고 목표지점에 갈 수 있는 가능성이 있는 루트를 검사하는 방법이 백트래킹이다
백트래킹은 DFS에 가지치기 (Pruning) 를 통해 가도되지 않는 루트는 고려하지 않고 탐색하는 완전탐색 기법이다. 가지치기를 얼마나 잘하느냐에 따라서 효율이 극대화 될수 있는 방법이다.
백트래킹은 DFS를 수행하다가, 유망한 노드를 검토하고 만약 유망한 노드라면 그대로 서브트리로 이동하고, 그렇지 않으면 백트래킹을 해 가지치기 하는 방식으로 진행된다.
예제 Combination (조합)
N이 주어졌을 때 1~N까지의 수를 이용하여 k개 만큼의 조합을 구해라.
Input: n = 3, r = 2
Output: [[1, 2], [1, 3], [2, 3]]
풀이
start 부터 n 까지 for 문을 돌린다
1. 탈출 조건 : tempList.size == r || tempList.size > r
2. 깊이 탐색 조건 : if(tempList.contains(nums[i])) continue
: 방문하지 않았을 경우만 backTracking 과정을 실행한다
이때 start : i+1 을 넣어주는데 중복을 허용하지 않기 위함이다.
ex) for(i in 0 until nums.size) 처리 시
OUTPUT : [[1, 2], [1, 3], [2, 1], [2, 3], [3, 1], [3, 2]]
이와 같이 중복이 허용되어 진다.
[1,3] 을 확인한 후 다시 [3] 일때 index 0 부터 for문이 돌아가 [3,1] 을 확인하는 경우가 생긴다.
- 탈출 후 처리 : tempList.removeLast() 탈출 후 마지막에 거친 노드 삭제
- 다시 nums 에서 하나씩 꺼내서 넣는다
class Combination {
lateinit var nums : ArrayList<Int>
fun solve(){
nums = arrayListOf(1,2,3)
val r = 2
val result = ArrayList<ArrayList<Int>>()
backTracking( nums.size, r, 0 ,result, arrayListOf())
println(result)
}
fun backTracking(n : Int, r : Int , start: Int, result: ArrayList<ArrayList<Int>> ,tempList : ArrayList<Int>){
if(tempList.size == r){
result.add(tempList.clone() as ArrayList<Int>)
return
}else if(tempList.size > r) return
for (i in start until nums.size){
if(tempList.contains(nums[i]) ) continue
tempList.add(nums[i])
backTracking(n,r, i+1, result,tempList)
tempList.removeLast()
}
}
}예제 Permutation (순열)
Input : nums = [1,2,3]
Output : [[1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1]]
순열의 가지치기 조건은 중복을 허용하지 않고 모든 수를 한번씩 뽑는 것이다.
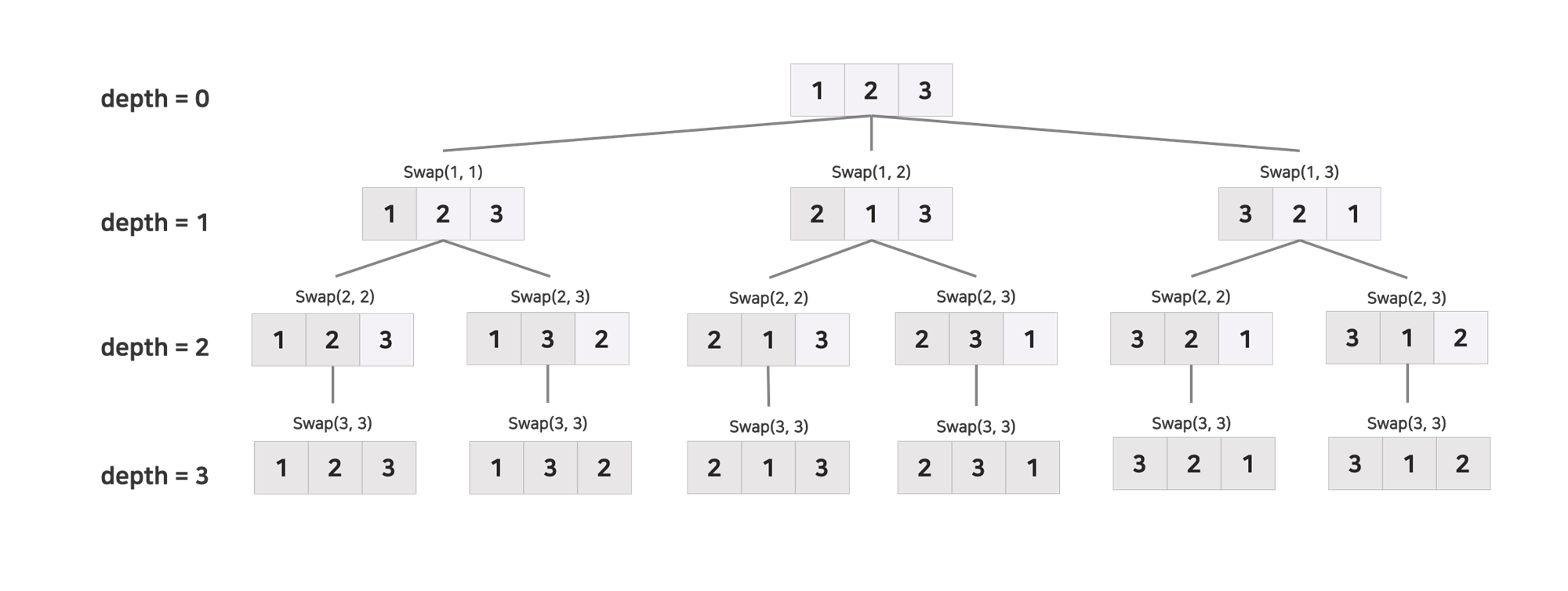
풀이
- 탈출 조건 : tempList.size == nums.size (모두 하나씩 뽑음)
- 깊이 탐색 조건 : if(tempList.contains(nums[i])) continue
: 방문하지 않았을 경우만 backTracking 과정을 실행한다 - 탈출 후 처리 : tempList.removeLast() 탈출 후 마지막에 거친 노드 삭제
- 다시 nums 에서 하나씩 꺼내서 넣는다
class Permutation {
lateinit var nums : ArrayList<Int>
fun solve(){
nums = arrayListOf(1,2,3)
val tempList = arrayListOf<Int>()
val result = ArrayList<MutableList<Int>>()
backTracking(result,tempList)
println(result)
}
fun backTracking(result : ArrayList<MutableList<Int>>, tempList: ArrayList<Int> ) {
if(tempList.isNotEmpty() && tempList.size == nums.size){
val tmp = tempList.clone()
result.add(tmp as ArrayList<Int>)
return
}
for(i in nums.indices){
if(tempList.contains(nums[i])) continue
tempList.add(nums[i])
backTracking(result, tempList)
tempList.removeLast()
}
return
}
}예제 N Queen
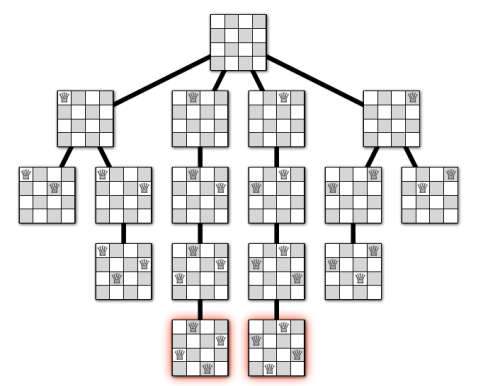
Q. 크기가 N * N 인 체스판 위에 퀸 N 개를 서로 공격할 수 없게 놓는 문제이다.
N이 주어졌을 때, 퀸을 놓는 방법의 수를 구하는 프로그램을 작성하시오.
(퀸은 오와 열, 대각선 이동이 가능한 말이다.)백준 9663 N-Queen
https://www.acmicpc.net/problem/9663
class P9663 {
data class Pos(val row : Int, val col : Int)
var N = 0
var result = 0
var col = Array(15){0}
fun checker(cur : Pos) : Boolean{
//행탐색
for(i in 0 until cur.row){
if((col[i] == col[cur.row] || Math.abs(i-cur.row) == Math.abs(col[i]-cur.col))){
return false
}
}
return true
}
fun backTracking( level : Int){
//대각선과 각 row col에 놓아서는 안 된다
if(level == N ){
result ++
return
}
if(level>=N) return
for(j in 0 until N){
col[level] = j //level번째 행 j열 에 퀸을 놓는다.
if(checker(Pos(level,j))) {
//유망한 노드
backTracking(level+1)
}
}
}
fun solution()=with(System.`in`.bufferedReader()){
N = readLine().toInt()
backTracking(0)
println(result)
}
}처음에는 퀸이 놓여진 지 확인하는 방식은 2차원 Boolean 배열로 관리했다.
이 방식으로 하니 답은 맞지만 시간 초과가 발생했다.
다른 풀이를 참고하니 1차원 배열로 퀸의 위치를 저장하는 방식을 알 수 있었다.
각 행에는 하나의 퀸 밖에 놓을 수 없기 때문에 col[행] = 열 방식으로 저장 할 수 있는 것이다.
checker 에서는 이전에 놓았던 col의 위치 0 ~ 현재 행 까지의 퀸의 위치를 파악해 유망한 노드인지 확인한다.
-
만약 유망한 노드라면 다음 행에 퀸을 놓기 위해 다음 행 level+1 의 탐색을 호출한다
-
유망하지 않다면 같은 행에서 다른 열에 퀸을 놓아보며 유망한 노드를 계속해서 탐색한다

