벨만 포드 알고리즘(Bellman-Ford Algorithm)
다익스트라 알고리즘처럼 그래프에서 한 정점에서 다른 모든 정점으로 가는 최단 경로를 구할 수 있는 알고리즘이다.
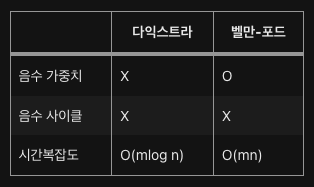
벨만 포드 알고리즘은 다익스트라 알고리즘보다 시간이 더 걸리지만 음의 간선이 존재해도 최단 경로를 찾을 수 있는 알고리즘이다.
벨만포드의 핵심은 음의 간선이 존재해도 최단 경로를 찾을 수 있다는 것이다
벨만 포드 알고리즘도 DP 다이나믹 프로그램의 일종이라 볼 수 있는데
매번 저장해 놓은 최소 비용을 이용해 새로운 최소 비용을 구하는 개념이기 때문이다
Bellman-Ford VS Dijkstra
- 다익스트라 알고리즘: 최소 간선을 우선순위로 하여 경우의 수를 줄여 비용을 절감하는 방식
- 벨만 포드 알고리즘 : 모든 경우의 수를 다 탐색해야 함 (음의 간선이 존재하기 때문)
Flow
정점의 수 : V
- 시작 정점을 선택
- 모든 간선들을 탐색하면서 시작 정점에서 다른 정점까지의 거리가 INF가 아닐 경우에만 거리를 갱신.
- 2번의 과정의
V-1만큼 수행- 음의 사이클을 확인하기 위해 마지막으로 2번을 한번 더 수행
V-1인 이유는 시작 정점 A에서 다른 정점B 까지의 최단 거리는 최대 |V| -1 개의 정점을 지나기 때문이다
V-1 개 이상의 정점을 방문하는 것은 결국 중복 방문을 하는 것이기 때문에 최단 경로가 성립될 수 없다
ex) 1에서 4까지의 최단 경로를 구할 때 최대의 경우의 수는 1-2-3-4 로 3이다. 사이클이 존재한다면 1-2-3-2-3-2-3... 의 경우가 생길 수 있다는 것
4번에서 음의 사이클을 확인하기 위해 2번을 수행하는 이유는
만약 V 개의 정점을 지났는데 최단 경로가 갱신이 된다면 음의 사이클이 발생한 것이며 비용이 무한하게 갱신이 되기 때문에 최단 경로를 구할 수 없기 때문이다.
갱신 조건
d[T] <= d[S] + w(S,T)
T : 해당 간선이 도달하고자 하는 정점
S : 해당 간선의 시작점
d : 시작점에서 해당 정점의 거리
w : 해당 간선의 가중치
알고리즘
각 정점들의 거리를 저장하는 1차원 배열 Dist를 INF 로 초기화 하여 정의한다.
시작 노드를 1 이라고 하면
1. 노드 1에서 다른 정점까지의 거리를 구한다
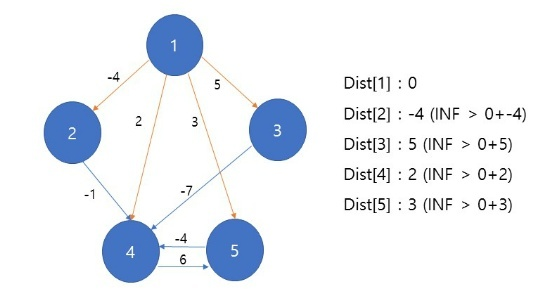
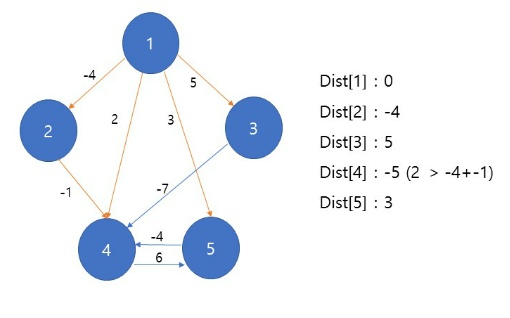
- 마찬가지로 다음 노드에서도 각각의 다른 정점까지의 거리를 구한다
그리고 갱신 조건이라면 거리를 업데이트한다
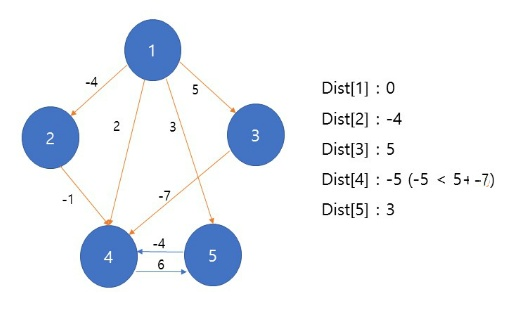
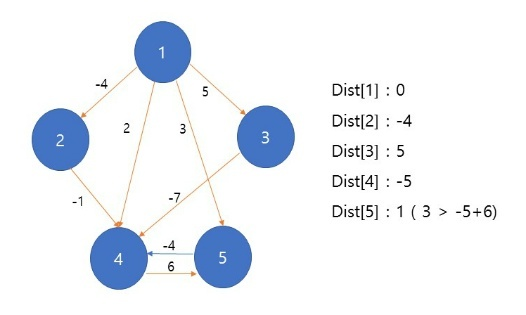
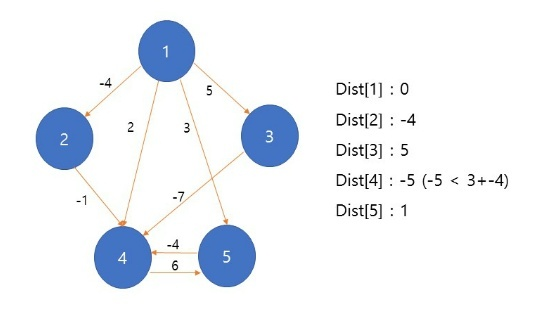
- 마지막 노드까지 탐색이 끝났다면 음의 사이클이 존재하는 지 확인해야한다
알고리즘에서 정점 n개 만큼 반복하는 과정을 한 번 더 진행한다. 이 때 바뀌는 값이 있다면 음수 사이클이 존재하는 것이다.
핵심 코드
백준 11657 번의 풀이과정 중 일부이다
//정점과 거리를 저장할 Edge 클래스가 필요하다
data class Edge(val from: Int, val to: Int, var cost: Long)
var graph = Vector<Edge>()
lateinit var dist : LongArray
fun bellmanFord ( start :Int) : Boolean{
dist[start] = 0
//N-1 번 , 즉 정점의 수 -1 번 실행한다
for(j in 1 until N){
// M : 간선의 수
for(k in 0 until M){
val cur = graph.get(k)
if(dist[cur.from]!=MAX ){
val cost = dist[cur.from] + cur.cost
if( cost < dist[cur.to] ){
dist[cur.to] = cost
}
}
}
}
//음수 가중치 확인
for (j in 0 until M){
//현재 간선의 들어오는 정점에 대해 비교 -> 더 작은 값 생기면 음수 사이클 존재
val cur = graph.get(j)
if(dist[cur.from]!= MAX && dist[cur.to] > dist[cur.from] +cur.cost){
return true
}
}
return false
}
fun solution () = with(System.`in`.bufferedReader()){
val st = StringTokenizer(readLine()," ")
N = st.nextToken().toInt()
M = st.nextToken().toInt()
dist = LongArray(N+1){MAX}
repeat(M){
val case = StringTokenizer(readLine(), " ")
val start = case.nextToken().toInt()
val end = case.nextToken().toInt()
val time = case.nextToken().toLong()
graph.add(Edge(start,end,time))
}
val result = bellmanFord(1)
}
