해시(Hash)

윤·2023년 8월 30일

algorithm hash

알고리즘

목록 보기

1/23

해시 함수(Hash Function), 해싱(Hashing)

임의의 길이를 갖는 임의의 데이터를 고정된 길이의 데이터로 매핑하는 단방향 함수를 해시 함수라고 한다.

매핑 전 원래 데이터 값을 키(key), 해시 함수를 적용하여 나온 고정된 길이의 값을 해시값(hash value), 해시 코드, 해시섬(sum), 체크섬 등으로 부른다.

키(key)를 해시값(hash value)로 변환하는 과정을 해싱(Hashing)이라고 한다.

해시 테이블(Hash Table)

해시 테이블(Hash Table)은 key와 value가 하나의 쌍을 이루는 데이터 구조이다. 해시 함수를 사용해 키를 해시 값으로 변환하고, 이 해시 값을 인덱스로 삼아 키와 데이터를 저장하는 자료구조를 말한다. 기본 연산으로는 탐색(Search), 삽입(Insert), 삭제(Delete)가 있다.

해시 충돌(Hash Collision)

해시 충돌이란 해시 함수가 서로 다른 두 개의 입력값(key)값에 대해 동일한 출력값(value)를 내는 상황을 의미한다.

충돌이 많아질수록 탐색의 시간 복잡도가 O(1)에서 점점 O(n)에 가까워지게 된다.
해결 방법은 크게 2가지가 있다.

개별 체이닝(Separating Chaining)
개방 주소법(Open Addressing)

개별 체이닝(Separating Chaining)

중복된 해시 값이 있는 경우, 연결 리스트(Linked List)로 만들어 저장한다.

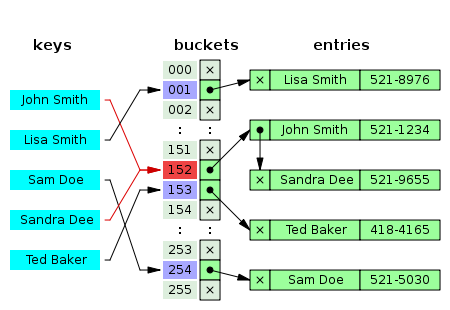
해시 충돌이 일어날 때, 인덱스가 가리키고 있는 Linked List에 노드를 추가해 값을 삽입한다.
데이터를 탐색할 때는 키에 대한 인덱스가 가리키고 있는 Linked List를 선형 검색 하여 해당 키에 대한 데이터를 반환한다.
선형 검색을 해야하기 때문에 최악의 경우 수행 시간이 O(n)이 된다.
데이터를 삭제할 때는 인덱스가 가리키고 있는 연결 리스트에서 그 노드를 삭제한다.
Linked List 구조를 사용하기에 추가할 수 있는 데이터 수의 제약이 작다.

개방 주소법(Open Addressing)

개별 체이닝(Separating Chaining)은 데이터의 인덱스는 바뀌지 않는 Closed Addressing 기법이다.
반면 개방 주소법은 해시 충돌이 일어나면 비어있는 다른 인덱스를 찾아 데이터를 삽입한다. 추가적인 메모리 공간을 사용하지 않기 때문에 개별 체이닝(Separating Chaining) 방식에 비해 메모리를 덜 사용한다.

인덱스를 선택하는 로직으로는 대표적으로 3가지가 있다.

선형 탐색(Linear Probing) : 해시 충돌 시 다음 인덱스, 혹은 몇 칸 뒤 인덱스에 데이터 삽입
제곱 탐색(Quadratic Probing) : 해시 충돌 시 제곱 만큼 건너 뛰어 인덱스에 데이터 삽입
이중 해시(Double Hashing) : 해시 충돌 시 다른 해시 함수를 한 번 더 적용한 해시코드 이용

선형 탐색(Linear Probing) 사용

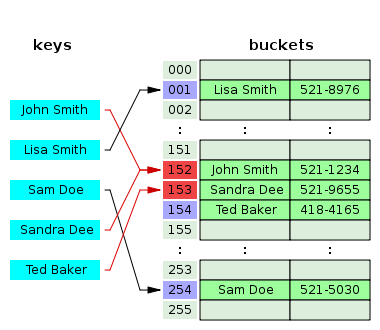
해시 충돌이 발생할 때 인덱스 뒤에 있는 버킷 중 빈 버킷을 찾아 데이터를 삽입한다.
그림에서 Sandra의 키 값의 인덱스는 152를 가리키지만, John과 충돌이 나기 때문에 비어있는 그 다음 인덱스인 153에 삽입한다.
Linear Probing 방식에서 탐색은 Sandra의 키에 대해 검색을 하면 인덱스가 152이기 때문에, 키가 일치하지 않는다. 따라서 뒤의 인덱스를 검색해서 같은 키가 나오거나 키가 없을 때까지 검색을 진행한다.
삭제가 어렵다는 단점이 있다.