코딩테스트는 취업 시 중요한 부분이다. 많은 회사에서 면접을 볼 때 코딩테스트를 통해 지원자의 개발능력을 가늠한다. 물론 코딩테스트를 잘하고 못하고가 개발에 직접적인 관련이 있지는 않지만 면접관님들의 입장에서는 가장 빠르게 실력을 가늠할 수 있는 부분이다보니 꽤나 중요하게 여겨야할듯싶다.
최근 알고리즘,자료구조를 공부하는데 너무 어려워서 큰 벽에 막힌것만같은 느낌이었다. 하지만 그래도 꿋꿋이 노력하며 공부하려고한다. 비록 잠시 뒤쳐지더라도 나중엔 같은 선에 서있을수있도록 미래를 위해 공부할 계획이다. 그럼 오늘도 공부 시작!!😆

---

학습목표
1.알고리즘이 무엇인지 설명할 수 있다.
2.알고리즘 문제를 이해하고 전략을 세울 수 있다.
3.알고리즘 풀이에 필요한 의사코드를 작성할 수 있다.
4.의사코드에서 세운 전략을 코드로 구현할 수 있다.
5.내가 구현한 알고리즘을 자바언어로 설명할 수 있다.

---

알고리즘이란?

알고리즘은 문제를 해결하는 최선의 선택이다.

문제를 풀기 위해서는 이 순서를 거쳐야한다.

• 문제를 이해하기
• 문제 해결 전략 세우기
  • 수도코드(의사코드) 작성 중요!
• 문제를 코드로 옮기기

여기서 수도코드가 굉장히 중요하다.

의사코드 (pseudocode)

의사코드는 수도코드, 슈도코드 등으로도 불리는데, 프로그래밍 언어로 코드를 작성하기 전, 사람의 언어로 프로그램이 작동하는 논리를 먼저 작성하는걸 말한다.

의사코드를 작성하게된다면 생기는 장점들도 다양하다.
1.시간 단축
2.디버깅 용이
3.프로그래밍언어를 모르는 사람과도 소통 가능

컴퓨터는 사람과 달리 상상력이 없기 때문에 어떤 행동을 지시할 때 굉장히 기초적인 부분부터 상세히 명령해야한다. 그렇기에 의사코드를 작성할때 구체적으로 작성해야 어떤 코드를 작성해야할지 쉽게 구분하고 알 수 있어 중요하다.

시간 복잡도 (Timme Complexity)

시간복잡도란 입력값의 변화에 따라 연산 실행시 걸리는 시간을 말하는데, 알고리즘의 로직을 구현할 때 시간복잡도를 고려해야한다.
시간복잡도는 Big-O, Big-Ω, Big-θ 를 사용하는데 주로 빅-오(Big-O) 표기법을 사용한다.

Big-O 표기법

빅오 표기법은 최악의 경우를 고려하기때문에 프로그램 실행시 최악의 시간까지 고려할 수 있다.

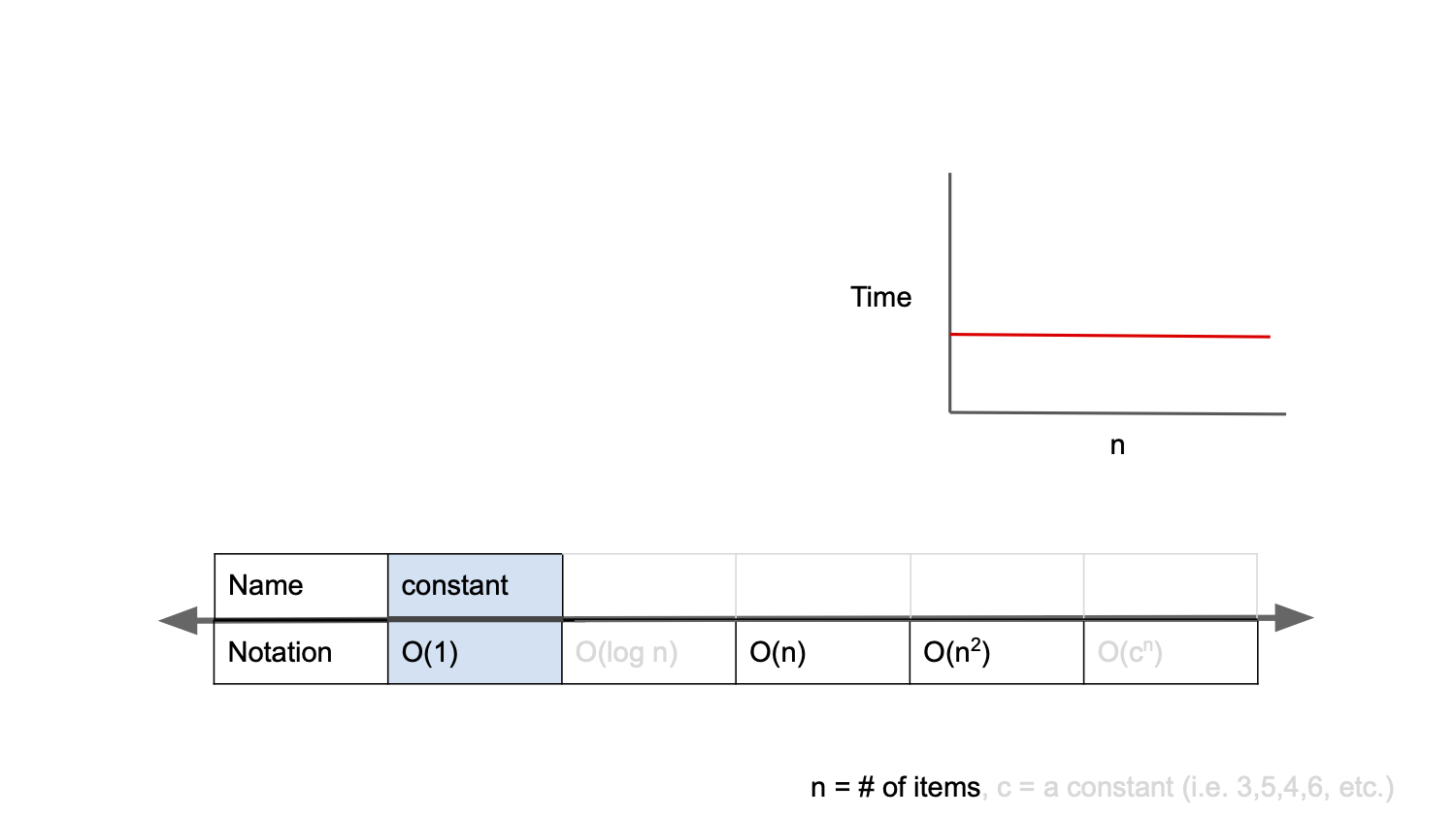
• O(1)
  시간복잡도가 O(1)인 경우, constant complexity라고 하며 입력값이 증가하더라도 시간이 늘어나지 않는다.
  즉, 입력값의 크기와 상관없이 즉시 출력값을 얻어낼 수 있다는 의미이다.

• O(n)
  시간복잡도가 O(n)인 경우, linear complexity라고 하고, 입력값이 증가함에 따라 같은 비율로 증가한다.
  즉, 입력값이 1일때 1초가 걸린다고 하면 입력값을 100배로 증가시켰을때 걸리는 시간도 100초가 걸린다고 할 수 있다.

• O(log n)
  시간복잡도가 O(log n)인 경우, logarithmic complexity라고 하며 Big-O 표기법 중 O(1) 다음으로 빠른 시간복잡도를 가진다.
  자료구조에서의 BST(Binary Search Tree)는 원하는 값을 탐색할 때, 노드를 이동할때마다 경우의 수가 절반으로 줄어든다.

  up & down 게임
  1.1~100 사이 숫자를 고른다. (ex 30)
  2.50을 제시하면 30은 50보다 작으므로 down
  3.이제 1~50사이의 숫자이므로 경우의 수를 낮추기 위해 25를 제시한다.
  4.25보다 크므로 up
  5.경우의 수를 계속 반으로 줄여나가며 답을 찾는다

위와 같이 경우의 수를 절반으로 줄이는 로직이 O(log n)의 시간복잡도를 가진 알고리즘이다.

• O(n2)
  시간복잡도가 O(n2)인 경우, quadratic complexity라고 하며 입력값이 증가함에 따라 시간이 n의 제곱으로 증가한다.
  즉 입력값이 1일 경우 1초가 걸리는 알고리즘에 5의 값을 주면 25초가 걸린다.

• O(2n)
  시간복잡도가 O(2n인 경우, exponential complexity라고 하며, Big-O 표기법 중 가장 느린 복잡도를 가진다.

  데이터 크기 제한	예상시간복잡도
  n <= 1,000,000	O(n) or O(lon n)
  n <= 10,000	O(n2)
  n <= 500	O(n3)

stack에서 찾을 수 있는 시간 복잡도

• 스택에 새로운 요소를 넣거나 뺄 때 발생하는 O(1)
• 스택을 탐색하는 O(n)

탐욕 알고리즘 (Greedy)

탐욕알고리즘은 말 그대로 선택할때마다 당장 눈앞에 있는 최적의 상황만 쫒아 답에 도달하는 방법이다.

탐욕 알고리즘으로 문제를 해결하는 방법
1. 선택절차(Selection Procedure) : 현재상태에서의 최적의 해답을 선택
2. 적절성 검사(Feasibility Check) : 선택한 답이 문제의 조건을 만족하는지 검사
3. 해답검사(Ssolution Check) : 원래의 문제가 해결되었는지 검사하고 해결되지않았다면 처음으로 돌아가 반복

탐욕 알고리즘을 적용하려면 해결하려는 문제가 2가지 조건을 달성해야함
1. 탐욕적 선택속성(Greedy Choice Property) : 앞의 선택이 이후에 영향을 주지 않는다
2. 최적 부분 구조(Optimal Substucture) : 문제에 대한 최종 해결 방법은 부분 문제에 대한 최적 문제 해결방법으로 구성

구현(Implementation) - 시뮬레이션(Simulation)

본인이 선택한 프로그래밍언어의 문법을 정확히 알고있어야하며, 문제의 조건에 전부 부합하는 코드를 실수없이 빠르게 작성하는 것을 목표로 두는 것을 구현문제, 구현유형이라고 한다.

구현 능력을 보는 대표 사례는 완전 탐색(brute force)과 시뮬레이션(simulation)이 있다.

시뮬레이션

시뮬레이션은 모든 과정과 조건이 제시되어 그 과정을 거친 결과가 무엇인지 확인하는 유형.
문제에 대한 이해를 바탕으로 제시하는 조건을 하나도 빠짐없이 처리해야 정답

완전 탐색 알고리즘(Brute-Force Algorithm)

Brute Force는 시행착오 방법론을 말한다.

Brute Force Algorithm, BFA는 무차별 대입 방법을 나타내는 알고리즘이다.
순수히 컴퓨터성능에 의존하여 모든 가능성을 시도하여 문제를 해결하는 방법.
즉, 최적의 방법이 아닌 공간복잡도와 시간복잡도를 고려하지 않고 최악의 방법이더라도 해결법을 찾는것이다.

Brute Force Algorithm은 크게 두 경우에 사용한다.
1. 프로세스 속도를 높이는데 사용할 수 있는 다른 알고리즘이 없을때
2. 문제를 해결하는 여러 방법이 있고 각 방법을 확인할때

완전탐색알고리즘은 문제에 더 적절한 해결법을 찾기 전에 시도하는 방법이지만 데이터의 범위가 커질수록 비효율적이다.
프로젝트의 규모가 커진다면 더 효율적인 알고리즘을 사용해야한다.

완전 탐색 알고리즘 단점

• 문제가 복잡해질수록 기하급수적으로 많은 자원을 필요로하는 비효율적 알고리즘이 될 수 있다.

완전탐색 알고리즘 사용

• 순차검색 알고리즘(Sequential Search)
  • 배열안에 특정값이 존재하는지 검색할 때 인덱스 0부터 마지막 인덱스까지 검색
  • 반복문을 통해 범위를 줄이지 않고 하나하나 비교하는것
  • BFS, DFS는 그래프 자료 구조에서 모든 정점을 탐색하기 위한 방법이다.
• 문열매칭 알고리즘(Brute-Force String Matching)
  • 길이가 n인 전체 문자열과 길이가 m인 문자열의 패턴을 포함하는지 검색
• 선택정렬 알고리즘(Selection Sort)
  • 전체 배열을 검색하여 현재 요소와 비교하고 컬렉션이 완전히 정렬될때까지 현재 요소보다 더 작거나 큰 요소(오름차순 또는 내림차순) 를 교환하는 정렬 알고리즘
• 버블정렬 알고리즘(Bubble Sort)
  • 서로 인접한 두 원소를 검사하여 정렬하는 알고리즘
  • 선택정렬과 기본개념 비슷
  • 정렬과정에서 원소의 이동이 거품이 수면위로 올라오는것과 비슷하기에 버블이라는 이름이 붙음
  • 선택정렬과 달리 안정정렬이다.
• Dynamic Programming
  • 큰 문제를 작은 문제로 나누어 푸는 것을 동적 프로그래밍(다이나믹 프로그래밍)이라고 한다.
  • 조건
    1. 작은 문제가 반복이 일어나는 경우
    2. 같은 문제는 구할때마다 정답이 같다
• DP와 BruteForce의 차이점
  • DP는 Brute Force를 개선시킬 수 있다.
  • 둘의 큰 차이점 중 하나는 어떤 경로나 수를 탐색했을때 값을 저장해주는 공간이 존재여부이다. (DP가 갖고있다.)
  • 값 저장 공간은 이미 찾은 경로를 재탐색하지않기 위해 필요하다.

이진 탐색 알고리즘(Binary Search Algorithm)

탐색알고리즘은 크게 3가지가 있는데 Linear Search Algorithm(선형 탐색 알고리즘), Binary Search Algorithm(이진 탐색 알고리즘), Hash Search Algorithm(해시 탐색 알고리즘)이 있다.

이진 탐색 알고리즘은 데이터가 정렬된 상태에서 절반씩 범위를 나눠 분할 저복기법으로 특정한 값을 찾아내는 알고리즘이다.

이진탐색알고리즘 동작
1. 정렬된 배열의 가장 중간 인덱스 지정
2. 찾으려는 값이 지정한 중간 인덱스의 값이라면 탐색 종료, 아니라면 3단계
3. 찾으려는 값이 중간인덱스보다 큰지 작은지 확인
4. 값이 있는부분과 없는 부분으로 분리
5. 값이 있는 부분에서 1단계부터 반복

이진탐색알고리즘 주 사용

• 정렬된 배열에서 요소값을 효율적으로 검색할때
• 데이터의 양이 많으면 많을수록 효율이 높아져 정렬된 데이터의 양이 많을때 사용
• 사전검색, 도서관 도서 검색, 대규모 시스템 리소스 사항 파악 등

이진탐색알고리즘 한계

• 배열에서만 구현 가능
• 정렬되어있어야만 구현 가능

Binary Search Tree : 자료구조
Binary Search Algorithm : 해결방법