[알고리즘] 이진 검색(Binary Search)

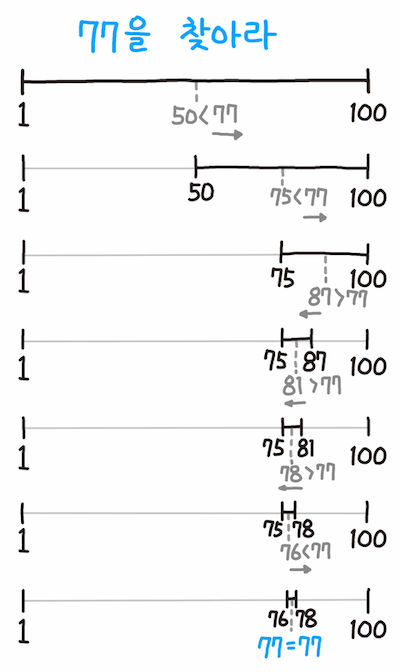
이진 검색(Binary Search)이란, 정렬된 데이터에서 검색 범위를 절반씩 줄여나가면서 원하는 값을 검색하는 알고리즘이다.
정렬된 데이터의 중간에 위치한 값과 찾으려는 값의 크기를 비교함으로써 검색 범위를 좁혀가게 된다.

이진 검색은 분할 정복(Divied and Conquer) 알고리즘 중 하나로, 이진 검색은 사전에서 단어를 찾을 때를 떠올리면 이해가 쉽다.
사전을 펴서 찾는 단어가 없으면 위치에 따라 앞쪽을 찾거나 뒤쪽을 찾고, 찾을 때까지 반복하는 행위가 이진 검색의 핵심 원리이다.

검색 범위를 절반씩 줄여나가기 때문에 log N번의 비교 연산을 통해 데이터에서 값을 검색할 수 있다.

구현 [Python]

1. 반복문

def binary_search(a: List[int], target: int) -> int:
    lo, hi = 0, len(a) - 1

    while lo <= hi:
        mid = (lo + hi) // 2
        if a[mid] < target:
            lo = mid + 1
        elif target < a[mid]:
            hi = mid - 1
        else:
            return mid  # found

    return -1  # not found.

2. 재귀

def binary_search(a: List[int], target: int, lo: int, hi: int) -> int:
    if hi < lo:
        return -1  # not found

    mid = (lo + hi) // 2
    if a[mid] < target:
        return binary_search(a, target, mid + 1, hi)
    elif a[mid] > target:
        return binary_search(a, target, lo, mid - 1)
    else:
        return mid  # found

구현 시 주의점

이진 검색을 구현할 때 주의해야 하는 것이 있다.

mid = (lo + hi) // 2

인덱스 mid를 계산할 때 오버플로우가 발생할 수 있다는 점이다.
lo + hi의 값이 int 자료형의 범위를 벗어날 수 있기 때문이다.

이는 아래와 같은 코드로 해결할 수 있다.

mid = lo + (hi - lo) // 2

파이썬의 경우 오버플로우가 발생해도 임의 정밀도 정수형을 지원하기 때문에 이 문제에서 자유롭다.
반면 C에서는 예상치 못한 임의의 결과를 반환하게 되고, Java에서는 오류가 발생한다.
따라서 자료형이 엄격한 언어로 이진 검색을 구현할 시 주의가 필요하다.