Fisher Information

통계학에서 Fisher Information이란,
: 관측 가능한 확률 변수 X가 X를 모델링하는 분포의 unknown parameter θ에 대해 가지고 있는 정보의 양을 측정하는 방법

MLE는 주로 asymptotically Gaussian이다.

여기서, MLE의 분산을 표현하기 위해서 Fisher Information을 정의할 필요가 있다.

Score function

Fisher Information을 정의하기 이전에, 먼저 score function을 정의할 필요가 있다.

Score function이란, 간단하게 말해서 log likelihood function의 도함수이다.

• i.e. $\theta$의 변동에 대한 likelihood function의 민감도

• $\mathbb{E}_\theta[s_\theta (X)]=0$
  • pf)

    pdf의 전구간 적분은 1이라는 것을 이용

Fisher 정보의 정의

Fisher information is just the variance of the score function, i.e.;

• $I(\theta)=Var[s_\theta(X)]=\mathbb{E}_\theta[s_\theta (X)^2]$

1. 로그 가능도 함수의 1차 및 2차 도함수를 이용한 정의:
   Fisher information은 $\ell (\theta)$의 2차 도함수의 기대값으로 정의
   $I(\theta) = -\mathbb{E}\left[\frac{\partial^2 \ell(\theta)}{\partial \theta^2}\right]$
   여기서 $\ell(\theta) = \log f(X; \theta)$는 확률 밀도 함수 $f(X; \theta)$에 로그를 취한 값.

2. 로그 가능도 함수의 1차 도함수를 이용한 정의:
   Fisher 정보는 로그 가능도 함수의 1차 도함수의 제곱의 기대값으로도 정의 가능
   

• 이는 위에서 언급한 $\mathbb{E}_\theta[s_\theta (X)]=0$ 성질을 이용한 결과
  

Fisher information의 의미와 중요성

1. Estimator의 분산과 효율성:
   Fisher information은 크래머-라오 하한(Cramér-Rao lower bound)과 밀접한 관련
   • 크래머-라오 하한은 unbiased estimator의 분산이 가질 수 있는 이론적인 lower bound를 제공하며, Fisher information을 이용해 다음과 같이 표현된다.
     $\text{Var}(\hat{\theta}) \geq \frac{1}{I(\theta)}$

• 즉, Fisher information이 클수록, 추정량의 분산이 작아져 더 효율적인 추정을 할 수 있게 됨

2. 정보량 측정:
   Fisher 정보는 데이터가 parameter에 대해 얼마나 많은 정보를 제공하는지를 측정
   - Fisher information이 크다는 것은 주어진 데이터가 parameter에 대해 많은 정보를 제공하여, 더 정밀하게 parameter를 추정할 수 있음을 의미

3. MLE와의 관계:

   Fisher information은 MLE에서 중요한 역할

   • MLE는 대체로 큰 sample size에서 효율적인 추정량이 되며, 이는 Fisher information을 통해 설명할 수 있다

   → MLE의 분산은 Fisher information의 역수에 근접하게 됨
   

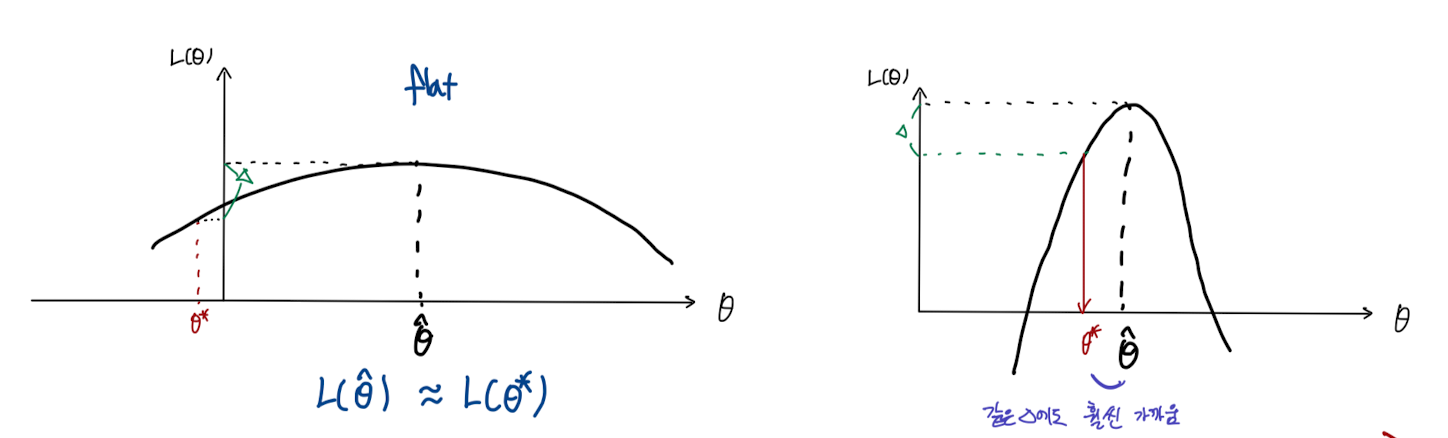
- (이 이미지의 의미 추가 예정)

요약

Fisher information은 parameter를 추정하는 데 있어서 데이터가 제공하는 정보의 양을 나타내며, estimator의 분산을 최소화하고 estimation의 정확성을 높이는 데 중요한 역할을 한다.

이를 통해 Fisher information은 통계적 추정의 efficiency를 평가하고 개선하는 데 유용한 도구로 사용된다.