BFS

BFS (너비 우선 탐색)

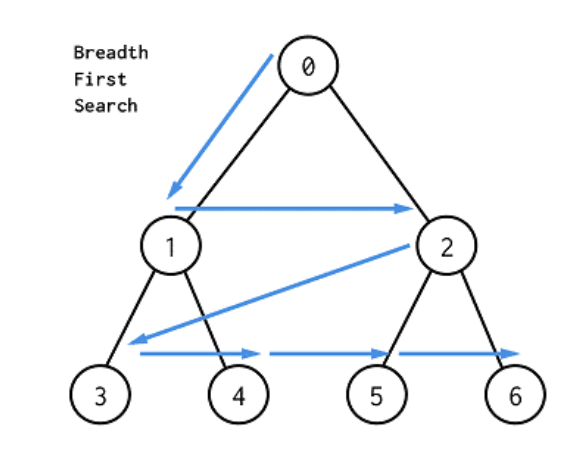
• 대표적인 그래프 탐색 알고리즘
• 정점들과 같은 레벨에 이는 노드들을 먼저 탐색하는 방식

HashMap으로 그래프 나타내기

HashMap<String, List<String>> graph = new HashMap<String, List<String>>();

graph.put("0", new ArrayList<String>(Arrays.asList("1","2");
graph.put("1", new ArrayList<String>(Arrays.asList("0","3");
graph.put("2", new ArrayList<String>(Arrays.asList("0","6");
graph.put("3", new ArrayList<String>(Arrays.asList("1");
graph.put("4", new ArrayList<String>(Arrays.asList("1");
graph.put("5", new ArrayList<String>(Arrays.asList("2");
graph.put("6", new ArrayList<String>(Arrays.asList("2");

BFS 과정

needVisit, visited 두 개의 큐를 사용한다.

visited
needVisit	0

---

visited	0
needVisit	1	2

---

visited	0	1
needVisit	2	0	3	4

---

visited	0	1	2
needVisit	0	3	4	0	5	6

---

visited	0	1	2	3
needVisit	4	0	5	6	1

---

visited	0	1	2	3	4
needVisit	0	5	6	1	1

---

visited	0	1	2	3	5
needVisit	6	1	1	2

---

visited	0	1	2	3	5	6
needVisit	1	1	2	2

예제

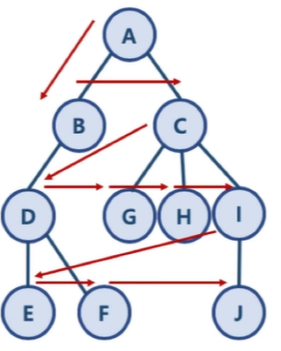
예제 코드

    public Queue<String> solution(HashMap<String, List<String>> graph, String startNode) {
        Queue<String> visited = new LinkedList<>();
        Queue<String> needVisit = new LinkedList<>();

        needVisit.add(startNode);

        while (needVisit.size() > 0) {
            final String node = needVisit.poll();

            if (!visited.contains(node)) {
                visited.add(node);
                needVisit.addAll(graph.get(node));
            }
        }
        return visited;
    }

    public static void main(String[] args) {
        final BfsExam T = new BfsExam();
        HashMap<String, List<String>> graph = new HashMap<>();
        graph.put("A", new ArrayList<>(Arrays.asList("B", "C")));
        graph.put("B", new ArrayList<>(Arrays.asList("A", "D")));
        graph.put("C", new ArrayList<>(Arrays.asList("A", "G", "H", "I")));
        graph.put("D", new ArrayList<>(Arrays.asList("B", "E", "F")));
        graph.put("E", new ArrayList<>(Arrays.asList("D")));
        graph.put("F", new ArrayList<>(Arrays.asList("D")));
        graph.put("G", new ArrayList<>(Arrays.asList("C")));
        graph.put("H", new ArrayList<>(Arrays.asList("C")));
        graph.put("I", new ArrayList<>(Arrays.asList("C","J")));
        graph.put("J", new ArrayList<>(Arrays.asList("I")));

        System.out.println(T.solution(graph, "A").toString());
    }

• 시간 복잡도
  • 노드 수 : V
  • 간선 수 : E
    = O(V + E)