순열, 조합, 중복순열, 중복조합

순열

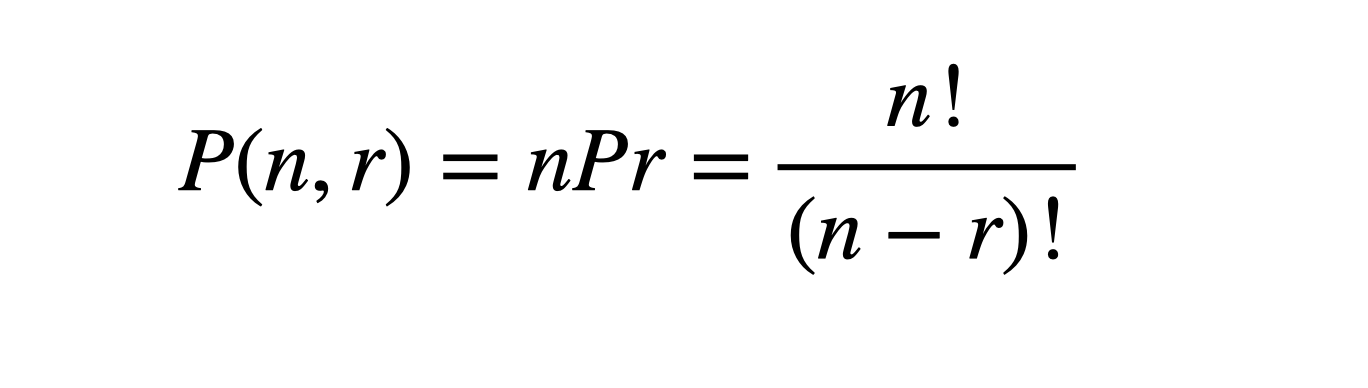
• 서로 다른 n개에서 r개를 택하여 순서를 고려하여 일렬로 나열하는 경우의 수

# (예시) A, B, C, D 4명의 후보가 있다. 이 중 3명을 순서대로 배치하여 팀장을 정하고 싶다면?

팀장을 선택할 경우:
1번째 자리: A, B, C, D → 4명 선택 가능
2번째 자리: A가 팀장인 경우 B, C, D 중 선택 → 3명 선택 가능
3번째 자리: 2번째가 B라면 C, D 중 선택 → 2명 선택 가능

따라서 이는 4 x 3 x 2 = 24가지 경우의 수
4P3 = 4 x 3 x 2 = 24

• (방법1) 재귀적으로 순열 구현

def permutations_recursive(arr, r):
    result = []  # 결과를 저장할 리스트

    def permute(current, remaining):
        """
        현재 원소를 선택하고 나머지 원소로부터 재귀 호출 
        current: 현재까지 선택한 원소 리스트
        remaining: 선택할 수 있는 남은 원소 리스트
        """
        if len(current) == r:  # 원하는 길이(r)에 도달하면 결과에 추가
            result.append(current)
            return
        for i in range(len(remaining)):  # 남은 원소들로 순열 생성
            # 현재 선택한 원소 추가하고, 남은 원소 중 i번째를 제외한 리스트를 전달
            permute(current + [remaining[i]], remaining[:i] + remaining[i+1:])

    permute([], arr)  # 순열 생성 시작
    return result

# 사용 예시
data = [1, 2, 3]
r = 2
print(permutations_recursive(data, r))  # [[1, 2], [1, 3], [2, 1], [2, 3], [3, 1], [3, 2]]

• (방법2) itertools.permutations

from itertools import permutations

# itertools.permutations를 사용하여 순열 생성
data = [1, 2, 3]
r = 2
result = list(permutations(data, r))  # 순열을 리스트로 변환
print(result)  # [(1, 2), (1, 3), (2, 1), (2, 3), (3, 1), (3, 2)]

조합

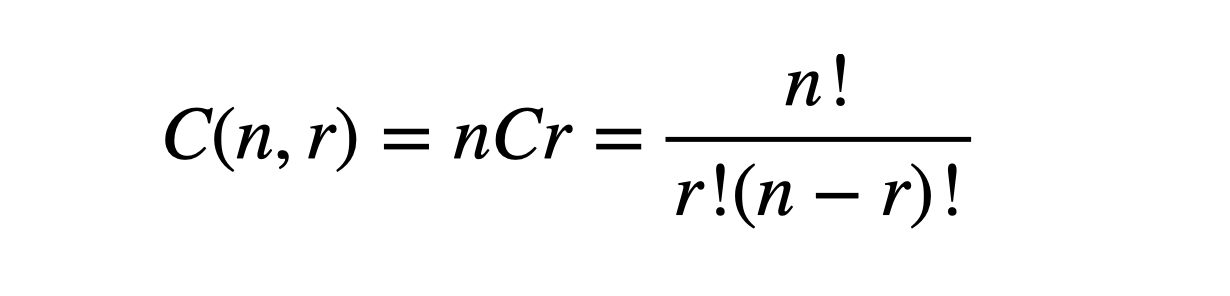
• 서로 다른 n개에서 순서를 고려하지 않고 r개를 택하는 경우의 수

# (예시) A, B, C, D, E 5명의 친구가 있다. 이 중 2명을 선택하여 영화를 보러 가려면?

(A, B), (A, C), (A, D), (A, E)
(B, C), (B, D), (B, E)
(C, D), (C, E)
(D, E)

따라서 이는 5C2 = 10가지 경우의 수
5C2 = 5P2 / 2! = (5 x 4) / (2 x 1) = 10

• (방법1) 재귀적으로 조합 구현하는 법

def combinations_recursive(arr, r):
    result = []  # 결과를 저장할 리스트

    def combine(current, start):
        """
        현재 원소를 선택한 후 다음 인덱스부터 탐색
        current: 현재까지 선택한 원소 리스트
        start: 탐색을 시작할 인덱스
        """
        if len(current) == r:  # 원하는 길이(r)에 도달하면 결과에 추가
            result.append(current)
            return
        for i in range(start, len(arr)):  # start부터 시작하여 조합 생성
            # 현재 선택한 원소 추가하고, 다음 인덱스부터 탐색
            combine(current + [arr[i]], i + 1)

    combine([], 0)  # 조합 생성 시작
    return result

# 사용 예시
data = [1, 2, 3]
r = 2
print(combinations_recursive(data, r))  # [[1, 2], [1, 3], [2, 3]]

• (방법2) itertools.combinations

from itertools import combinations

# itertools.combinations를 사용하여 조합 생성
data = [1, 2, 3]
r = 2
result = list(combinations(data, r))  # 조합을 리스트로 변환
print(result)  # [(1, 2), (1, 3), (2, 3)]

중복순열

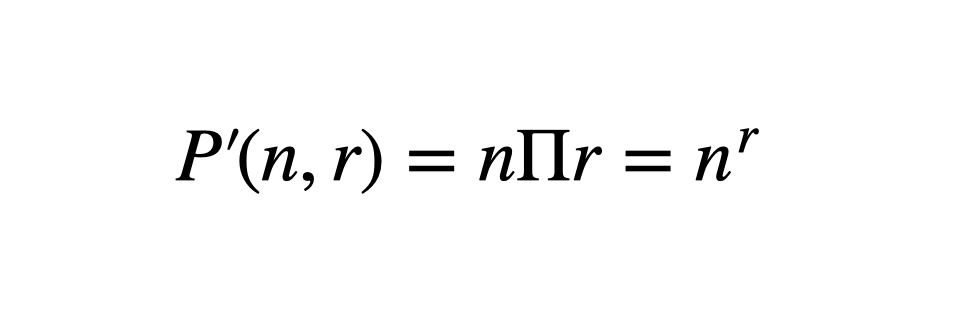
• 중복순열은 순열과는 다르게 같은 숫자를 중복하여 사용할 수 있음
• 중복을 허용하여 n개에서 r개를 선택하여 순서를 고려한 경우의 수

# (예시) 1,2,3,4,5가 적혀 있는 숫자 카드가 있다. 이를 중복을 허용해 세 자리 수를 만들 수 있는 방법은?

백의 자리에 올 수 있는 경우의 수: 5
십의 자리에 올 수 있는 경우의 수: 5
일의 자리에 올 수 있는 경우의 수: 5

백의 자리에 1이 올 때, 십의 자리에 올 수 있는 경우의 수는 1,2,3,4,5로 5가지이다. 이는 백의 자리에 2,3,4,5가 올 때도 동일하다. 따라서 이는 5x5x5로 5^3이 된다.

결론적으로, 서로 다른 숫자 5개 중에서 중복을 허용해 3개를 택하여 일렬로 배열한 경우의 수로
5π3 = 5x5x5 = 125

• (방법1) 재귀적으로 중복순열 구현

def product_recursive(arr, r):
    result = []  # 결과를 저장할 리스트

    def product(current):
        """
        현재 선택한 원소로 중복 순열 생성
        current: 현재까지 선택한 원소 리스트
        """
        if len(current) == r:  # 원하는 길이(r)에 도달하면 결과에 추가
            result.append(current)
            return
        for i in range(len(arr)):  # 모든 원소를 반복하여 중복 허용
            product(current + [arr[i]])

    product([])  # 중복 순열 생성 시작
    return result

# 사용 예시
data = [1, 2, 3]
r = 2
print(product_recursive(data, r))  
# [[1, 1], [1, 2], [1, 3], [2, 1], [2, 2], [2, 3], [3, 1], [3, 2], [3, 3]]

• (방법2) itertools.product

from itertools import product

# itertools.product를 사용하여 중복 순열 생성
data = [1, 2, 3]
r = 2
result = list(product(data, repeat=r))  # repeat=r로 중복 허용
print(result)  
# [(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)]

중복조합

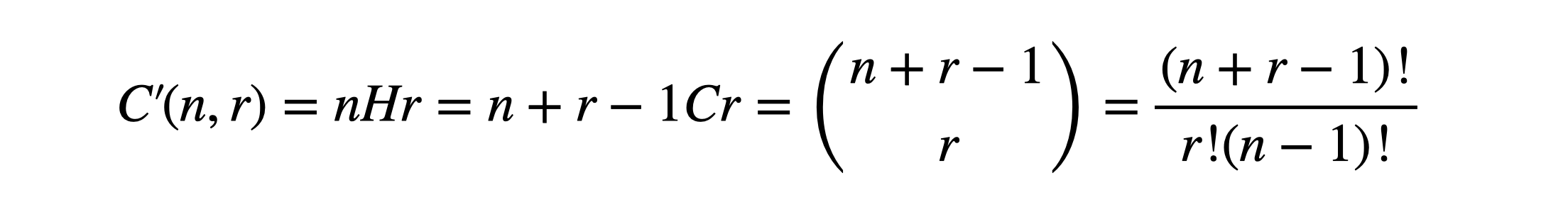
• 조합과는 다르게 같은 숫자를 중복하여 사용할 수 있음
• 중복을 허용하여 n개에서 순서를 고려하지 않고 r개를 택하는 경우의 수

# (예시) 1, 2, 3, 4 중에서 3개의 공을 뽑아 순서에 상관없이 조합을 만들 때?

(1, 1, 1), (1, 1, 2), (1, 1, 3), (1, 1, 4)
(1, 2, 2), (1, 2, 3), ... 
(3, 3, 3), (3, 3, 4), (4, 4, 4)

따라서 이는 중복조합 공식 nHr = (n + r - 1)Cr로 계산
4H3 = 6C3 = 6! / (3! x 3!) = 20가지 경우의 수

• (방법1) 재귀적으로 중복조합 구현

def combinations_with_replacement_recursive(arr, r):
    result = []  # 결과를 저장할 리스트

    def combine(current, start):
        """
        현재 선택한 원소로 중복 조합 생성
        current: 현재까지 선택한 원소 리스트
        start: 탐색을 시작할 인덱스
        """
        if len(current) == r:  # 원하는 길이(r)에 도달하면 결과에 추가
            result.append(current)
            return
        for i in range(start, len(arr)):  # 현재 위치부터 중복 조합 생성
            combine(current + [arr[i]], i)

    combine([], 0)  # 중복 조합 생성 시작
    return result

# 사용 예시
data = [1, 2, 3]
r = 2
print(combinations_with_replacement_recursive(data, r))  
# [[1, 1], [1, 2], [1, 3], [2, 2], [2, 3], [3, 3]]

• (방법2) itertools.combinations_with_replacement

from itertools import combinations_with_replacement

# itertools.combinations_with_replacement를 사용하여 중복 조합 생성
data = [1, 2, 3]
r = 2
result = list(combinations_with_replacement(data, r))  
print(result)  
# [(1, 1), (1, 2), (1, 3), (2, 2), (2, 3), (3, 3)]

* 요약

• 순열: 순서를 고려한 나열
• 조합: 순서를 고려하지 않은 선택
• 중복순열: 중복을 허용한 순서 고려 나열
• 중복조합: 중복을 허용한 순서 고려 없는 선택

---

참고

(1) [Python] Mutable vs. Immutable 차이점?
(2) [Python] 순열, 조합, 중복순열, 중복조합(itertools를 활용한 구현)
(3) 코딩테스트 준비할 때 필수 개념! <완전탐색> 알아보기