문제 링크 : https://leetcode.com/problems/shortest-palindrome
문제 해석
어떤 문자열 s가 주어진다. s의 앞부분에 최소한의 문자열을 붙여서 만들 수 있는 palindrome을 찾으라.
풀이
가장 긴 prefix palindrome을 찾고, 그 이후의 suffix를 반전하여 전체 문자열의 앞부분에 붙인다.
Two Pointer로 찾는 방법
s가 빈 문자열이 아닌 이상 Prefix palindrome이 늘 존재한다고 가정하자. 문자열의 길이가 1이라도 palindrome이라고 할 수 있기 때문에 그 가정은 타당하다. 그렇다면 다음의 절차를 1번 이상 반복하면 가장 긴 prefix palindrome을 찾을 수 있다. 맨 처음 n을 s의 길이와 동일하다고 설정한다.
left를 0으로 설정한다
right을 n-1으로 설정한다.
right을 -1하면서 이동하고, 만약 right의 위치에 있는 문자와 left의 위치에 있는 문자와 동일하다면 left를 +1한다.
n을 left로 설정한다.이 절차는 left가 n-1의 자리까지 옮겨갔을 때에 종료된다. 나는 왜 이걸 반복하면 결국 prefix palindrome이 찾아지는지를 이해하기가 어려웠는데, 다음과 같이 그림으로 그려보고 이해할 수 있었다.
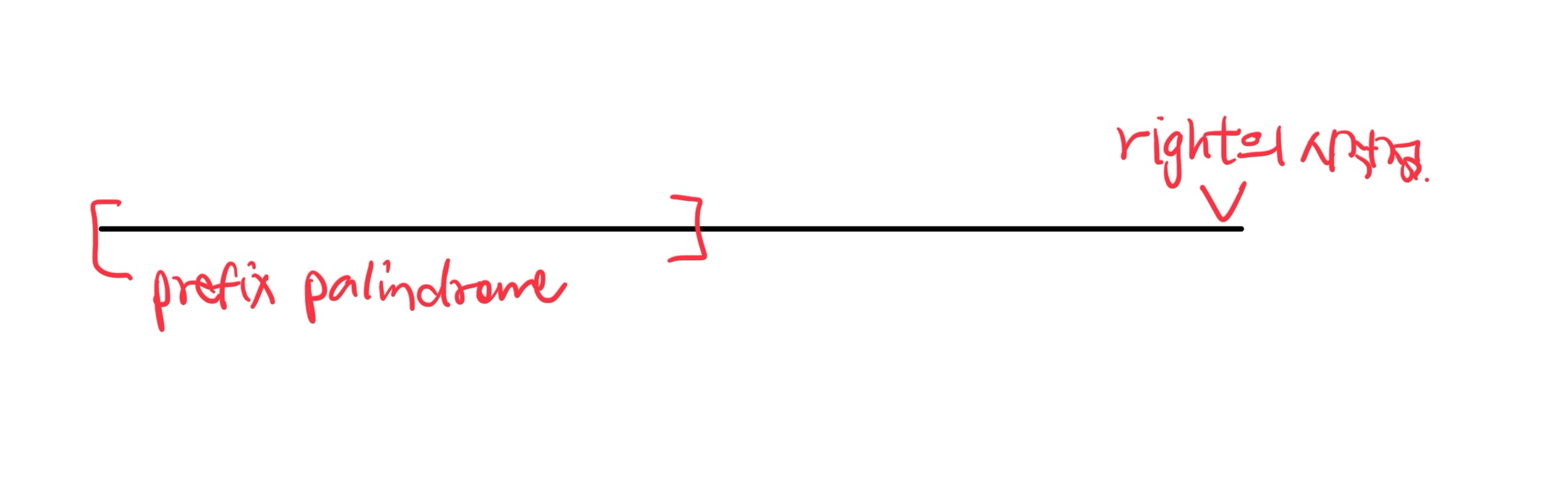
right은 늘 prefix palindrome보다 더 넓은 곳에서 시작해서 0으로 수렴하므로 prefix palindrome을 반드시 다 지나가게 된다. 만약 s에서 prefix palindrome을 제한 부분에서 right과 left가 동일한 지점이 발생한다면 .. 저 process가 끝날 때 left가 그 횟수만큼 오른쪽으로 밀려날 수도 있을 것이다. 저 process를 한 번 실행한다고 해서 반드시 prefix palindrome이 찾아진다고 보장할 수 없는 이유가 바로 그 때문이다. 그렇지만 prefix palindrome은 저 프로세스가 끝났을 때 [0, left)에는 포함되어 있다.
KMP 알고리즘으로 찾기
KMP 알고리즘은 어떤 문자열의 가장 큰 prefix이자 suffix인 부분을 찾는 알고리즘이다.
어떤 문자열에 대해 반복문을 돌면서 부분 문자열을 만들어내고,각 부분 문자열에 대해 suffix와 일치하는prefix의 길이를 그 이전의 값을 활용해서 계산하여, 이를 통해 어떤 문자열의 가장 큰 prefix이자 suffix인 부분을 찾는다.
이를 위해서 prefix function 혹은 partial match table을 만들어야 한다. 그 테이블의 i 인덱스에는 i에서 끝나는 부분 문자열에 관한 가장 긴 suffix이자 prefix의 길이가 담겨 있다. table[i]의 값은 length이며, s[:length]는 현재까지 계산해낸 최대 접두사(접미사와 동일)를 가리킨다. 이 length는 어떠한 prefix의 길이(현재까지 일치한 접두사와 접미사의 길이)이기도 하면서, array에서 사용하면 그 prefix의 바로 다음에 나오는 문자를 가리키는 인덱스가 되기도 한다.
문자열 s에 대해 반복문을 돌면서 다음의 process를 수행한다. 각 i는 매 iteration에서 substring의 끝부분에 해당한다.
-
끝부분(s[i])이 일치하면, prefix와 suffix의 길이를 하나 늘려서
partial match table에 기록한다. -
만약
현재 length를 가진 prefix의 바로 다음에 나오는 문자가, 현재 iteration의 substring의 끝부분과 일치하지 않는다면, 그 이전에 저장된 prefix의 length 값으로 업데이트 되어야 한다. 이를 보충설명해보자면 다음과 같다. 만약 일치하지 않으면, 현재 iteraion 이전에 한번이라도 발견된 적이 있는prefix이자 suffix이면서, 현재 prefix보다 작은 prefix를 찾아야 한다. 그런데 prefix보다 작은 prefix는 곧 prefix의 prefix이다. 그리고 그 prefix는 그냥 작기만 한 게 아니라prefix이자 suffix여야 한다. 현재 prefix가 부분 문자열로 설정되었던 iteration의 상황에서 계산되었던 (더 작은) prefix의 값을 찾으려면 현재 prefix의 Length-1을 인덱스로 하여partial match table에 인덱스 접근 하면 된다. 그리고 그 prefix의 다음 부분을 포함해서 만들어진 prefix가, 현재 iteration의 끝부분과 일치하는지를 확인하고, (1)이나 (2)를 length >0일 때까지, 그리고 i가 전체 문자열의 길이보다 작을 때까지 반복한다.

이런 KMP 알고리즘을 활용하여 문자열 s의 가장 긴 prefix palindrome을 찾을 수 있다.
문자열 s에서 s + "#" + reverse(s)라는 새로운 문자열을 만들고, 이에 대해 KMP 알고리즘을 활용하여 ‘prefix이자 suffix인 부분 문자열’을 계산한다면, palindrome을 계산할 수 있다. 새로운 문자열의 suffix에는 reverse(s)가 붙어 있으므로, prefix가 suffix와 일치한다면 곧 palindrome이라고 볼 수 있기 때문이다.
이 새로운 문자열에 대해 만들어진 partial match table의 각 element(=length)는 다음과 같은 성질을 가지고 있다. 원 문자열의 prefix(= s[:length])가 반전 무자열의 suffix(= s[length:])와 일치한다.
예를 들어, "aacecaaa" 문자열에 대해, 반전 문자열은 "aaacecaa"이다. 새로운 문자열은 "aacecaaa#aaacecaa". 여기서 찾아진 가장 긴 prefix이자 suffix인 부분 문자열은 "aacecaa" 이다. 이는 곧 가장 긴 prefix palindrome이다. 가장 긴 prefix palindrome을 찾고, 그 이후의 suffix를 반전하여 전체 문자열의 앞부분에 붙인다.
소감
KMP 알고리즘을 이해하는 데 거의 사흘이 걸렸다. 특히 length를 업데이트하는 부분이 잘 이해가 되지 않았는데, “prefix보다 작은 prefix는 곧 prefix의 prefix”라는 걸 알게 되니 이해가 되었다. 힘들게 이해한 만큼 다음에 만나게 된다면 꼭 직접 구현해서 문제를 풀어보고 싶다.
