문제 소개
'Minimum Height Trees' 문제는 2024년 4월 23일 Daily LeetCode Challenge 문제로 제시되었다. 사이클이 없는 그래프(트리)가 주어지는데, 그 중에서 어떤 노드를 루트로 만들었을 때 트리의 높이가 가장 낮아질 수 있을지를 물어보는 문제였다.
문제 풀이
1)brute-force
가장 심플한 방법으로는 모든 노드에 대해 각각 dfs나 bfs를 시작해서 방문되지 않은 노드가 없을 때까지 순회를 하고, 순회 종료 시점에서 스택의 길이 (재귀의 깊이) 혹은 너비를 구한 다음, 그 값이 가장 작을 때를 구하는 것이었다. 모든 n에 대해서 dfs를 반복하는 것은 시간초과를 낼 것이 분명했다.
2)또다른 방법 ← 시도
한 노드에서 다른 노드로 향하는 여러 path 중에서 가장 긴 path를 구하고, 그 path의 중간 노드(path의 길이가 홀수일 때 1개, 짝수일 때 2개)를 구하면 그것 곧 조건을 만족하는 루트라는 점에 착안해서 문제풀이를 시도했다. 그런데 결국 '한 노드에서 다른 노드로 향하는 여러 path 중에서 가장 긴 path를 구하는' 알고리즘은 '한 노드에서 다른 노드로 향하는 여러 path 중에서 가장 짧은 path를 구하는' 알고리즘과 동일한 brute-force 방식이었기 때문에 timeout이 날 수밖에 없었다.
오답 노트
'양파 껍질을 까는' 방식으로 리프 노드들을 바깥에서부터 하나씩 지워나간다면, 결국 마지막에 1~2개의 노드가 남게 되는데, 그것이 조건을 만족하는 루트가 될 것이다. 2개 이상의 노드가 있는 것은 곧 언제나 쳐낼 수 있는 하나 이상의 노드가 더 있다는 것을 뜻한다. '리프 노드를 구하는 것'을 단 한 번의 dfs 혹은 bfs를 통해서 한 다음, '리프 노드를 지우는 것'은 그렇게 구해진 값을 변형시키면서 할 수 있다면 brute-force보다 더 효율적인 알고리즘이 될 수 있다.
3) Editorial의 풀이 참고 시도
edges를 순회하면서 adjList를 생성한다. outgoing edge의 수가 한 개일 때 그 노드는 leaf라고 할 수 있다. 이 조건을 이용하여 adjList를 순회하면서 leaves 배열을 만들어낸다. '리프 노드를 구하는 것'은 이렇게 이루어진다. 만들어진 leaves 배열을 바탕으로 다시 adjList에 대해 '리프 노드를 지우는 것'을 한다. '리프 노드를 지우는 것'은 모든 adjList를 순회하면서, adjList에 만약 리프 노드를 담고 있으면 그것을 remove하는 방식으로 구성하였다. 그렇게 했을 때 n=20000일 때, 즉 worst-case에서 다시 timeout이 났다.
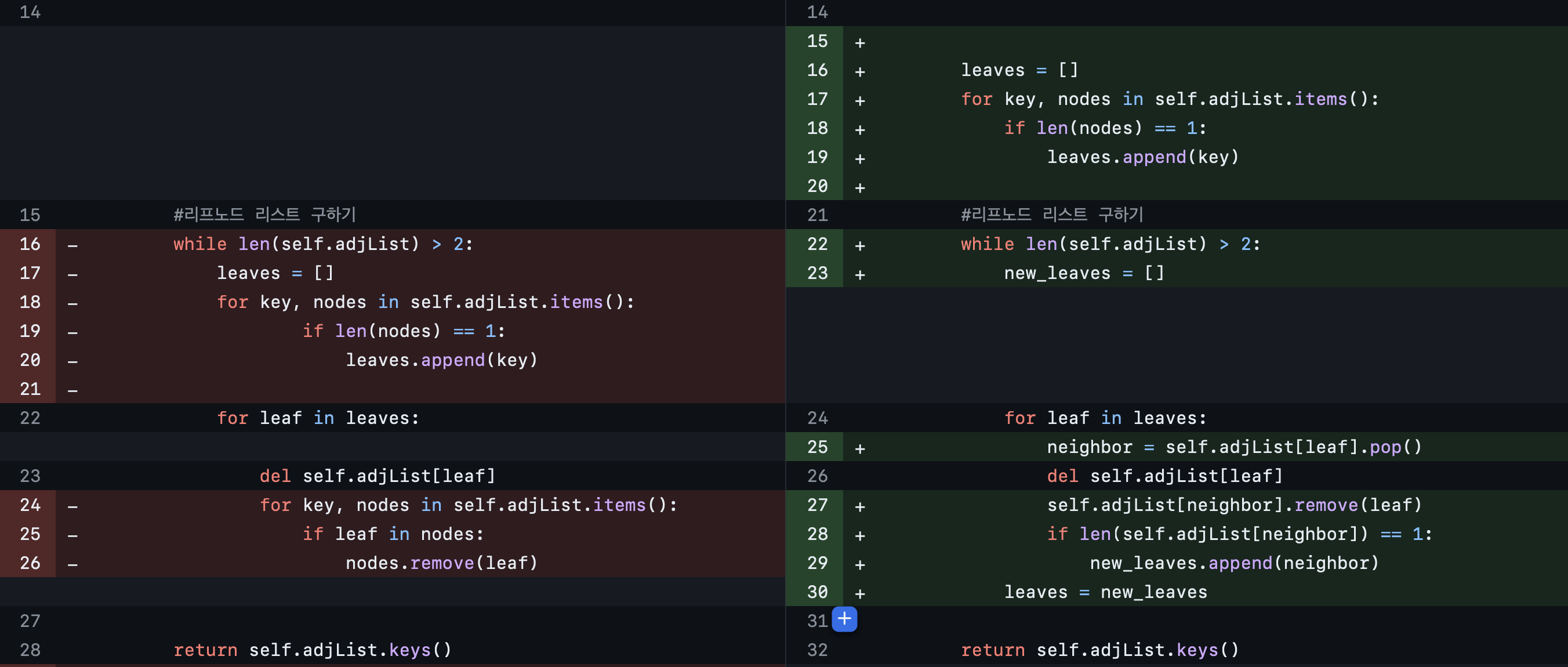
4) 마지막 시도
'지우는 연산'은 개선될 수 있었는데, 지울 대상을 찾는 과정의 시간복잡도를 개선할 수 있었기 때문이다. '리프 노드를 담고 있는 배열leaves'는 리프 노드의 유일 이웃 노드의 adjList이고, 유일한 이웃 노드를 키값으로 해서 그 이웃 노드의 adjList에 접근할 수 있었기 때문이다. 또한 '새로운 리프 노드를 찾는 것' 또한 개선될 수 있었는데, 이웃 노드의 adjList에서 리프 노드를 remove 하면, 변화된 adjList에 대해서만 다시 리프 노드의 조건을 만족하는지를 검사할 수 있고, 그 자리에서 바로 리프 노드의 새로운 배열을 만들 수도 있었다.
소감
트리의 특성과 속성에 대해서 조금 더 잘 알고 있었다면 더 쉽게 풀 수 있지 않았을까 생각이 든다. 특히 셋째 시도에서 adjList를 굳이 모두 순회했던 것은, "'리프 노드를 담고 있는 배열'은 리프 노드의 유일한 이웃 노드의 adjList"라는 것을 알지 못했기 때문이다. 또 모든 adjList를 순회하는 것이 timeout으로 이어질 수 있다는 점을 미처 생각하지 못했기 때문이기도 하다. 아직까지 time complexity에 대해서 감이 잘 오지 않는다. 좀 더 감이 잘 왔으면 좋겠다.
