python의 실수형 float를 다룰 때 흔히 마추지는 문제가 있다.
바로 float형끼리 연산에서 부동소수점 오차가 발생하는 점이다.

파이썬뿐만 아니라 거의 모든 프로그래밍 언어에서 동일하게 발생된 문제이다.

실수 표현 방식

그 이유는 컴퓨터는 모든 수를 0과 1로 이루어진 2진수로 표현한다. 이는 정수 뿐만 아니라 소수점이 존재하는 실수도 마찬가지이다. 실수를 표현하는 방식은 정수보다 복잡하지만 크게 2가지 방식이 있다.

1. 고정 소수점 (fixed point) 방식
2. 부동 소수좀 (floating point) 방식

그 중에서도 Python은 실수를 부동소수점으로 표현하는 방식을 따른다.

부동 소수점 (floating point) 방식

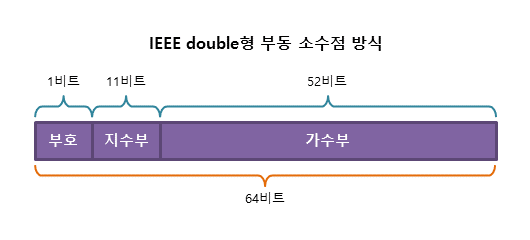
정수부 소수부로 나누는 고정소수점 방식과 다르게 부동 소수점 방식은 유효숫자를 나타내는 가수부와 소수점의 위치를 풀이하는 지수부로 나누어 표현한다.
부동 소수점 표현 방식은 수를 (가수 a)×(밑수 2)^(지수 b)와 같은 형태로 저장한다.
(a 는 1보다 크거나 같고, 2보다 작은 실수이다.)

부동 소수점 방식의 문제점 : 오차

부동 소수점 방식은 고정 소수점 방식보다 훨씬 더 많은 범위까지 표현할 수 있지만, 안타깝게도 십진 소수를 정확하게 이진 소수로 표현할 수가 없다.

분수 1/3을 생각해보면 아무리 많은 자릿수를 적어도 결과가 정확하게 1/3이 될 수 없지만, 점점 더 1/3에 가까운 근사치가 된다.

0.3

0.33

0.333...

마찬가지 방법으로 10진수 0.1을 이진법에서는 무한소수이기때문에 이진 소수로 정확하게 표현할수가 없다.

0.0001100110011001100110011001100110011001100110011...

무한 소수로 표현되게 되어 메모리 범위를 벗어나게 되므로 유한 한 비트 수에서 맞춰 근삿값을 얻게 됩다.
그래서 실제 수와 거의 같지만 정확하게 같지 않고 오차가 생겨나게 된다.

이처럼 컴퓨터에서 실수를 가지고 수행하는 모든 연산에는 언제나 작은 오차가 존재하게 된다.
이것은 파이썬뿐만 아니라, 모든 프로그래밍 언어에서 발생하는 기본적인 문제이다.

float형 부동 소수점 오차 해결방법

decimal.Decimal, math.fsum(), round(), float.as_integer_ratio(), math.is_close() 함수 혹은 다른 방법을 통해서 실수를 방지할 수 있다.
이 중 가장 추천하는 방법은 decimal 표준 라이브러리를 사용한 방법이고 그 외에도 존재하는 관련 함수들을 소개한다.
각 언어의 부동소수점 처리 방식을 볼 수 있는 https://0.30000000000000004.com/ 이란 사이트도 있다.

1. Decimal으로 정확한 자릿수 표현하기

반올림 오차가 없는 고정소수점을 사용하려면 decimal 모듈의 Decimal을 사용하면 된다. Decimal은 숫자를 10진수로 처리하여 정확한 소수점 자릿수를 표현한다.

from decimal import Decimal
Decimal('0.1') + Decimal('0.2')
Decimal('0.3')

2. Fraction으로 분수 표현하기

순환소수는 고정소수점이라도 정확히 표현할 수 없다. 이때는 fractions 모듈의 Fraction을 사용하여 분수로 표현한다.

from fractions import Fraction
Fraction('10/3')    # 10을 3으로 나누면 순환소수 3.33333...이지만 분수 3분의 10으로 표현
Fraction(10, 3)

3. 소수점 반올림 오차(rounding error)로 판별하기

실수를 근삿값으로 표현하면서 발생하는 문제를 부동소수점 반올림 오차(rounding error)라고 한다.
따라서 실수를 비교할 때는 연산한 값과 비교할 값의 차이를 구한 뒤 sys.float_info.epsilon보다 작거나 같은지 판단해야 한다.

import math, sys
x = 0.1 + 0.2
math.fabs(x - 0.3) <= sys.float_info.epsilon

정리

float 자료형을 다룰 땐 항상 부동소수점 오차를 신경써야 할 것 같다.
파이썬에서는 decimal 모듈을 주로 사용해야될것 같고 간단한 실수 계산에서는 round()같은 함수로 간단하게 처리해도 크게 문제는 없을 것 같다.