역추적 탐색(backtracking search)
∎ 전 단계로 탐색을 후진해서 다른 단서를 가지고 탐색을 시작하는 것(= 탐색 중 되돌아가는 것🔙)
∎ 사용 배경
대부분의 탐색 공간에서는 다른 상태로 이동하는 데 제약
그래프(graph), 연결 목록(linked list) 구조 데이터 👉 이동 제약⭕ 👉 역추적 탐색 사용
이동 제약❌ 👉 새로운 상태를 탐색하기 전, 바로 전 단계로 되돌아가는 것이 도움
*배열 구조 데이터 👉 인덱스로 쉽게 이동(알고리즘의 효율성👍)
너비 우선 탐색(breadth-first search)
∎ 마주친 순서대로 탐색 상태들을 살펴보는 알고리즘 (=선입선출 알고리즘)
이웃 상태를 폭넓게 살펴보는 탐색
∎ 탐색 단계마다 현재 노드가 목표 노드인지 아닌지를 검사
∎ 이웃 노드가 초면 or 구면 확인
💗장점 - 노드의 중복 확인 ❌
💔단점 - 큐 유지 메모리보다 더 큰 용량 필요 (for 확인한 노드 기록)
∎ 목표 노드 확인❌ 👉 목록에 추가한 적 없는 노드를 목록에 추가 (for 이미 살펴본 노드나, 이미 목록에 들어 있지만 아직 살펴보지 않은 노드를 목록에 추가하는 일을 방지)
∎ 각 노드에 연결된 이웃이 많을 때 👉 메모리 용량👆(for 큐 유지)
(대규모 탐색 문제에서는 메모리 용량을 필요한 만큼 늘리는데 비용이 많이 듦.)
∎ 너비 우선 탐색 특성
🤍 시작 노드에서 X만큼 떨어진 곳에 있는 노드를 모두 탐색한 뒤 X+1만큼 떨어진 노드들을 살펴보는 방식 👉 점점 바깥으로 확장
🤍 노드 이동 비용(시간, 에너지 등)이 모두 같은 경우 👉 탐색 비용을 최소화하는 경로
∎ 너비 우선 탐색 후방 포인터(back pointer)
너비 우선 탐색 조정 👉 직전에 검사한 노드를 기록하는 후방 포인터(back pointer) 👉 최단 거리
∎ 너비 우선 탐색으로 최단 거리를 구하는 방법
🤍 탐색 중 검사하는 노드마다 직전에 검사한 노드를 알려주는 후방 포인터 기록
🤍 목표 노드를 찾은 뒤에 후방 포인터를 따라 시작 지점까지 BACK 👉 최단 거리(시작 지점 ~ 목표 지점)
❗한 노드에서 이웃 노드로 이동하는 데 드는 비용이 모두 같을 때만 사용❗
*큐(queue): 이미 알고 있지만 아직 살펴보지 않은 상태를 목록 👉 너비 우선 탐색 시각화
목록에 없는 새로운 상태를 발견 👉 큐의 맨 뒤에 추가
cf. 그래프 탐색
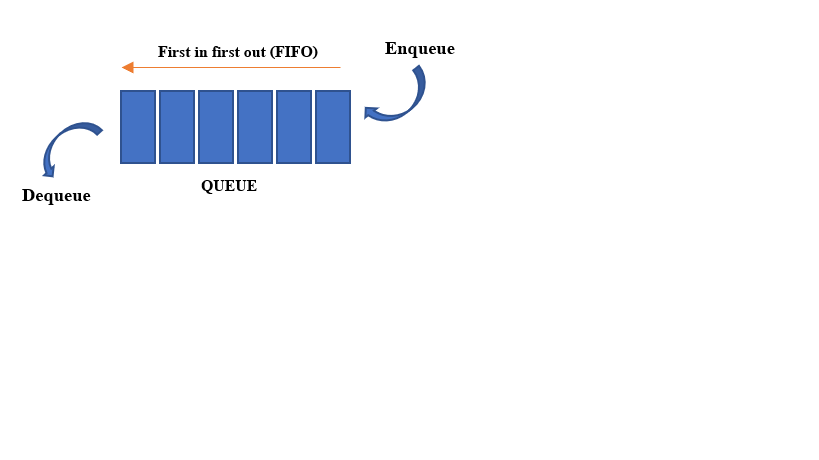
QUEUE(선입선출구조. FIFO구조)
*그래프: 독립된 여러 개의 노드(node) + 각 노드 사이를 잇는 간선(edge)으로 이루어진 자료구조.
연결된 두 노드는 서로의 이웃(neighbor)으로 이동⭕
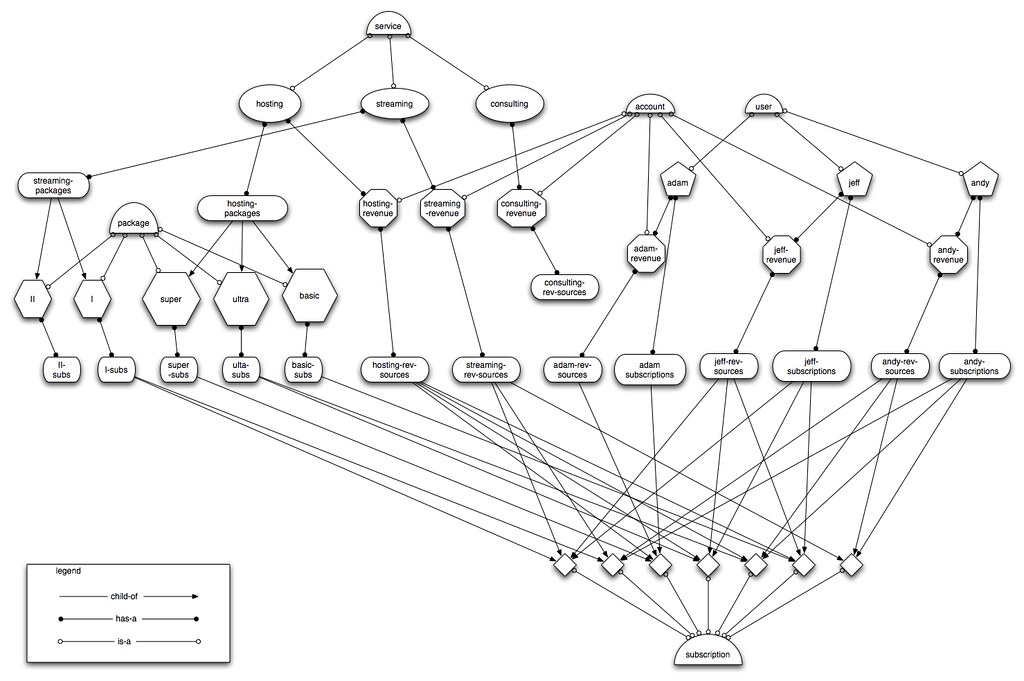
GRAPH STRUCTURE SAMPLE
∎ 너비 우선 탐색에서의 그래프 탐색 문제
📍 탐색대상: 그래프의 노드
📍 시작 노드에서 X만큼 떨어진 노드를 모두 확인
📍 X+1만큼 떨어진 노드를 확인 👉 경계를 확장
*최소 에너지 + 목표 지점 최단 거리 👉 효율적인 탐색
*탐색 공간에서 탐새 단계를 최소화(루트 최소화) ≠ 목표 노드까지의 경로에 대한 비용을 최소화(에너지 최소화)
cf. 도보 여행자의 루트
가까운 길 - 산길
덜 힘든 길 - 산길보다 거리가 긴 평지
깊이 우선 탐색(Depth-first search)
∎ 가장 나중에 마주친 탐색 상태부터 먼저 살펴보는 알고리즘(=후입선출 알고리즘)
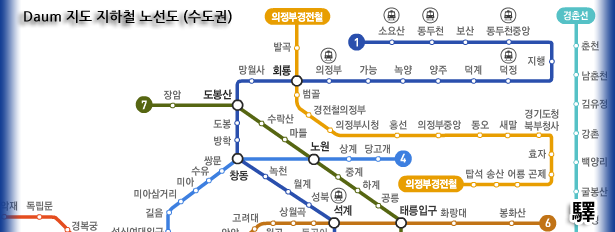
갈아타지 않고 한 노선의 지하철로 종점까지 탐색, 막다른 곳까지 쭉 내려가서 확인하는 탐색
∎ 목표 지점 또는 막다른 곳에 다다를 때까지 한 길을 따라 내려가며 탐색 진행
*스택(stack): 목록에 없는 새로운 상태 발견 👉 스택의 맨 위에 추가
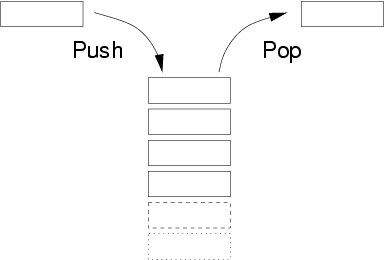
STACK(후입선출구조. LIFO구조) and push, pop
∎ 탐색 단계마다 스택의 맨 위에 있는 다음 상태로 진행
∎ 너비 우선 탐색 VS 깊이 우선 탐색
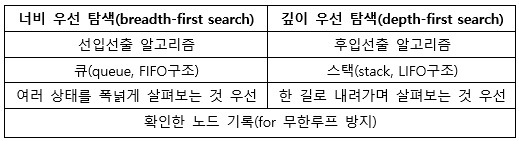❗ 탐색 경로도 차이가 있음 ❗
다음 포스팅💌 👉 [자료구조] stack🥀과 queue🌱
