탐색문제🧐
탐색문제 👉 알고리즘 + 자료구조 풀이
Algorithm
Data-structure
∎ 탐색 문제(search problem)
우리가 찾는 값일 가능성이 있는 값을 모두 모아 둔 공간(탐색 공간)에서 특정한 값(목표)🧐을 찾아내야 하는 문제
∎ 모든 알고리즘의 3가지 공통 구성 요소
[ 탐색목표 + 탐색 공간 + 탐색 알고리즘 ]
😈 탐색 목표: 찾고 있는 데이터, 특정한 값 or 탐색이 성공했는지 알려주는 판단 기준
😈 탐색 공간: 탐색 목표일 가능성이 있는 것을 모두 모아 놓은 집합
(cf. 값을 모아 놓은 목록이나 그래프 상의 모든 노드)
*상태(state): 탐색 공간에 있는 하나의 가능성
😈 탐색 알고리즘: 탐색을 진행하면서 따라야 하는 특정 절차나 지침을 모아 놓은 집합
👀완전 탐색(exhaustive search)알고리즘👀
목푯값을 찾을 때 까지 탐색 공간 내 모든 가능성을 탐색하는 알고리즘(=노가다💢)
가능성을 순서대로 확인하는 선형 탐색을 가장 많이 사용
*선형 탐색 알고리즘:
장점💗-실제 구현이 간단하고 데이터가 구조화되어 있지 않아도 이 알고리즘을 사용할 수 있음.💩👌
단점💔-데이터가 구조화되어 있고 이 구조를 탐색에 활용할 수 있는 경우에는 완전 탐색 알고리즘보다 다른 알고리즘을 사용하는 편이 효율적임.⏱💢
효율적인 알고리즘👉 정보🤍
📂배열(array)📂
값을 여러 개 저장할 수 있는 간단한 자료구조
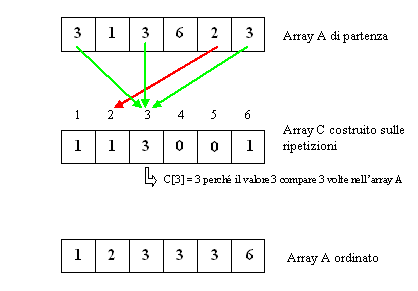
Array
배열의 각 칸에는 숫자나 문자 같은 정보를 하나씩 저장 (=☝칸 ☝정보)
장점💗-인덱스🔖 지정
배열 안에 있는 각 값에 쉽게 접근 👉 배열 요소 저장, 가져오기🥰👍 ➕ 탐색 간소화⏱
많은 프로그램 언어에서 0-인덱스 배열 사용
*0-인덱스 배열🔖: 0부터 시작, 첫 번째 값의 인덱스 0, 두 번째 값의 인덱스 1, 세 번째 인덱스 2···
*A[i]: 배열에 든 배열 요소를 나타내는 기호
배열을 뜻하는 Array의 A + 인덱스를 뜻하는 index의 i
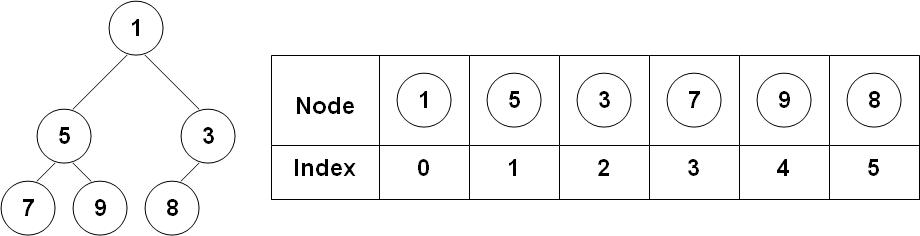
cf. 앞의 그림에서 A라는 배열의 세 번째 배열요소는 A[2]라고 나타내며 값은 3이 된다.
문자열🅰🅱
배열 = 숫자 + 문자열(텍스트 문자)을 저장할 때 사용
많은 프로그램 언어가 문자열을 배열로 처리
❗ 배열의 각 칸에는 글자, 숫자, 특수기호, 공백을 포함한 단 한 개☝의 문자만 ❗
다른 배열과 마찬가지로 문자열 속 문자도 인덱스를 사용해 바로 접근 가능💗
다음 포스팅💌👉 👍👎이진 탐색(binary search) + 🔧변형