[백준/3020] 개똥벌래 (Java)

Question

• 문제 링크 : https://www.acmicpc.net/problem/3020

• 분류 : 이진탐색

• 풀이 시간 : 90분

  이분탐색은 진짜 쥐약인 분야...

  많이 풀어서 접근하는 방법/시야를 키워야겠다

문제 해설

1. 높이가 M, 길이가 N인 동굴에 위쪽에는 종유석이 달려있고, 밑에는 석순이 있음
2. 종유석과 석순은 각각의 높이를 가지고 있고, 무조건 석순이 맨 먼저 시작함
3. 개똥벌래는 구간을 직진해서 동굴을 지나감
4. 개똥벌래는 장애물을 피하지 않아서, 지나가다가 종유석이나 석순을 만나면 부숨
5. 구간마다 부숴야하는 개수가 다름
6. 개똥벌래가 파괴해야하는 종유석+석순의 개수의 최솟값과 그런 구간이 몇개 있는지 구하시오

Solution

풀이 접근 방법

1. 각 높이마다 종유석과 석순을 몇 개 통과할 수 있는지 구함

   1. 전체 개수 - 통과 개수 = 부수는 개수
   2. 각각 부수는 개수 를 더해서 최소가 될 때를 고르자

2. (밑에서 시작하는 높이 기준) 높이가 n일 때

   1. 아래에서부터 시작하는 석순은 n 높이를 지나간다 가정
   2. 위에 달려있는 종유석은 H(전체 높이) - n + 1 높이를 지나간다 가정

3. 높이를 기준으로 해당 높이일 때 , 몇개를 부수지 않고 통과 가능한지 이분탐색

   

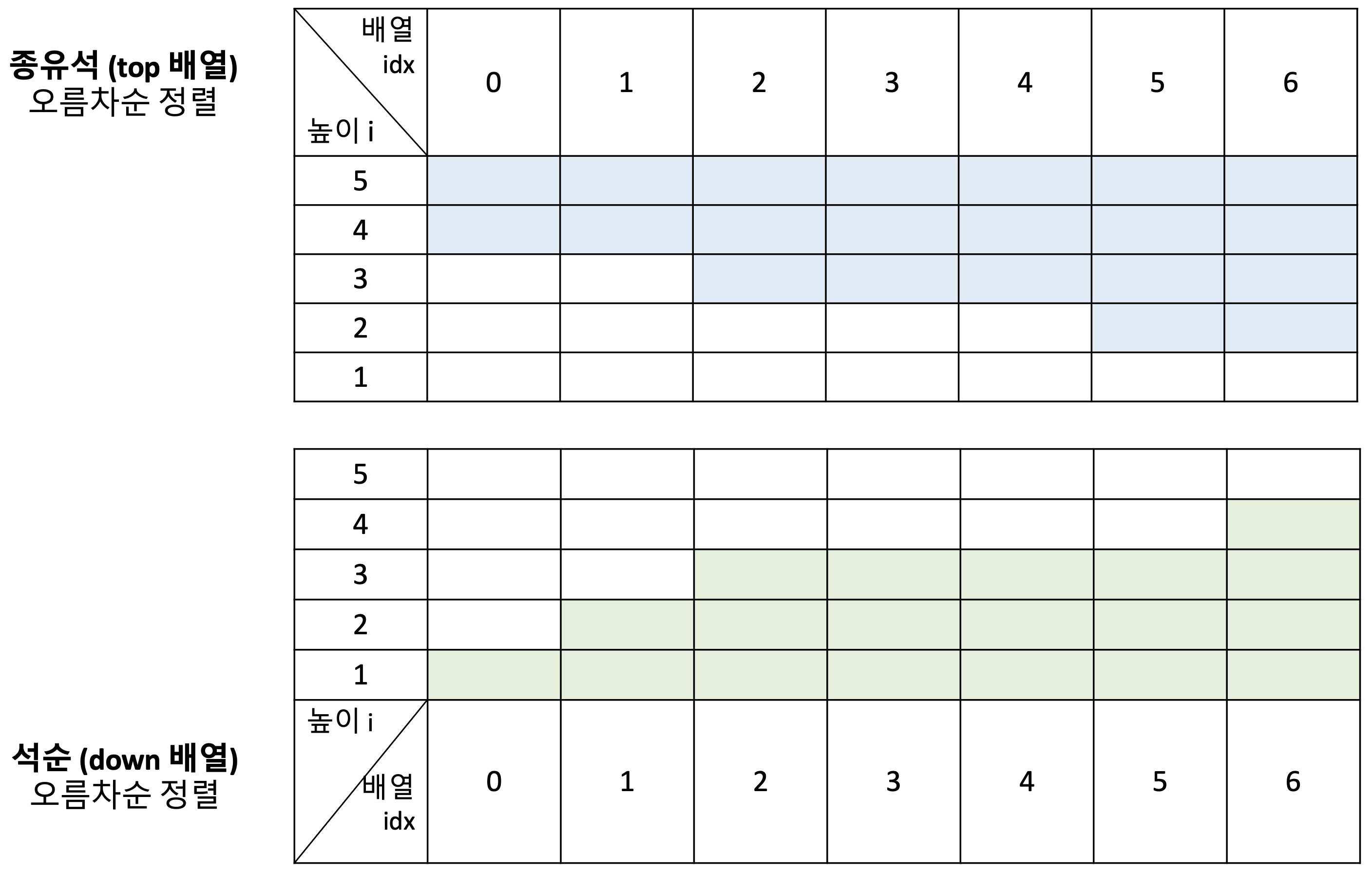
   개똥벌래 이동 높이	석순 높이	통과 여부
   3	2	부수지 않고 통과 가능
   3	3	부숴야 통과 가능
   3	4	부숴야 통과 가능

4. 이분탐색 로직

   • 높이 <= 석순 배열[이분 탐색 mid]

     • mid 이후 값들은 다 부딪힘
     • => 범위 왼쪽으로 이동

   • 높이 > 석순 배열[이분 탐색 mid]

     • mid 이전 값들은 모두 통과 가능
     • => 더 가능한지 범위 오른쪽으로 이동

정답 코드

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.Arrays;
import java.util.StringTokenizer;

public class Main {
  static int N, H;

  public static void main(String[] args) throws IOException {
    BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
    StringTokenizer st = new StringTokenizer(br.readLine());

    N = Integer.valueOf(st.nextToken());
    H = Integer.valueOf(st.nextToken());
    // 종유석
    Integer[] top = new Integer[N / 2];
    // 석순
    Integer[] down = new Integer[N / 2];

    int tIdx = 0, dIdx = 0;

    for (int i = 0; i < N; i++) {
      if (i % 2 == 0) {
        down[dIdx++] = Integer.valueOf(br.readLine());
      } else {
        top[tIdx++] = Integer.valueOf(br.readLine());
      }

    }

    Arrays.sort(top);
    Arrays.sort(down);
    int totalObj = down.length;
    int minBreak = Integer.MAX_VALUE;
    int count = 0;

    for (int i = 1; i <= H; i++) {
      // 지나가는 구간이 i 높이일 때
      // 전체 석순 개수 - 통과할 수 있는 개수
      int downBreak = totalObj - passCntByBS(i, down);
      // 전체 종유석 개수 - 통과할 수 있는 개수
      int topBreak = totalObj - passCntByBS(H - i + 1, top);
      int totalBreak = downBreak + topBreak;

      if (totalBreak < minBreak) {
        minBreak = totalBreak;
        count = 1;
      } else if (totalBreak == minBreak) {
        count++;
      }
    }

    bw.write(minBreak + " " + count + " \n");
    bw.flush();
    bw.close();

  }

  static int passCntByBS(int height, Integer[] arr) {
    int start = 0;
    int end = arr.length - 1;
    int maxPass = 0;

    while (start <= end) {
      int mid = (start + end) / 2;

      if (height <= arr[mid]) {
        end = mid - 1;
      } else {
        // 구하는건 몇개를 pass하는지
        // mid는 인덱스 값
        // 만약 0번 idx가 통과 가능한거면 1개가 지나칠 수 있는 것
        maxPass = Math.max(maxPass, mid + 1);
        start = mid + 1;
      }
    }

    return maxPass;
  }

}