BOJ - 1459 걷기

leehyunjon·2022년 6월 13일

boj 분기 수학

Algorithm

목록 보기

63/162

1459 걷기 : https://www.acmicpc.net/problem/1459

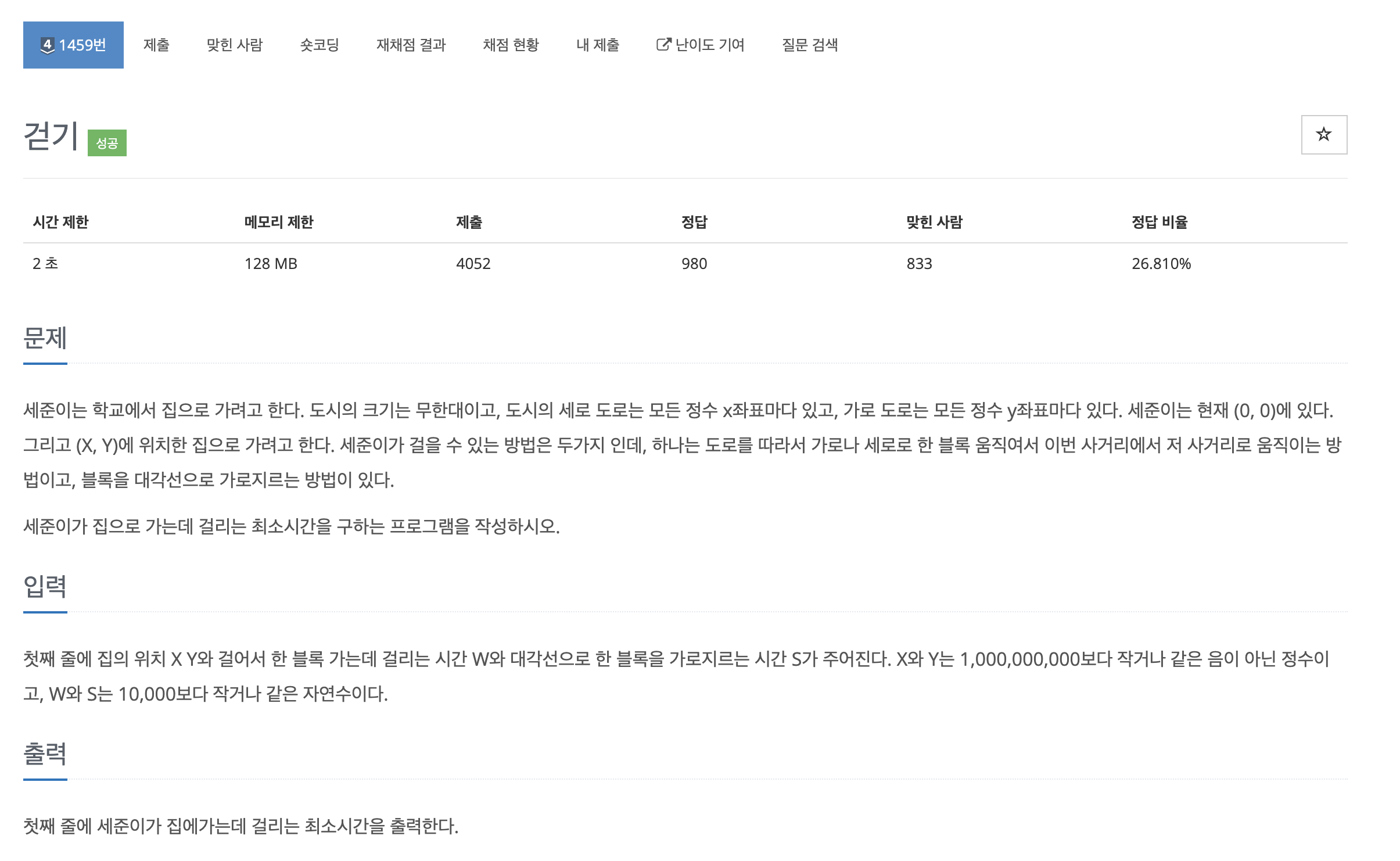
Problem

Solve

좌표의 최대값이 (10억, 10억)이기 때문에 모든 경우의 수를 하나하나 찾을수 없다.
이동할수 있는 경우의 수를 직접 찾아서 처리해야했다.

걸을 수 있는 방법은 두가지 방법이 있다고했다.
가로나 세로로 한칸씩 이동하는것과 대각선으로 가로지르는 방법이 있다.

평면으로 이동하는 경우 (X+Y)*W

대각선으로 이동하는 경우

X+Y가 양수일때 Math.max(X,Y)*S
X+Y가 음수일때 (Math.max(X,y)-1)*S+W

이 두 값 중 최소값을 최소거리로 생각했다.

하지만 반례가 있었다.

X = 4, Y = 1이고 W = 2, S = 3 인 경우

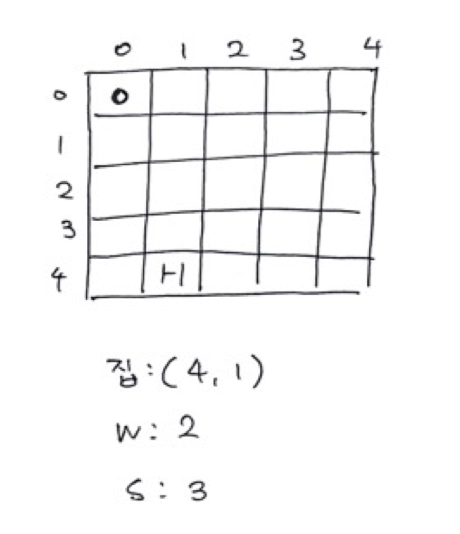
평면 이동시 5*2 = 10

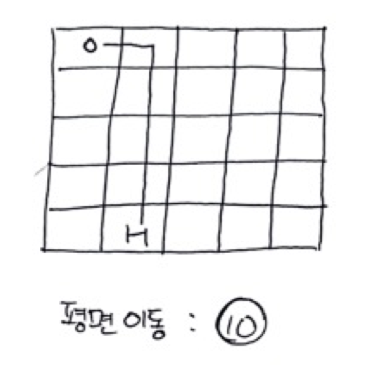
대각선 이동시 (3*3)+2 = 11 가 되어 평면이동이 최소거리로 나오게된다.

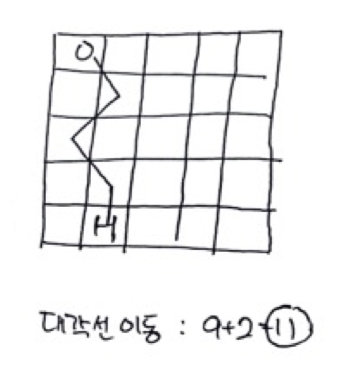
하지만 대각선과 평면 이동을 함께 이동시킨다면 대각선이동(13)+평면이동(32) = 9 가 되어 최소거리가 나오게 된다.
이는 대각선 이동시 대각선으로 이동(S) < 평면 이동(2W)이고 평면이동시 대각선으로 이동(2S) > 평면으로 이동(2W)가 될때 대각선으로 이동할수 있는 최소 이동거리만큼 이동 + 평면으로 최소 이동거리만큼 이동을 하게 하는 경우이다.

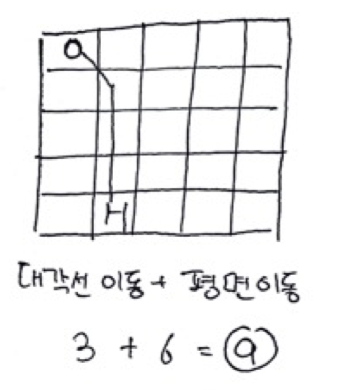
그리고 이동하는 좌표의 최대값이 각각 10억이므로 long 타입을 사용해줘야한다.

Code

public class 걷기 {
	public static void main(String[] args) throws IOException {
			BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
			BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

			StringTokenizer st = new StringTokenizer(br.readLine(), " ");
			int x = Integer.parseInt(st.nextToken());
			int y = Integer.parseInt(st.nextToken());
			int w = Integer.parseInt(st.nextToken());
			int s = Integer.parseInt(st.nextToken());

			//평면 이동
			long move1 = (long) (x+y)*w;

			//대각선 이동
			long move2 = 0;
			if((x+y)%2 == 0) move2 = (long) Math.max(x,y)*s;
			else move2 = (((long)Math.max(x,y)-1)*s)+w;

			//대각선 + 평면
			long move3 = 0;
			long cross = (long)Math.min(x,y)*s;
			long straight = ((long)Math.max(x,y)-(long)Math.min(x,y))*w;
			move3 = cross+straight;

			long answer = Math.min(move1, Math.min(move2,move3));

			bw.write(String.valueOf(answer));
			bw.flush();
			bw.close();
	}
}