BOJ - 1644 소수의 연속합

Problem

---

Solve

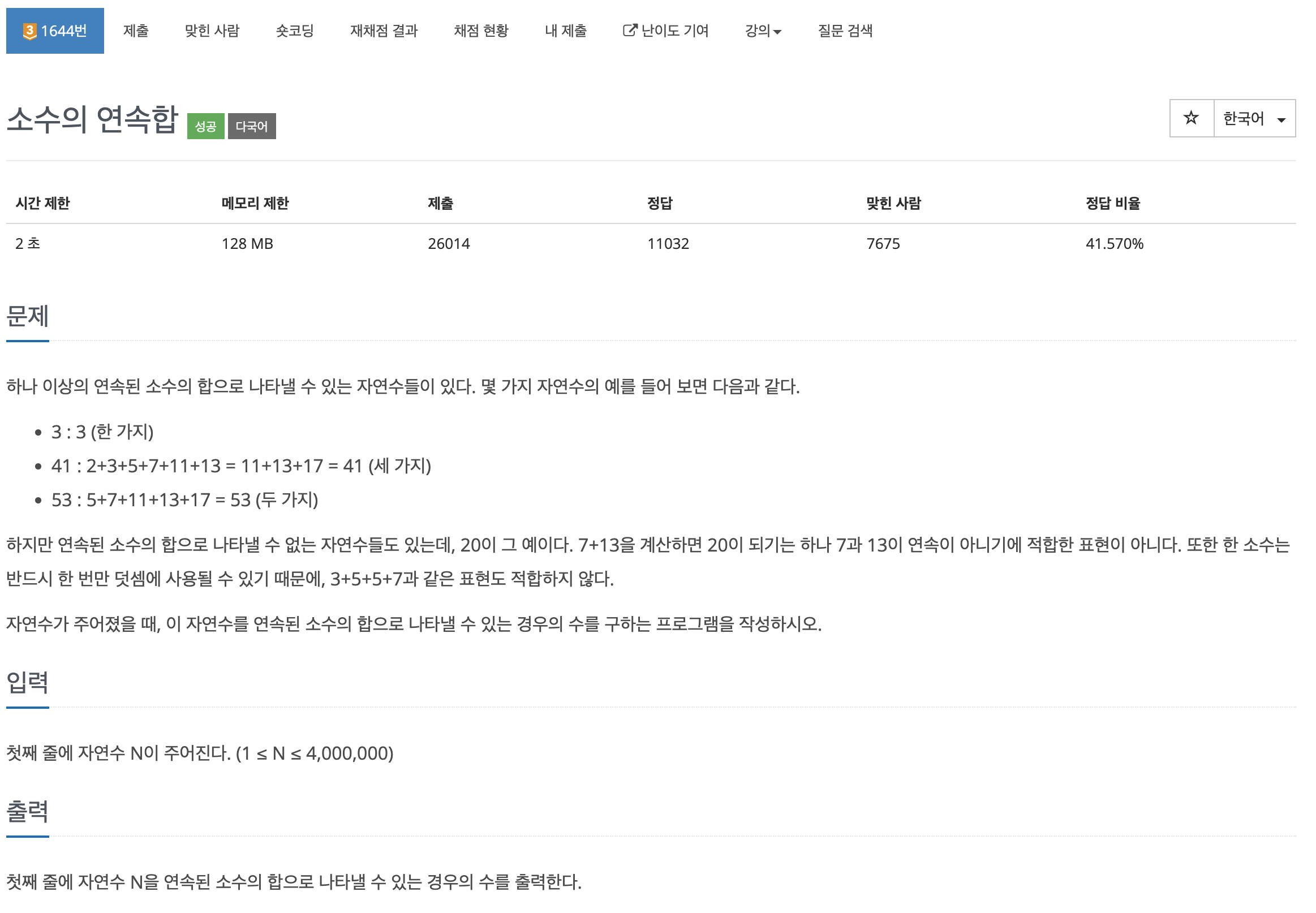
연속된 소수의 합이 주어진 N이 되는 개수를 구하는 문제.

이 문제는 N까지의 소수를 구한다음 연속되는 소수의 합이 N이 되는 것을 투 포인터를 이용해 해결한다.

구현 방법은 쉽게 떠올랐지만 투포인터에서 조건을 맞추는데 조금 까다로웠던것 같다.

먼저 N까지의 소수 리스트를 에라토스테네스의 체를 통해 초기화한다.

static List<Integer> setPrimes() {
		boolean[] isPrimes = new boolean[N + 1];
		List<Integer> primeList = new ArrayList<>();

		Arrays.fill(isPrimes, true);
        //0과 1은 소수가 아니다.
		isPrimes[0] = isPrimes[1] = false;

		//해당 값의 소수 여부는 2부터 N의 제곱근까지 비교한다.
		for (int i = 2; i <= Math.sqrt(N); i++) {
			if (isPrimes[i]) {
            //소수인 값의 제곱부터 N까지 해당 값의 배수는 소수가 아니다.
				for (int j = i * i; j <= N; j += i) {
					isPrimes[j] = false;
				}
			}
		}

		//소수인 값들을 list에 저장한다.
		for (int i = 0; i < isPrimes.length; i++) {
			if (isPrimes[i])
				primeList.add(i);
		}

		return primeList;
	}

에라토스테네스의 체로 소수를 구하는 것은 2부터 N제곱근까지의 값 중 소수인 값들의 제곱부터 N까지 소수가 아님으로 변경해주는 것으로 공식 이해만 하고 그냥 외워버렸다.

소수 리스트를 구했다면 start=0, end=0으로 초기화한 후 연속된 소수의 합을 투 포인터로 비교하면서 포인터를 이동시켜줘야한다.

	static int countPrime(List<Integer> primeList) {
		int start = 0;
		int end = 0;

		int count = 0;
		int sum = 0;

        //sum을 구한 후 end가 다음 위치로 이동하므로 end포인터가 sum의 범위보다 한칸 더 뒤에 있다.
        //그렇기 때문에 sum계산 후 sum==N을 비교한다.
        //그 후 sum>N인 경우 sum의 범위를 줄여주기 위해 start를 이동시켜준다.
        //sum==N인 경우 sum을 계산한 직후 sum==N을 비교해서 count를 갱신시켜주기 때문에 sum의 범위를 줄여서 sum<N일 때로 계산해주게 된다.
		while(true){
			if(sum>=N){
				sum -= primeList.get(start++);
			}
            
            else if(end == primeList.size()){
				break;
			}
            else{
				sum += primeList.get(end++);
			}

			if(sum == N) count++;
		}
		return count;
	}

---

Code

public class 소수의연속합 {
	static int N;

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

		N = Integer.parseInt(br.readLine());

		List<Integer> primeList = setPrimes();

		int answer = countPrime(primeList);

		bw.write(String.valueOf(answer));
		bw.flush();
		bw.close();
	}

	static int countPrime(List<Integer> primeList) {
		int start = 0;
		int end = 0;

		int count = 0;
		int sum = 0;

		while(true){
			if(sum>=N){
				sum -= primeList.get(start++);
			}else if(end == primeList.size()){
				break;
			}else{
				sum += primeList.get(end++);
			}

			if(sum == N) count++;
		}
		return count;
	}

	static List<Integer> setPrimes() {
		boolean[] isPrimes = new boolean[N + 1];
		List<Integer> primeList = new ArrayList<>();

		Arrays.fill(isPrimes, true);
		isPrimes[0] = isPrimes[1] = false;

		for (int i = 2; i <= Math.sqrt(N); i++) {
			if (isPrimes[i]) {
				for (int j = i * i; j <= N; j += i) {
					isPrimes[j] = false;
				}
			}
		}

		for (int i = 0; i < isPrimes.length; i++) {
			if (isPrimes[i])
				primeList.add(i);
		}

		return primeList;
	}
}

---

Result

아직 구현력이 많이 부족한것 같다.

---

Reference