1911 흙길 보수하기 : https://www.acmicpc.net/problem/1911
Problem
Solve
모든 웅덩이를 널판지로 덮기위한 최소 개수를 구하는 문제.
웅덩이의 최대 위치가 10억이므로 하나하나 웅덩이의 넓이를 구해 널판지를 덮기에는 시간초과가 발생한다.
웅덩이의 시작 위치를 오름차순으로 정렬 한 후, 웅덩이 시작 위치에서 끝 위치까지 널판지를 덮을 개수를 연산으로 구하는 방식을 사용했다.

설명을 이해하기 위해 배열 개념을 사용했다.
배열의 Index를 웅덩이의 가장자리라고 생각하자.
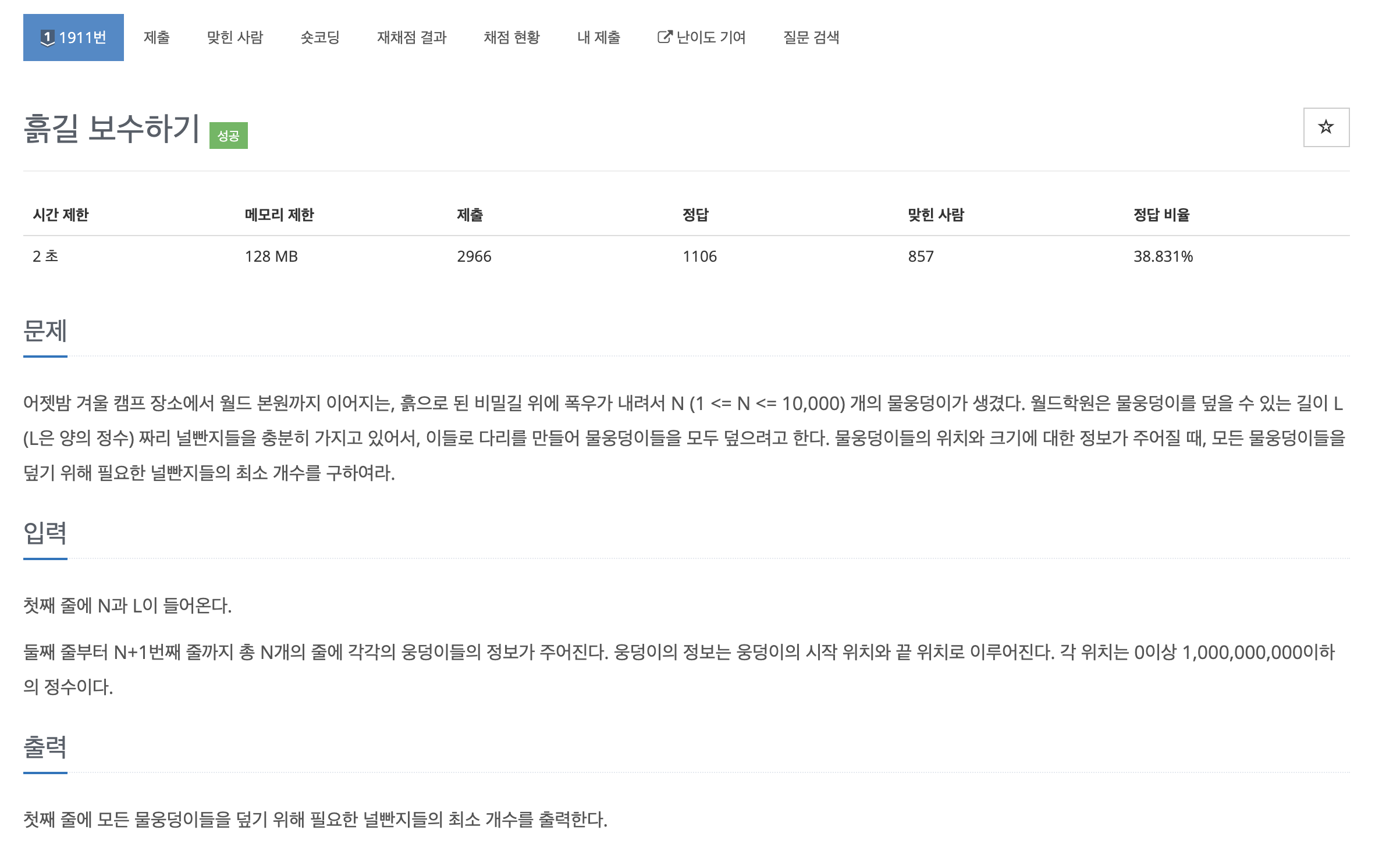
웅덩이의 시작 위치가 1, 끝 위치가 6일 때 웅덩이의 범위는 index 2부터 6까지다.
웅덩이의 시작 위치가 8, 끝 위치가 12일 때 웅덩이의 범위는 index 9부터 12까지다.
웅덩이의 시작 위치가 13, 끝 위치가 17일 때 웅덩이의 범위는 index 14부터 17까지다.
이를 기반으로 웅덩이를 덮은 후 널판지의 마지막 위치를 기억하며 다음 웅덩이를 덮기 위한 널판지를 몇개 더 덮어야 하는지 연산한다.
예를 들어 board를 널판지의 마지막 위치라고 하자.
널판지 길이는 3, board를 0으로 초기화한다.
첫번째 웅덩이의 시작 위치 start가 1, 끝 위치 end가 6일 때
board < start이므로 board = start = 1
웅덩이의 범위는 end-start = 5이므로 웅덩이를 덮기 위해 널판지는 총 2개가 필요하다.
board += 2(필요한 널판지 개수) * 3(널판지 길이)
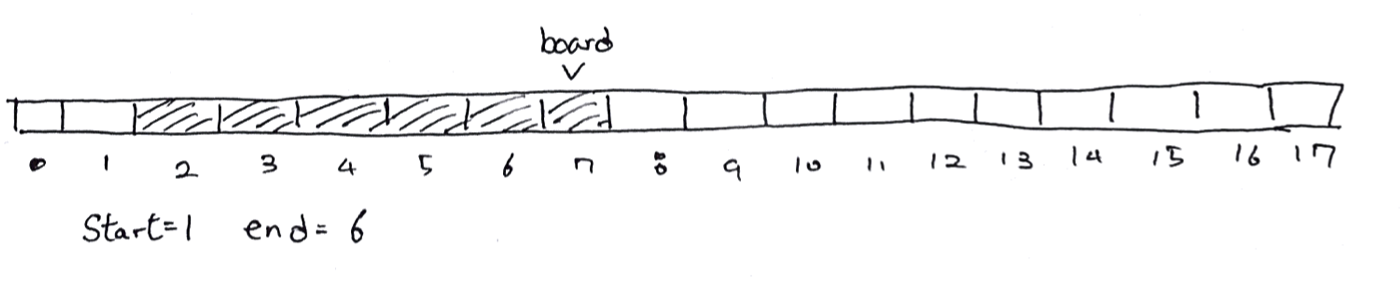
첫번째 웅덩이를 덮기 위해 총 2개의 널판지가 필요했고 널판지를 덮은 후 널판지의 마지막 위치는 7위치에 있다.
두번째 웅덩이의 시작 위치 start가 8, 끝 위치 end가 12일 때
board < start이므로 board = start = 8
웅덩이의 범위는 end-start = 4이므로 웅덩이를 덮기 위해 널판지는 총 2개가 필요하다.
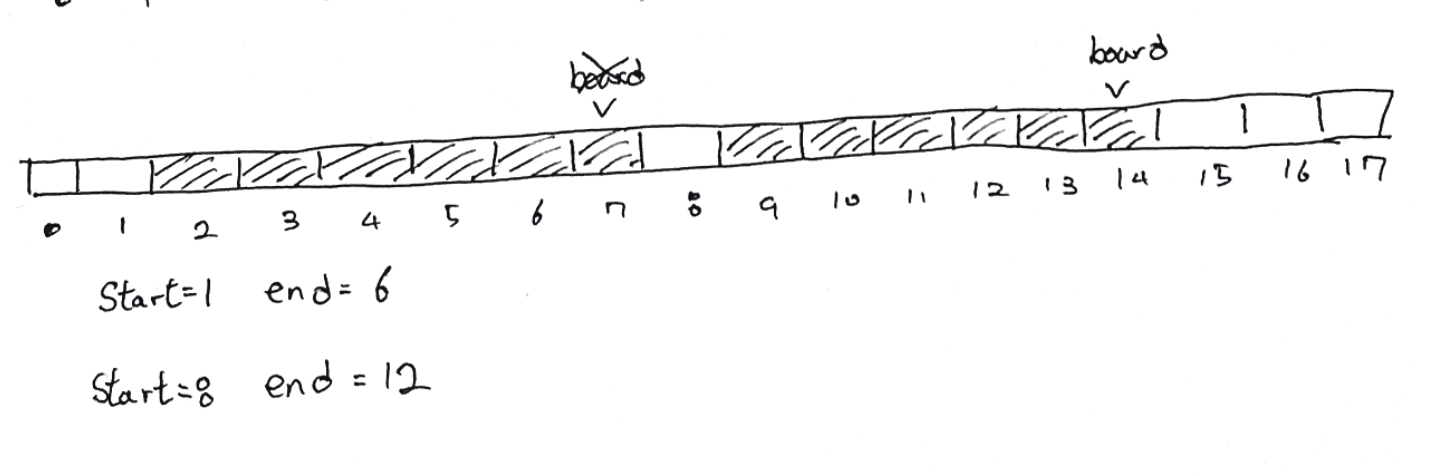
두번째 웅덩이를 덮기 위해 총 2개의 널판지가 필요했고 널판지를 덮은 후 널판지의 마지막 위치는 14위치에 있다.
세번째 웅덩이의 시작 위치 start가 13, 끝 위치 end가 17일 때
board >= start이므로 board = board = 14
웅덩이의 범위는 end-start = 4이지만 널판지는 이미 start를 넘어 14위치까지 덮고 있기 때문에 end까지 덮기 위해서는 end-board = 3의 범위만 덮어주면 되므로 총 1개의 널판지가 필요하다.
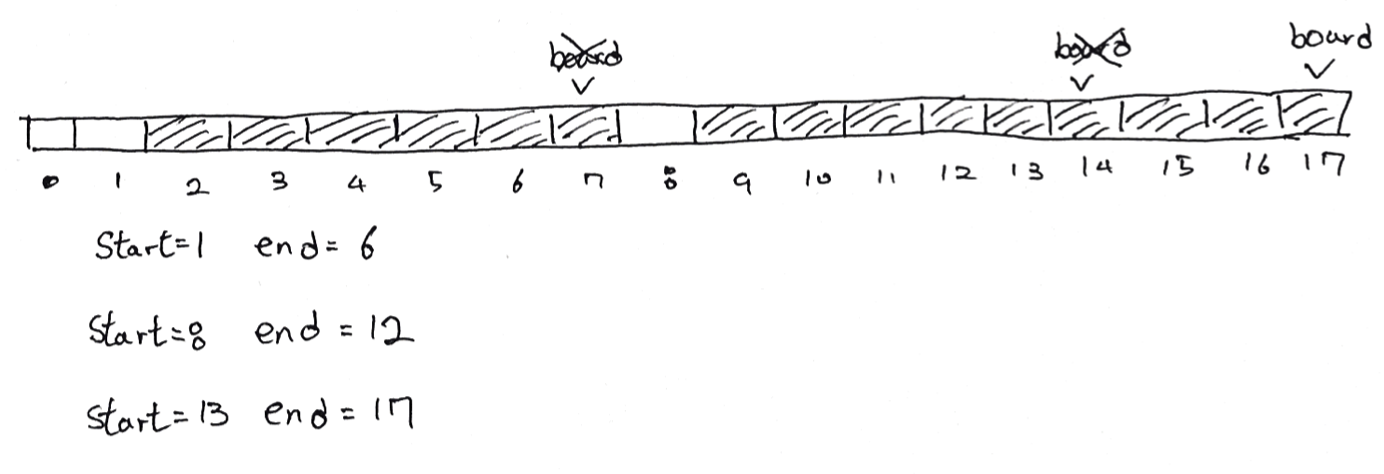
결국 모든 웅덩이를 덮기 위한 널판지의 총 개수는 2+2+1 = 5개가 필요하게 된다.
Code
public class 흙길보수하기 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int N = Integer.parseInt(st.nextToken());
int L = Integer.parseInt(st.nextToken());
int[][] pools = new int[N][2];
for (int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine(), " ");
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
pools[i] = new int[] {start, end};
}
//웅덩이 시작 위치 오름차순 정렬
Arrays.sort(pools, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[0] - o2[0];
}
});
//널판지 총 개수
int boardCount = 0;
//널판지 마지막 위치
int board = 0;
for (int[] pool : pools) {
int start = pool[0];
int end = pool[1];
//널판지의 위치와 웅덩이 시작위치 중 더 큰 값 부터 널판지를 덮는다.
board = Math.max(board, start);
//웅덩이의 끝 위치가 현재 널판지의 위치보다 뒤에있거나 같다면 이미 덮혀있음
if(end <= board) continue;
//널판지가 덮어야하는 범위
int distance = end - board;
//필요한 널판지 개수 올림.
int count = (int) Math.ceil((double)distance/L);
//널판지 위치 갱신
board += (L*count);
//널판지 개수 추가
boardCount += count;
}
bw.write(String.valueOf(boardCount));
bw.flush();
bw.close();
}
}
