BOJ - 3151 합이 0

leehyunjon·2022년 5월 25일

boj 투포인터

Algorithm

목록 보기

41/162

3151 합이 0 : https://www.acmicpc.net/problem/3151

Problem

Solve

총 3개의 경우의 수를 찾아야하므로 3중 반복을 쓰게 되면 O(10000^3)으로 시간초과가 발생하게된다.
기준 한명만 반복문을 쓰고 나머지 두명은 투 포인터를 이용한다면 O(10000*10000)으로 해결할수 있다.

3개의 경우의 수를 찾는 것이기 때문에 순서는 필요없으므로 정렬 후 기준이 되는 값과 나머지 두 값의 합이 0에 가까운 수가 아닌 0이 되는 것을 찾는 것이기 때문에 세 값의 합이 0일 때와 0이 아닌 경우를 나누어 생각해볼수 있다.

0인 경우 그냥 나머지 두 값을 가리키는 포인터(start, end)를 이동시키면 되지않을까? 라는 생각을 했었다. 하지만 start+1의 값이나 end-1의 값 중 하나를 움직였을 때 같은 결과값을 가지는 경우를 놓칠수도 있다는 것을 놓쳤다.
예를 들어 [-5,2,2,2,3,3]으로 정렬된 배열이 있다고 할때 기준 값이 -5이고, start=1, end=5라고 하자. -5 + arr[start] + arr[end] = 0 이기 때문에 조건으로 start+1로 앞의 값들로 경우의 수를 만들자니 end-1의 경우를 놓치게 되고((2,3),(2,3),(2,3),(3,3)의 경우가 된다) end-1로 하자니 ((2,3),(2,3),(2,2),(2,2)의 경우가 된다.)
그렇기 때문에 0이 나온 경우 arr[start]와 같은 값의 개수와 arr[end]와 같은 값의 갯수를 구해서 경우의 수를 만들어 주는 것이다.

만약 arr[start] == arr[end]라면 배열은 정렬되어있는 상태이기 때문에 [end-start+1]C2의 경우의 수를 가지게 된다.

문제의 예시로 살펴보자

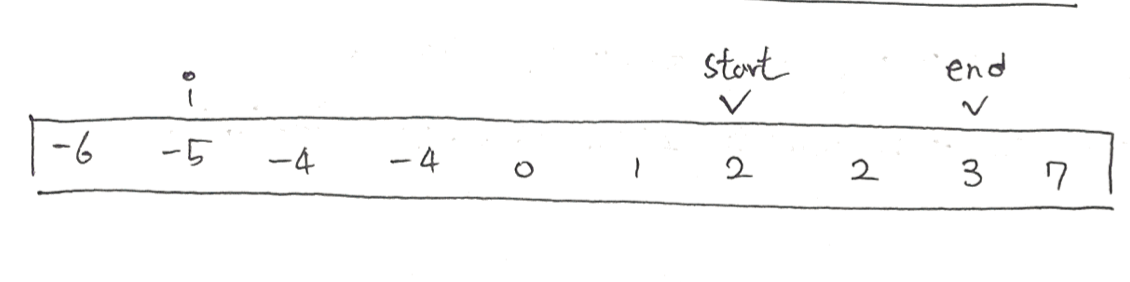
주어진 점수를 정렬하고 기준이 될 값을 arr[i], 나머지 두 값을 arr[start], arr[end]로 보았을 때, 기준 값 -5와의 합이 0이 되는 값은 start=6, end=8인 경우이다.
위에서 설명한대로 arr[start]와 같은 값의 개수와 arr[end]와 같은 값의 개수를 구하면

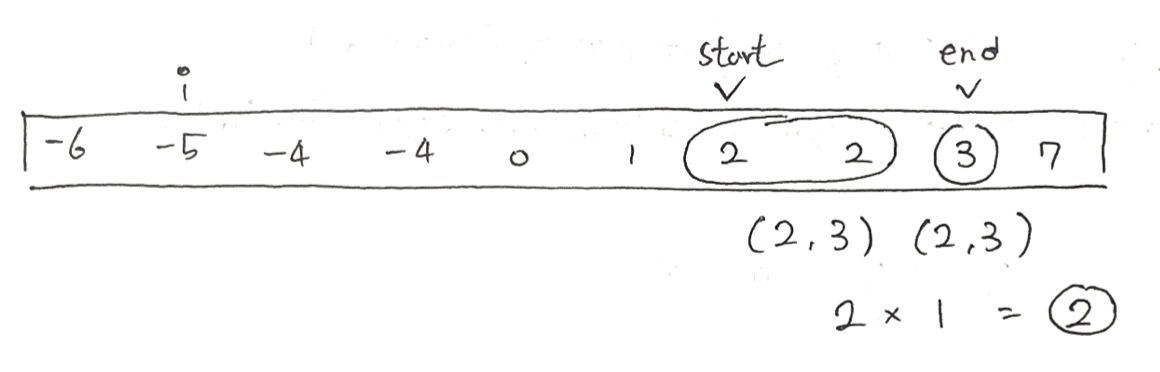
각각 2개와 1개가 나오고 이 둘을 곱하게 되면 arr[start]값 2와 arr[end]값 3으로 만들수 있는 경우의 수 2개를 도출할수 있게 된다.

arr[start] == arr[end] 인 경우 컴비네이션 계산을 통해 경우의 수를 도출할수 있다.

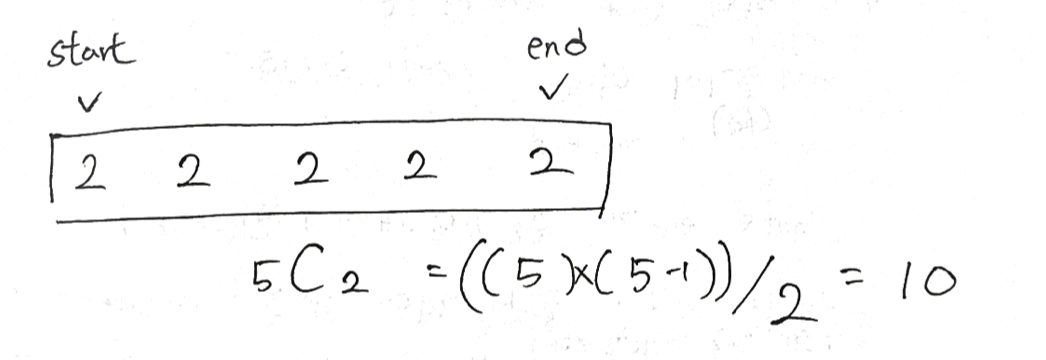
Code

public class 합이0 {
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
		int N = Integer.parseInt(br.readLine());
		int[] alp = new int[N];

		StringTokenizer st = new StringTokenizer(br.readLine()," ");
		for(int i=0;i<N;i++){
			alp[i] = Integer.parseInt(st.nextToken());
		}
        //오름차순 정렬
		Arrays.sort(alp);

		int answer=0;
        //기준 값 i
		for(int i=0;i<N-2;i++){
			int start=i+1;
			int end=N-1;
			while(start<end){
				int sum = alp[start]+alp[end];
				int target = -alp[i];
                //sum==target일 때 합이 0
				if(sum == target){
                	//합이 같은데 두개 포인터의 값이 동일할 경우 컴비네이션 계산으로 경우의수 도출 후 answer에 추가
					if(alp[start]==alp[end]){
						answer += combination(end-start+1);
						break;
					}else{
                    	//합이 같은데 두개 포인터의 값이 다른 경우
						int startCount=0;
						int endCount=0;
						int startIdx = start;
						int endIdx = end;
                        //alp[start]의 같은 값의 개수를 구한다.
						while(alp[startIdx]==alp[start]){
							startCount++;
							start++;
						}
                        //alp[end]의 같은 값의 개수를 구한다.
						while(alp[endIdx]==alp[end]){
							endCount++;
							end--;
						}
                        //alp[start]와 alp[end]의 경우의수 answer에 추가
						answer += startCount*endCount;
					}
				}else{
                //합이 같지 않은 경우
                	//다른 두개의 합이 더 큰 경우 두 개의 수 중 더 큰 값인 end를 줄인다.
					if(sum>target) end--;
                    //다른 두개의 합이 더 작은 경우 두 개의 수 중 더 작은 값인 start를 증가시킨다.
					else start++;
				}
			}
		}

		bw.write(String.valueOf(answer));
		bw.flush();
		bw.close();
	}

	static int combination(int n){
		return n*(n-1)/2;
	}
}