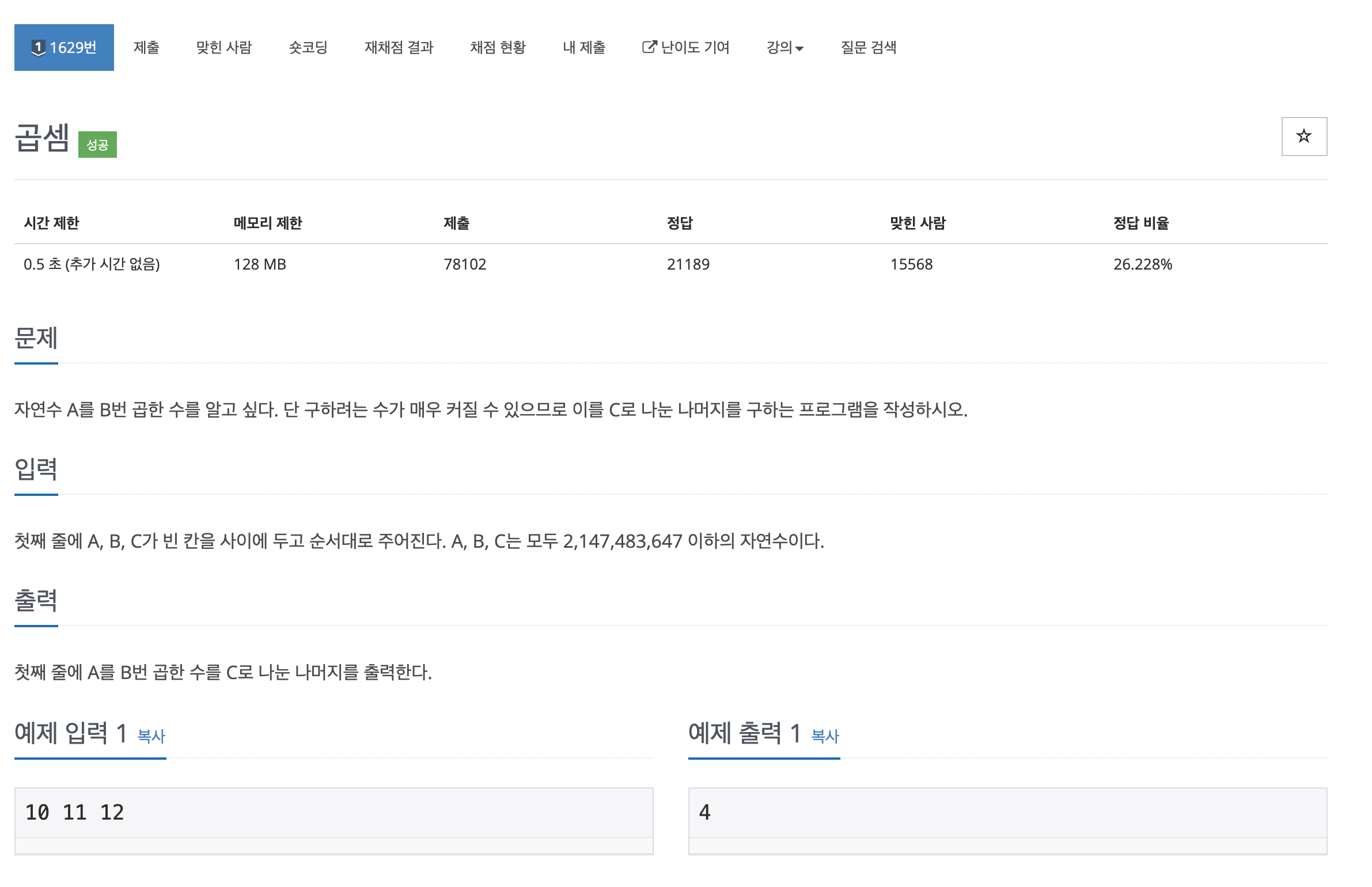
1629 곱셈 : https://www.acmicpc.net/problem/1629
Problem
Solve
단순하게 생각했을때 A를 B번 곱해서 C로 나눈 나머지를 구한다. 라고 생각할 수 있지만 B는 최대 21억이 넘는 값을 가지기 때문에 이러한 방법은 시간 초과가 발생합니다.
다른 접근법을 생각해봐야합니다.
바로 지수법칙과 모듈러법칙을 이용하여 N이 아닌 logN으로 A의 곱을 구할 수 있습니다.
지수법칙
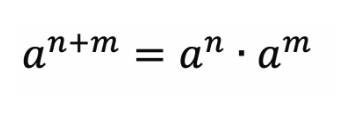
지수법칙을 이용하면 A^10이 있을때 A^5 * A^5로 나타낼수 있습니다.
지수가 홀수라면 A^11일때 A^5 * A^5 * A로 나타낼수 있습니다.
그렇다면 A가 10이고 B가 11일때 지수법칙을 이용하면 어떻게 될까요?
10^11은 10^5 * 10^5 * 10으로 나타낼 수 있습니다.
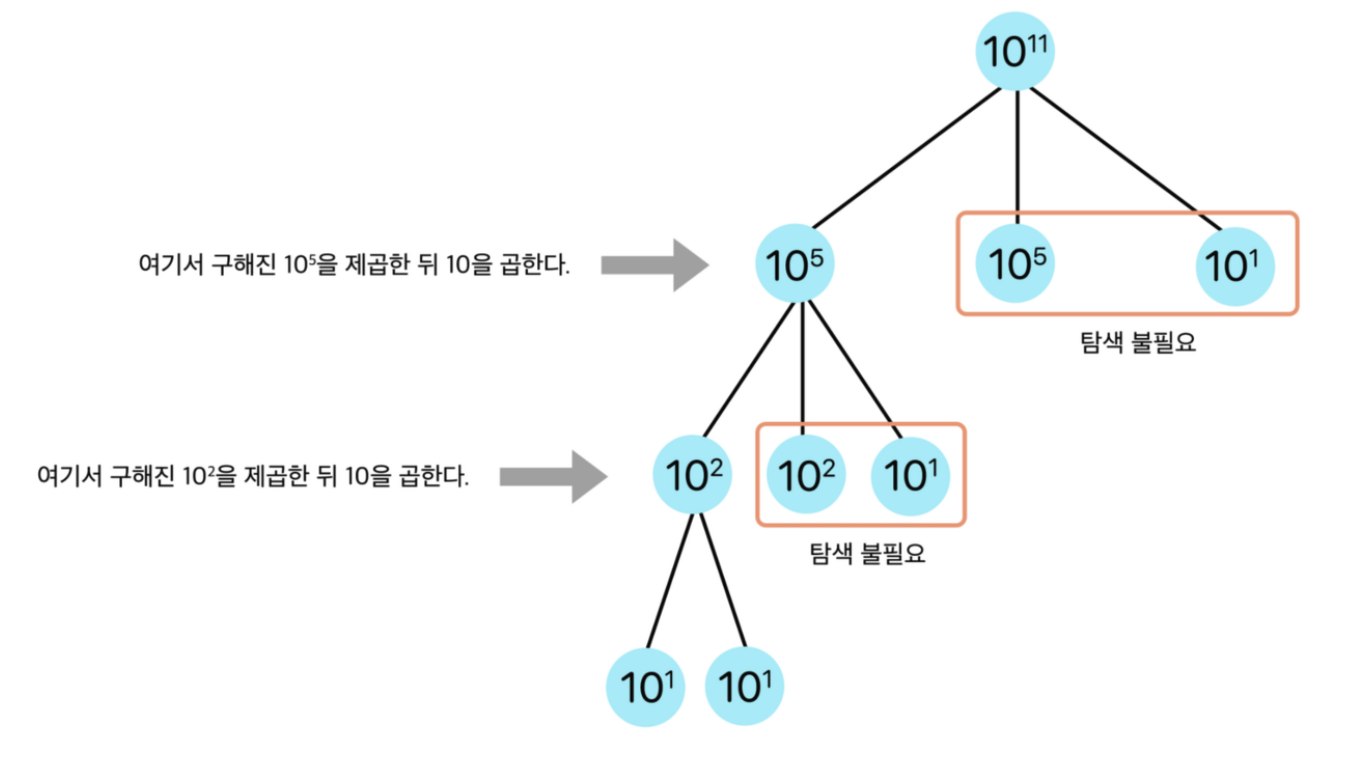
지수 법칙을 이용하면 위와 같은 형식으로 불필요한 계산을 하지 않고 logN의 시간복잡도로 곱을 계산할 수 있게 됩니다.
모듈러법칙
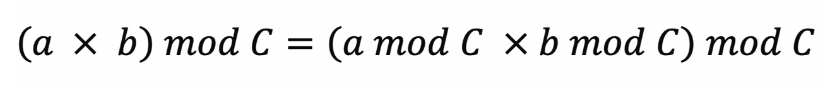
모듈러 법칙은 보시는바와 같이 A와 B 곱의 결과를 C로 나누어주었을때, 각각 C로 나누고 그 전체를 C로 나누는 것과 동일합니다.
지수법칙과 모듈러법칙을 이용해서 B를 절반으로 갱신해가며 A^B를 구해야하기 때문에 재귀를 이용합니다.
static long moduler(long A, long B, long C){
//지수값이 1이 된다면 더이상 곱할 값이 없습니다.
if(B==1) return A%C;
//지수법칙을 위한 A(재귀)
long tmp = moduler(A, B/2, C);
//지수가 짝수일떄와 홀수일때를 분기하여 A와 현재 B의 값으로 구할수 있는 곱을 반환합니다.
if(B%2==0) {
return (tmp*tmp)%C;
}else{
return (tmp*tmp)%C*A%C;
}
}Code
import java.io.*;
import java.util.StringTokenizer;
public class 곱셈{
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine()," ");
int A = Integer.parseInt(st.nextToken());
int B = Integer.parseInt(st.nextToken());
int C = Integer.parseInt(st.nextToken());
long answer = moduler(A,B,C);
bw.write(String.valueOf(answer));
bw.flush();
bw.close();
}
static long moduler(long A, long B, long C){
if(B==1) return A%C;
long tmp = moduler(A%C, B/2, C);
if(B%2==0) {
return (tmp*tmp)%C;
}else{
return (tmp*tmp)%C*A%C;
}
}
}Result
재귀 어렵다.
