BOJ - 네트워크 연결

leehyunjon·2022년 11월 11일

boj 최소 스패닝 트리

Algorithm

목록 보기

127/162

1922 네트워크 연결 : https://www.acmicpc.net/problem/1922

Problem

Solve

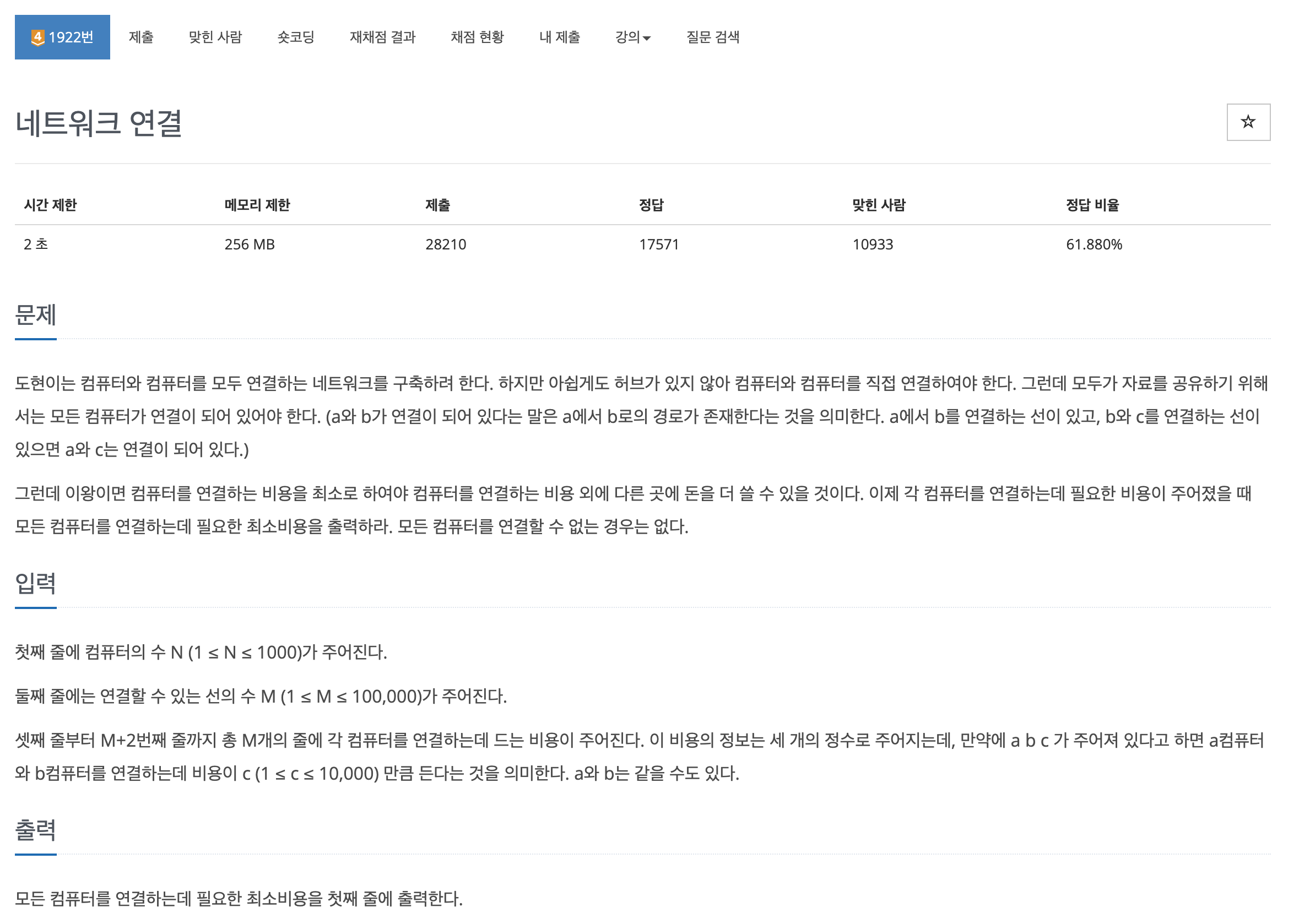
모든 정점을 연결할수 있는 최소의 가중치를 구하는 문제입니다.

최소 스패닝 트리를 이용하여 문제를 해결할수 있습니다.
또한 최소 스패닝 트리는 union find를 이용한 크루스칼 알고리즘방법과 priority queue를 이용한 프림 알고리즘을 사용한 방법이 있습니다.

공부할겸 둘 다 풀어보았습니다.

크루스칼 알고리즘

먼저 union find를 이용한 크루스칼 알고리즘 풀이입니다.

크루스칼은 주어진 간선의 정보 (시작점, 도착점, 가중치)를 저장합니다.
가중치를 기준으로 오름차순 정렬하고 시작점을 기준으로 오름차순 정렬을 수행하여줍니다.
저장된 간선 정보를 반복하면서 주어진 시작점과 도착점이 사이클이 발생 여부를 판단하고 사이클이 발생하지 않는 두 정점에 대해 가중치를 합해가며 반복합니다.
(union find를 이용하여 사이클 여부를 확인합니다)

크루스칼은 union find의 경우 상수의 시간복잡도를 가지고 간선을 반복하는 O(E)를 가집니다. 그렇기 때문에 간선을 정렬하는 시간복잡도 O(ElogE)가 크루스칼의 시간복잡도가 됩니다.

프림 알고리즘

Priority Queue를 이용한 프림 알고리즘 풀이입니다.

간선 정보를 이용하여 인접 리스트를 생성합니다.
가중치를 기준으로 오름차순 정렬이 정의되고 인접 정점과 가중치를 저장하는 PriorityQueue를 정의합니다.
PriorityQueue에 시작정점을 저장하고 PQ에서 가중치가 가장 적은 정점을 꺼내어 인접한 정점을 PQ에 저장하여 PQ가 빌때까지 반복합니다.
(이때, PQ에서 꺼내온 정점이 이미 방문되었던 정점이라면 해당 정점이 도달할수 있는 최소값으로 이미 도달한것이기 때문에 해당 정점은 더이상 방문하지 않습니다.)

프림은 모든 정점을 방문하면서 PQ의 정렬이 발생합니다. 이는 O(VlogV)가 됩니다.
그리고 인접 리스트를 통해 모든 정점을 방문하면서 PQ의 정렬로 인해 O(ElogV)가 됩니다.
보통 E가 V보다 크기때문에 O(ElogV)의 시간복잡도가 발생합니다.

Code

크루스칼

public class 네트워크연결_크루스칼{
	static int[] union;
	public static void main(String[] args) throws IOException{
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

		int N = Integer.parseInt(br.readLine());
		int M = Integer.parseInt(br.readLine());

		union = new int[N+1];
		List<Edge> edges = new ArrayList<>();
		for(int i=0;i<M;i++){
			StringTokenizer st = new StringTokenizer(br.readLine()," ");
			int a = Integer.parseInt(st.nextToken());
			int b = Integer.parseInt(st.nextToken());
			int c = Integer.parseInt(st.nextToken());

			edges.add(new Edge(a,b,c));
		}

		//union find 초기화
		for(int i=1;i<=N;i++){
			union[i]=i;
		}

		//간선 정보 오름차순 정렬
		Collections.sort(edges);

		int answer = 0;

		for(Edge e : edges){
        	//사이클이 발생하는 두 정점은 확인하지 않습니다.
			if(find(e.start) == find(e.end)) continue;

			answer += e.cost;
			union(e.start, e.end);
		}

		bw.write(String.valueOf(answer));
		bw.flush();
		bw.close();
	}

	static int find(int a){
		if(union[a]==a) return a;
		return union[a] = find(union[a]);
	}

	static void union(int a, int b){
		a = find(a);
		b = find(b);

		if(a>b){
			int tmp = b;
			b = a;
			a = tmp;
		}

		union[b] = a;
	}

	static class Edge implements Comparable<Edge>{
		int start;
		int end;
		int cost;
		public Edge(int start, int end, int cost){
			this.start = start;
			this.end = end;
			this.cost = cost;
		}

		@Override
		public int compareTo(Edge o){
			int result = this.cost - o.cost;
			if(result == 0) result = this.start - o.start;
			return result;
		}
	}
}

프림 알고리즘

public class 네트워크연결{
	public static void main(String[] args) throws IOException{
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

		int N = Integer.parseInt(br.readLine());
		int M = Integer.parseInt(br.readLine());
		List<int[]>[] graph = new List[N+1];
		int start = 1001;
		for(int i=1;i<=N;i++){
			graph[i] = new ArrayList<>();
		}

		for(int i=0;i<M;i++){
			StringTokenizer st = new StringTokenizer(br.readLine()," ");
			int a = Integer.parseInt(st.nextToken());
			int b = Integer.parseInt(st.nextToken());
			int c = Integer.parseInt(st.nextToken());
			if(a==b) continue;
			graph[a].add(new int[]{b,c});
			graph[b].add(new int[]{a,c});

			start = Math.min(start,Math.min(a,b));
		}

		int answer = MST(graph, start);

		bw.write(String.valueOf(answer));
		bw.flush();
		bw.close();
	}

	static int MST(List<int[]>[]graph, int start){
		PriorityQueue<int[]> pq = new PriorityQueue<>((o1, o2)->{
			return o1[1] - o2[1];
		});
		boolean[] check = new boolean[graph.length];

		pq.offer(new int[]{start,0});

		int totalCost = 0;

		while(!pq.isEmpty()){
			int[] current = pq.poll();
			if(check[current[0]]) continue;
			check[current[0]] = true;
			totalCost += current[1];

			for(int[] link : graph[current[0]]){
				if(check[link[0]]) continue;
				pq.offer(link);
			}
		}

		return totalCost;
	}
}