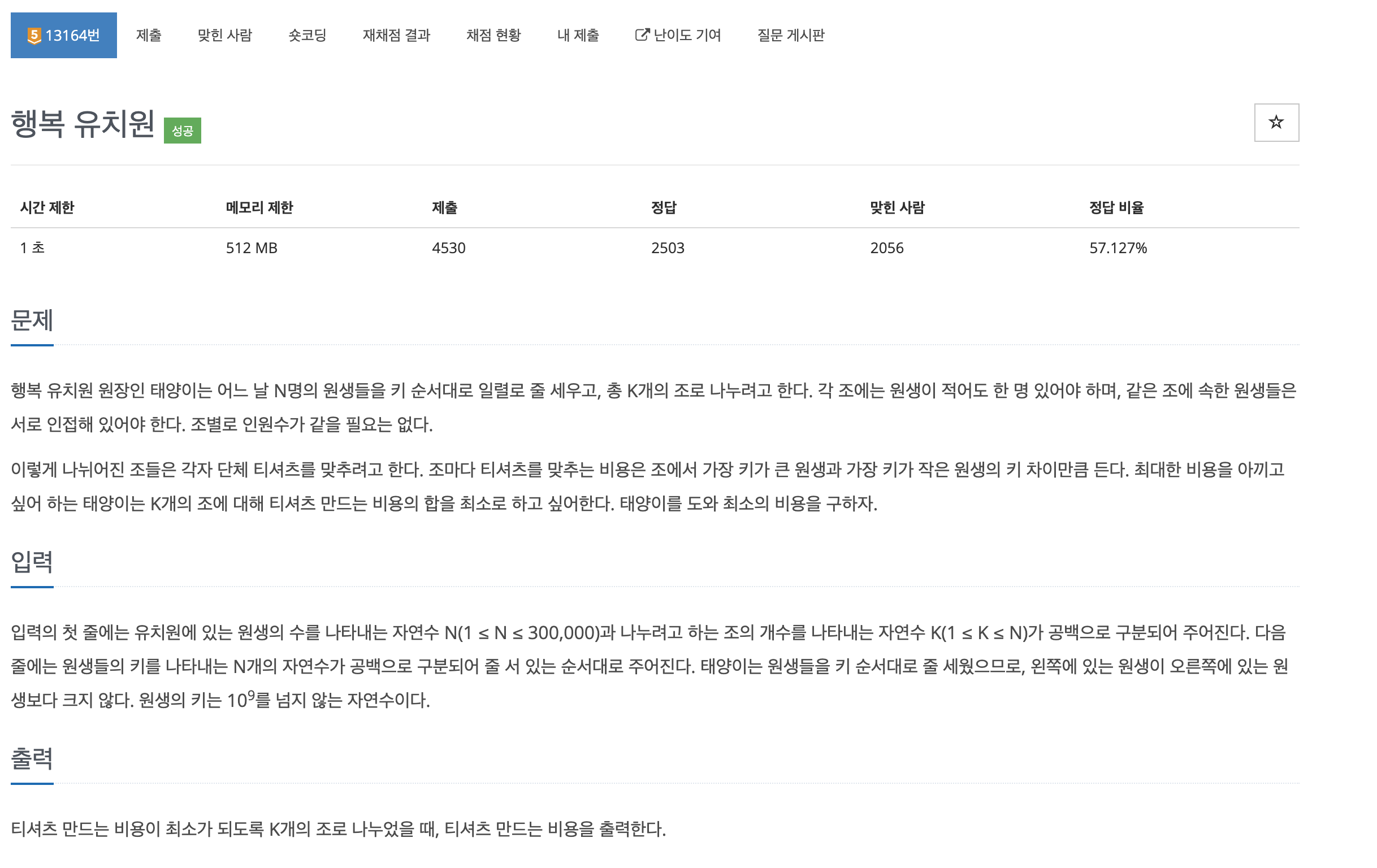
13164 행복 유치원 : https://www.acmicpc.net/problem/13164
Problem
Solve
처음 풀이는 이분탐색을 이용하여 최소가 되는 비용을 찾도록 그룹을 만들어주도록 구현하였습니다.
하지만 그룹에서 최소의 값을 찾아주는데 구현의 어려움이 있었고 다른 분의 풀이를 참고하였습니다.
해당 문제의 풀이 순서는 아래와 같습니다.
- X와 Y값의 차이는 X~Y사이의 각 요소들의 차이의 합을 구합니다.
- 각 요소들의 차이값을 오름차순 정렬하고 N-K까지의 합을 구합니다.
먼저 X와 Y사이의 각 요소들 차이의 합을 구하는 것입니다.
처음부터 이게 무슨 소리인가 싶었습니다. 각 요소들의 차이 합을 왜 구해야하는지를..
예를 들어 [1,4,5,6,7]의 수가 주어졌을때, 0번째의 1과 4번쨰의 7의 차이는 7-1 = 6입니다.
풀이하자면 4번째에 있는 값과 0번째에 있는 값의 차이는 그 값을 빼주면되고, 이는 (0번째,1번째), (1번째, 2번째), (2번째, 3번째), (3번째, 4번째)의 차이의 합이라는 것입니다.
(1,4), (4,5), (5,6), (6,7)의 값의 차는 각각 3, 1, 1, 1이되게 됩니다. 그리고 각 요소들의 차의 합은 3+1+1+1 = 6이되게 됩니다. 즉, 가장 큰값과 가장 작은값의 차이는 각 요소들 차의 합과 동일 하다는 것입니다.
식으로 표현하자면, X와 Y의 차이는 arr[Y]-arr[X] = arr[Y] + (-arr[Y-1] + arr[Y-1]) + (-arr[Y-2] + arr[Y-2]) + ... + (-arr[X+1] + arr[X+1]) - arr[X]이 되게 됩니다.
이는 각 요소들 차의 합은 배열의 가장 큰값과 가장 작은 값의 차가 된다는 뜻입니다.
//각 요소 students[]에서 각 요소들의 차를 저장하는 배열
int[] arr = new int[N-1];
for(int i=0;i<N-1;i++){
arr[i] = students[i+1]-students[i];
}그런 다음 요소들의 차를 저장한 배열을 오름차순 정렬합니다.
이 부분조차 이해하기 어려웠습니다. 어찌어찌 요소들의 차를 오름차순 정렬했다하더라도 이걸로 어떻게 그룹의 최소값을 구하는지를..
결과먼저 말하자면, N-K미만의 요소의 차이합을 구해야합니다.
왜 N-K이냐 하면
먼저 각 N개의 요소들이 그룹으로 이루어져있다면 N개의 그룹이 존재합니다.
1번 합치게 된다면 N-1개의 그룹이 생성되게됩니다.
2번 합치게 된다면 N-2개의 그룹이 생성되게 됩니다.
N-K번 합치게 된다면 K개의 그룹이 생성되게 됩니다.
예를 들어 1, 4, 5, 6, 7의 요소가 있고 N=5, K=3인 경우입니다.
현재 5개의 그룹이 존재합니다.
1번 합쳤을때 N-1개의 그룹이 됩니다.
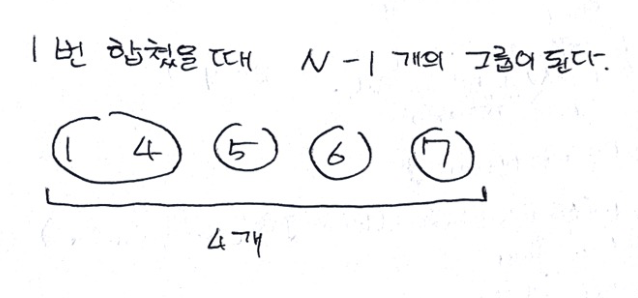
1과 4를 합친경우 (1,4), (5), (6), (7)의 그룹으로 총 4개의 그룹이 생성되게 됩니다.
2번 합쳤을때 N-2개의 그룹이 됩니다.
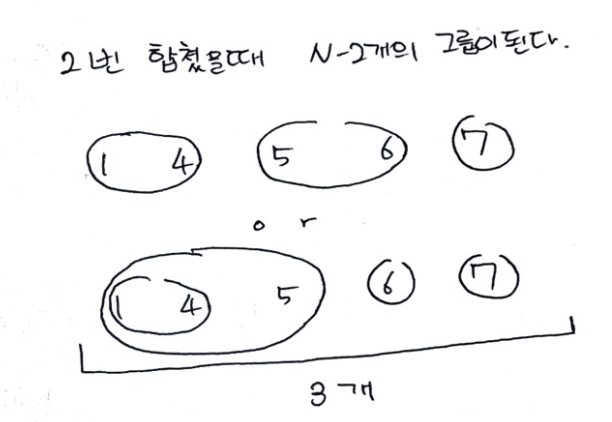
(1,4), (5,6), (7)의 그룹으로 묶거나 (1,4,5), (6), (7)의 그룹으로 묶거나 총 3개의 그룹이 생성되게 됩니다.
각 요소들의 차의 합과 K그룹을 만들기 위해 N-K를 합침을 이용하면 K개의 그룹을 이루는 최소값을 구할 수 있게 됩니다.
예를 들어 1, 4, 5, 6, 7의 요소가 있고 N=5, K=3인 경우를 들어보겠습니다.
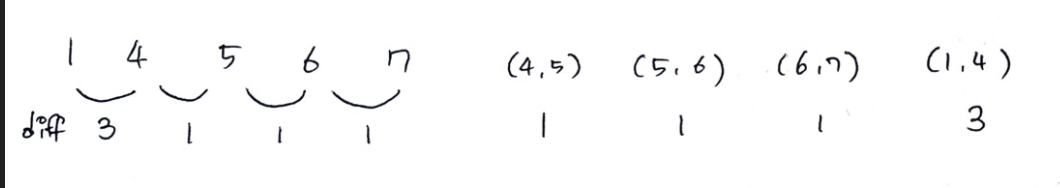
각 요소의 차를 구한다면 (1,4): 3 , (4,5): 1 , (5,6): 1 , (6,7): 1가 주어집니다.
그리고 이 각 차를 오름차순정렬한다면 [1,1,1,3]이 되게됩니다.
정렬된 값의 1들은 각각 (4,5), (5,6), (6,7)의 차이입니다.
그리고 그룹 4개를 생성하려는 경우 5(N)-4 = 1개의 차를 합하면 되므로 각 그룹의 합의 최소는 1이 되게됩니다.
그룹 3개를 생성하려는 경우 5(N)-3 = 2개의 차를 합하면 되므로 각 그룹의 합의 최소는 2가 되게됩니다.
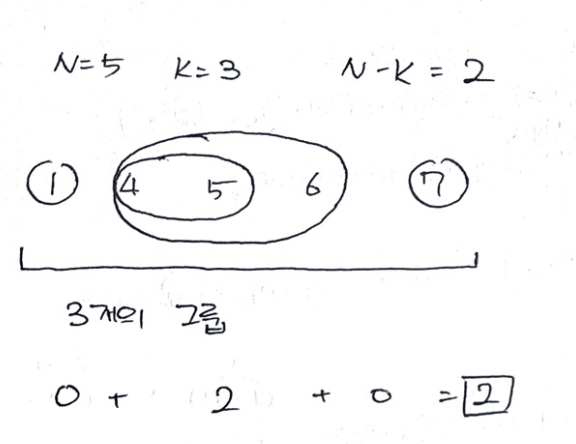
예시로 따지자면, 정렬된 차의 2개 합을 구했기 때문에 (4,5), (5,6)의 차를 구하게된것입니다.
즉 3개의 그룹을 만들고 N-K == 5-3 = 2인 2개의 차를 구해 최소합을 구할 수 있게 됩니다.
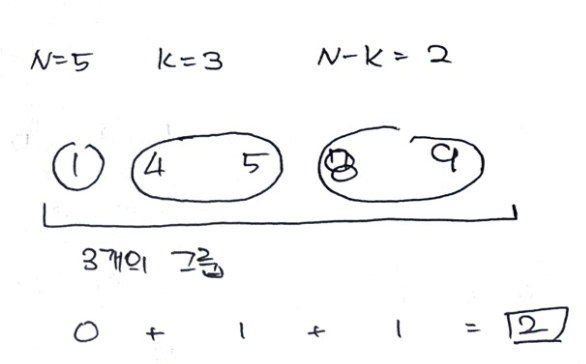
꼭 연속적인 수의 그룹이 아니더라도 3개의 그룹을 만들기 위해 2개의 차의 합을 구한다면 1,4,5,8,9인 경우 위와같은 그룹이 구성되게 됩니다.
Code
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
static int N;
static int K;
static int[] students;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine()," ");
N = Integer.parseInt(st.nextToken());
K = Integer.parseInt(st.nextToken());
students = new int[N];
st = new StringTokenizer(br.readLine()," ");
for(int i=0;i<N;i++){
students[i] = Integer.parseInt(st.nextToken());
}
int[] arr = new int[N-1];
for(int i=0;i<N-1;i++){
arr[i] = students[i+1]-students[i];
}
Arrays.sort(arr);
int result = 0;
for(int i=0;i<N-K;i++){
result += arr[i];
}
bw.write(String.valueOf(result));
bw.flush();
bw.close();
}
}Resulte
이 문제 유형의 핵심은 인접한 요소들을 그룹화 했을때, 각 그룹에서 가장 큰 값과 작은 값의 차가 최소가 되는것 인것 같습니다.
그리고 추가적인 조건은 그룹에 하나의 값을 가질 경우 해당 그룹의 차는 0이 되는 것입니다.
