11403 경로 찾기 : https://www.acmicpc.net/problem/11403
Problem
Solve
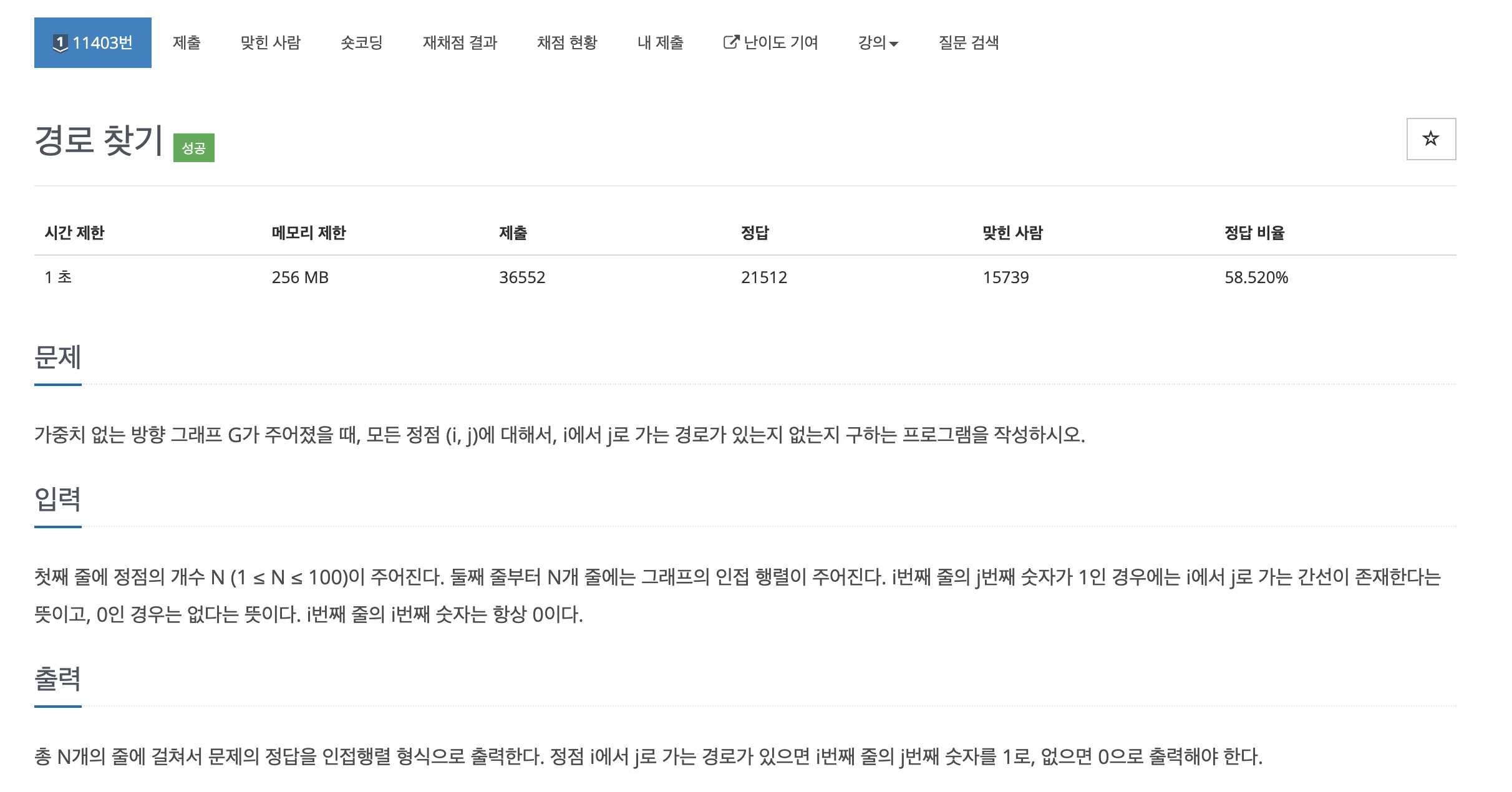
가중치 없는 방향 그래프가 주어졌을때, i정점에서 j정점까지 이동가능 여부의 배열을 반환하는 문제입니다.
방향 그래프라는 단어를 못봐서 조금 방황하긴 했는데, 문제를 보고 플로이드 와샬을 떠올렸습니다.
모든 정점에서 모든 정점까지 이동하는데 k정점을 지나가는 경우를 찾으면 됩니다.
즉, i정점에서 j정점으로 이동할수 있는지 확인하는데 k정점을 지나면서 지나갈수 있는지 확인해야합니다.
G[i][k]==1 && G[k][j]==1인 경우 G[i][j]=1이 되는겁니다.
플로이드 와샬은 3개의 반복문을 사용해야하는데, 정점의 개수가 최대 100이므로 O(N^3)으로 해결할 수 있습니다.
플로이드 와샬말고 다른 방법은 없을까 고민하다가 다익스트라 방법으로도 풀수 있을것 같아서 풀어봤는데, 풀고나니 다익스트라는 아니고 그냥 BFS 같습니다. ^^;
인접리스트를 이용해서 각 정점을 시작으로 모든 인접리스트를 확인하는 방법을 사용했으므로 O(N^2)로 풀은것 같은데.. 시간은 비슷하네요..(아님 복잡도 계산을 잘못했거나..)
Code
플로이드와샬
import java.io.*;
import java.util.StringTokenizer;
public class Main{
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Integer.parseInt(br.readLine());
int[][] G = new int[N][N];
for(int i=0;i<N;i++){
StringTokenizer st = new StringTokenizer(br.readLine()," ");
for(int j=0;j<N;j++){
G[i][j] = Integer.parseInt(st.nextToken());
}
}
makeGraph(G, N);
StringBuilder sb = new StringBuilder();
for(int i=0;i<N;i++){
for(int j=0;j<N;j++){
sb.append(G[i][j]).append(" ");
}
sb.append("\n");
}
bw.write(sb.toString());
bw.flush();
bw.close();
}
static void makeGraph(int[][] G, int N){
for(int k=0;k<N;k++){
for(int i=0;i<N;i++){
for(int j=0;j<N;j++){
if(G[i][k]==1 && G[k][j]==1) G[i][j]=1;
}
}
}
}
}BFS
import java.io.*;
import java.util.StringTokenizer;
import java.util.List;
import java.util.ArrayList;
import java.util.Queue;
import java.util.LinkedList;
public class Main{
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Integer.parseInt(br.readLine());
List<List<Integer>> G = new ArrayList<>();
for(int i=0;i<N;i++){
G.add(new ArrayList<>());
}
for(int i=0;i<N;i++){
StringTokenizer st = new StringTokenizer(br.readLine()," ");
for(int j=0;j<N;j++){
int node = Integer.parseInt(st.nextToken());
if(node == 1){
G.get(i).add(j);
}
}
}
int[][] graph = new int[N][N];
for(int i=0;i<N;i++){
dijkstra(G, N, graph, i);
}
StringBuilder sb = new StringBuilder();
for(int i=0;i<N;i++){
for(int j=0;j<N;j++){
sb.append(graph[i][j]).append(" ");
}
sb.append("\n");
}
bw.write(sb.toString());
bw.flush();
bw.close();
}
static void dijkstra(List<List<Integer>> G, int N, int[][] graph, int start){
Queue<Integer> queue = new LinkedList<>();
boolean[] visit = new boolean[N];
queue.offer(start);
while(!queue.isEmpty()){
int current = queue.poll();
for(int link : G.get(current)){
if(!visit[link]){
queue.offer(link);
visit[link] = true;
graph[start][link] = 1;
}
}
}
}
}
