프로그래머스 - 멀쩡한 사각형

leehyunjon·2022년 8월 17일

수학 프로그래머스

Algorithm

목록 보기

101/162

멀쩡한 사각형 : https://school.programmers.co.kr/learn/courses/30/lessons/62048

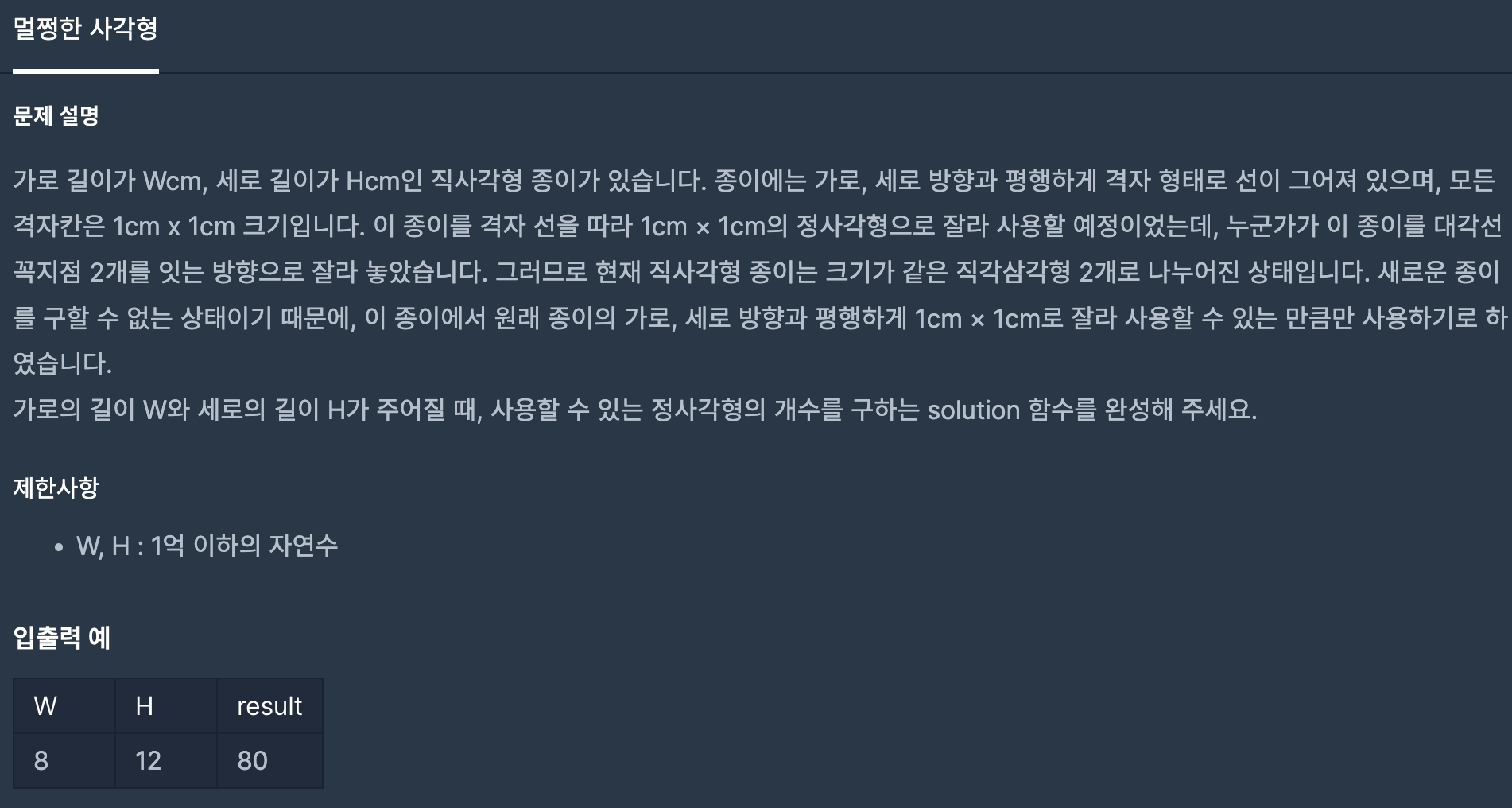
Problem

Solve

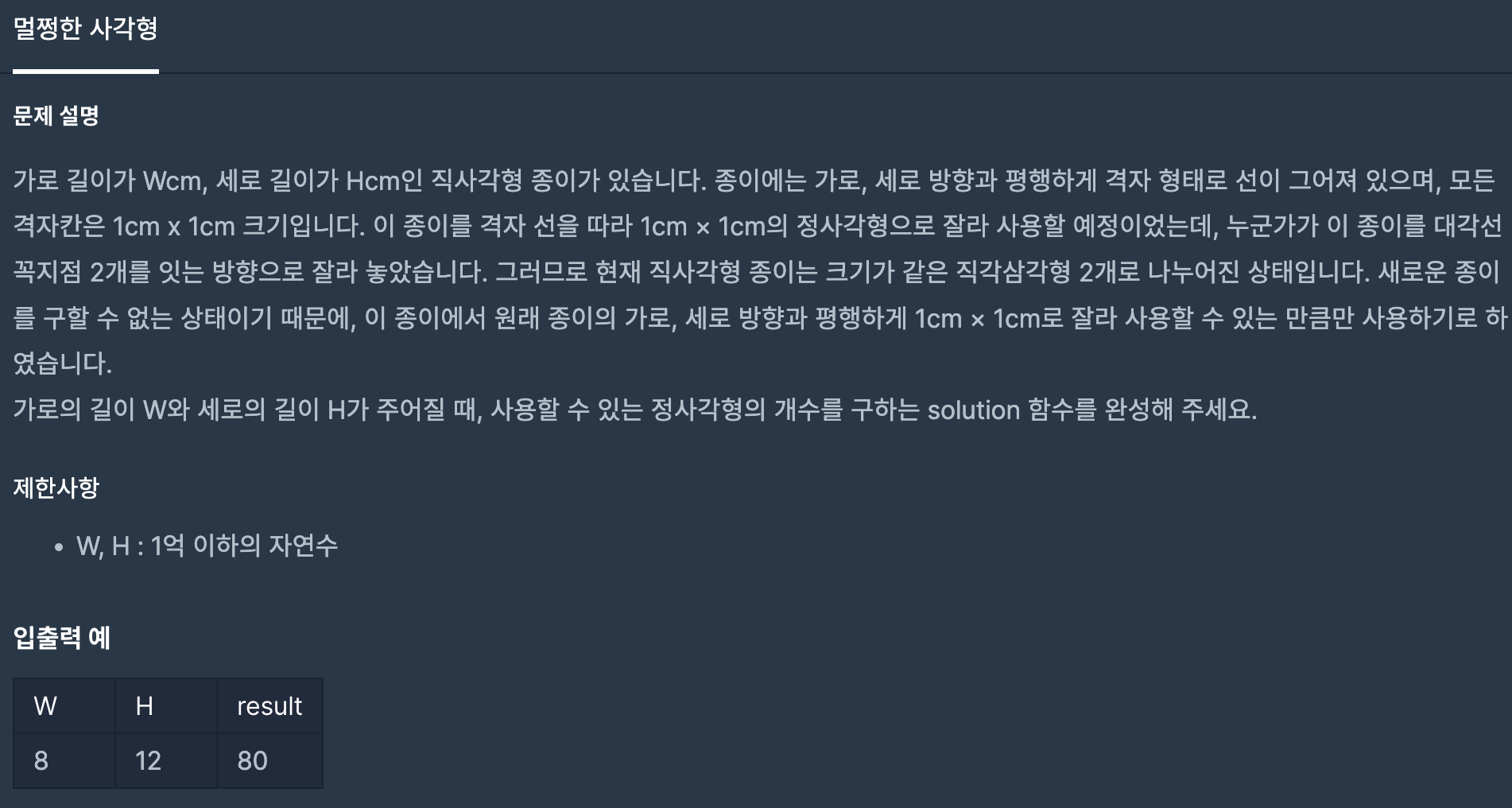
가로 w, 세로 h가 주어지고 꼭짓점에서 대각선 꼭짓점까지 선을 이었을때 선이 지나가는 정사각형을 제외한 나머지 정사각형의 개수를 구하는 문제

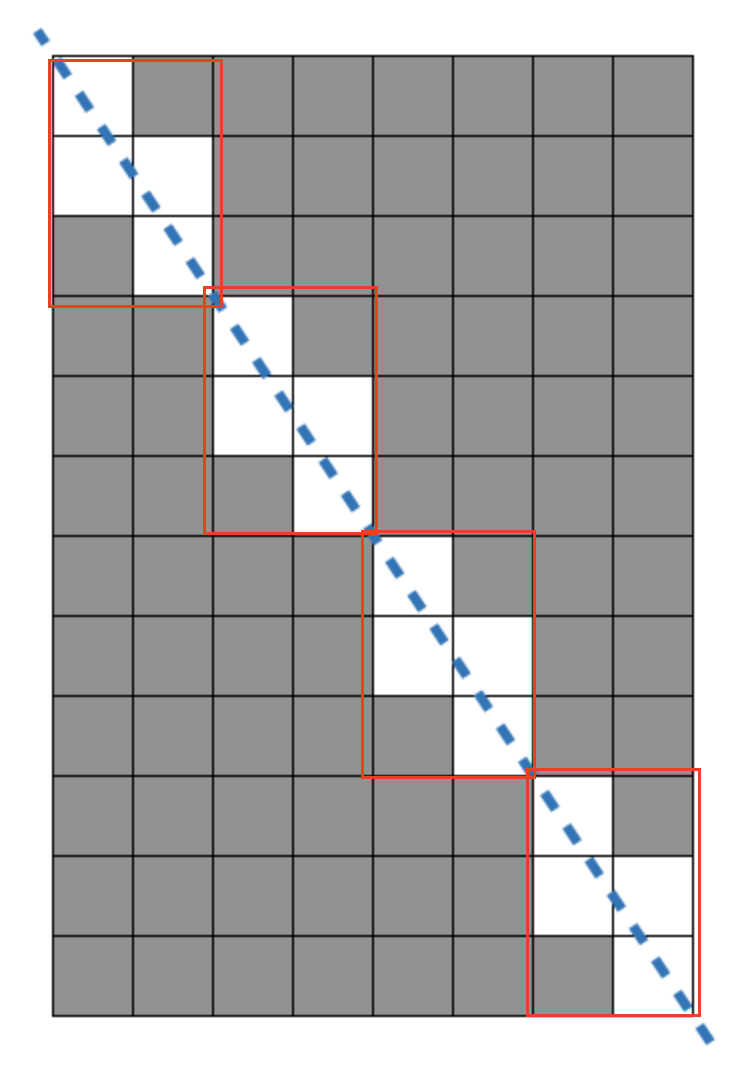
w : 8, h : 12일때 선분을 긋게 되면 (2,3), (4,6), (6,9), (8, 12)를 기준으로 동일한 패턴이 나타나게 된다.

이 패턴은 동일한 가로와 세로의 크기를 나타내는데, 이는 가로와 세로의 최대 공약수(GCD)로 나눈 크기가 된다.

GCD는 4가 되고 패턴 가로 : 8/4=2, 패턴 세로 : 12/4 = 3 으로 패턴의 크기가 만들어지고
각 패턴에서 사용할 수 있는 정사각형의 개수는 패턴의 세로 + 패턴의 가로 -1가 된다.

그리고 패턴의 개수는 GCD이기 때문에 식을 세울수 있다.
(w*h) - ((w/gcd + h/gcd -1)) * gcd

Code

public class 멀쩡한사각형 {
	public static void main(String[] args) {
		int w = 8;
		int h = 12;
		System.out.println(solution(w,h));
	}

	static public long solution(int w, int h){
		int gcd = getGcd(Math.max(w,h), Math.min(w,h));
		return ((long)w *h)-(((long)w/gcd+h/gcd-1)*gcd);
	}

	//gcd 구하기
	static public int getGcd(int a, int b){
		if(a%b==0) return b;
		else return getGcd(b, a%b);
	}
}