Norm

• 벡터의 크기를 측정하는 방법
• 두 벡터의 거리를 계산한다고도 볼 수 있음 (두 벡터의 차이를 구하는 과정이기에)
• 다양한 방법으로 크기를 측정할 수 있지만, L1 방법과 L2 방법만 기술할 예정

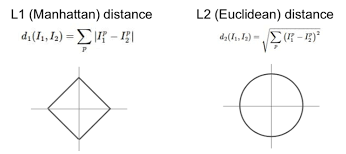
L1 Norm

정의

• 벡터의 각 성분끼리 차이의 절댓값의 합

해석

• 벡터의 각 축을 따라 이동하는 총 거리
• (예시) 2차원 평면에서 두 점 사이의 L1 거리는 각 점에서 x축과 y축을 따라 움직여서 도달하는 직각 경로의 합
• 맨해튼 거리, 택시캡 거리 라고도 함

L2 Norm

정의

• 벡터의 각 성분끼리 차이의 제곱값들의 합에 루트 씌운 값

해석

• 벡터끼리 떨어진 직선거리
• (예시) 2차원 평면에서 두 점 사이의 L2 거리는 각 점에서 목표 지점까지 그은 직선 경로
• 유클리드 거리

Loss

• 실제값과 예측값의 차이

L1 Loss

• L1 Norm 공식에 두 벡터 값으로 실제값과 예측값만 넣은 것
• Least Absolute Errors(LAE)라고도 불리며, 이 값을 데이터 수로 나누기만(평균) 하면 Mean Absolute Errors(MAE) 이기에, L1 Loss = MAE 동치이다
• (장점) L2 Loss에 비해 outlier의 영향을 덜 받고, robust함
• (단점) 절댓값 함수이기에, 0에서 미분 불가능

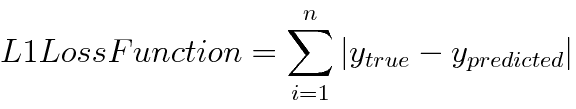
L2 Loss

• L2 Norm 공식에 두 벡터 값으로 실제값과 예측값만 넣은 것
• Least Squared Errors(LSE)라고도 불리며, 이 값을 데이터 수로 나누기만(평균) 하면 Mean Squared Errors(MSE) 이기에, L2 Loss = MSE 동치이다
• (장점) 제곱 함수이기에, 모든 구간에서 미분이 가능함
• (단점) 제곱을 취하기에, L1 Loss에 비해 outlier의 영향을 더 받음

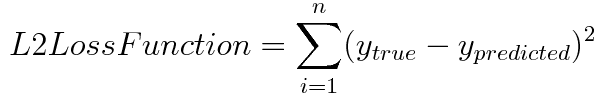
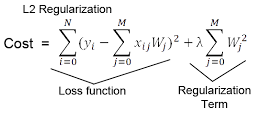
Regularization

• 정규화, 골고루 학습을 할 수 있도록 General하게 만들어줌
• 실제값 y, 예측값 xW (input x에 선형변환 W 적용해서 실제값 y에 가깝게 만드는 것이 목표)
• 이를 위한 Weight를 Update하는 과정을 W - grad = W_update 라고 가정하며, grad는 loss function의 미분값으로 사용

L1 Regularization

• 예측값과 실제값이 거의 똑같아져서 최종 Loss가 Regularization Term에 매우 강하게 의존한다고 가정할 때, 학습을 위해 Regularization Term을 미분을 하면(=gradient) 상수항만 남게 된다. 그럼 W를 update 할 때, 상수항이 W 값과 똑같아진다면, update된 W값은 0이 된다.
• 즉, 불필요한 Feature에 대응하는 Weight를 정확히 0으로 만들어버려, Feature selection의 효과를 냄
• L1 Regularization을 사용하는 선형 회귀 모델을 Lasso model이라고 함

Example

• W값이 1이라고 가정하고 regularization term "|W|" 을 미분하면 1 or -1 (상수term)
• Weight를 Update하게 되면 W_update = W - grad = W - 상수term 으로, 학습을 계속해서 상수term이 W와 같아지게 된다면 W값이 0이 된다.

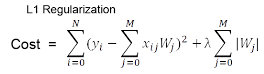
L2 Regularization

• 예측값과 실제값이 거의 똑같아져서 최종 Loss가 Regularization Term에 매우 강하게 의존한다고 가정할 때, 학습을 위해 Regularization Term을 미분을 해도(=gradient) 자기 자신(W) Term이 남아있기에, W값은 0이 될 수 없다.
• 즉, 불필요한 Feature(이상치)에 대응하는 Weight를 0에 가깝게 만들 뿐, 0으로 만들지는 않음
• 극단적으로 불필요한 Feature를 제거해버리는 L1과는 달리, L2가 일반화 성능이 높음
• L2 Regularization을 사용하는 선형 회귀 모델을 Ridge model이라고 함

Example

• W값이 1이라고 가정하고 regularization term "W^2" 을 미분하면 2W (자기 자신이 남음)
• Weight를 Update하게 되면 W_update = W - grad = W - 2W = -W 로, 아무리 학습을 진행해도 W 값은 0이 될 수 없다