[AI Deep Dive] Probabilty & Likelyhood

Probability vs Likelyhood

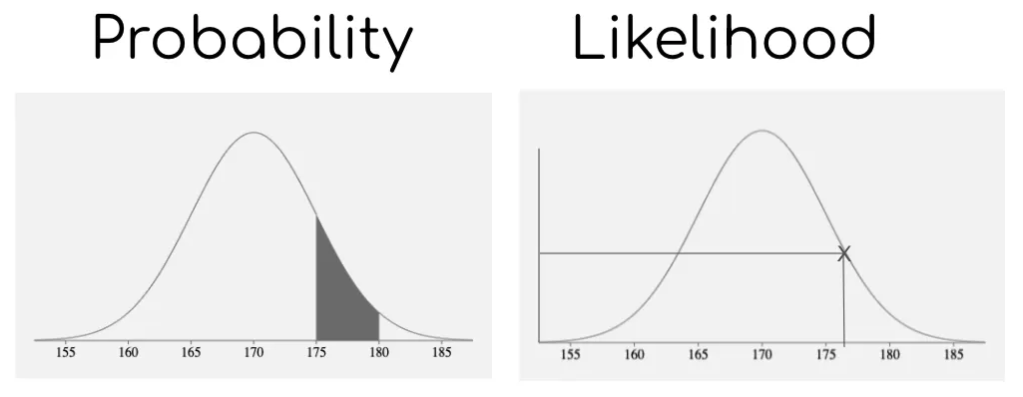
Probability

• 확률 분포가 고정된 상태에서 관측되는 사건이 변화될 때, 확률을 표현하는 단어

Likelyhood

• 관측된 사건이 고정된 상태에서 확률 분포가 변화될 때, 확률을 표현하는 단어

Next Token Prediction (NLP)

• Next token prediction은 토큰이 나올 확률(Probability)을 구하여 예측한 토큰을 포함한 문장(시퀀스)이 나올 확률(Likelyhood)을 최대화하는 문제

Probability

• "The cat is" 다음에 올 토큰(??)을 예측하는 문제
• "The cat is"라는 문맥 또는 시퀀스(확률 분포 고정)가 주어졌을 때, 다음 토큰(ex. "sleeping", "on", "happy" 등)이 나올 조건부 확률을 계산(관측되는 사건 변화 -> ?? 는 모르는 상태이므로 계속해서 변화)
• 토큰들에 대한 조건부 확률들은 모델의 Weight에 의존하며, 각 토큰의 출현 가능성을 나타냄.

Likelyhood (MLE)

• "The cat is sleeping" 자체는 이미 발생한 사건(관측된 사건 고정)
• "The cat is sleeping" (관측된 사건 고정) 에서 모델의 Weight(확률 분포의 변화)가 "The cat is sleeping" 을 생성할 확률을 최대화.
• 이를 Maximum Likelyhood Estimation (MLE) 라고 함.
• ?? 에 sleeping 이라는 단어가 나올 확률을 높이도록 함.

Summary

• Probability는 "The cat is"라는 주어진 문맥에 기반하여 다음 토큰의 출현 빈도를 예측하는 것
• Likelyhood는 이러한 예측(사건 고정)이 어떻게 모델 파라미터(확률 분포 변화)에 의존하는지를 보여줌.
  특정 파라미터 값에 대해 관측된 데이터(ex. "The cat is sleeping")가 발생할 확률을 최대화하며, 이를 통해 모델 파라미터를 조정하는 데 사용됨

Loss Function

• 실제 학습 과정은 Cross entropy 에 근사하여 loss를 계산.
• Probability -> Likelyhood (MLE) -> Negative Log Likelyhood (NLL) -> Cross Entropy (CE) 로 근사하여 실제 학습 Loss function 을 설계.

Negative Log Likelyhood (NLL)

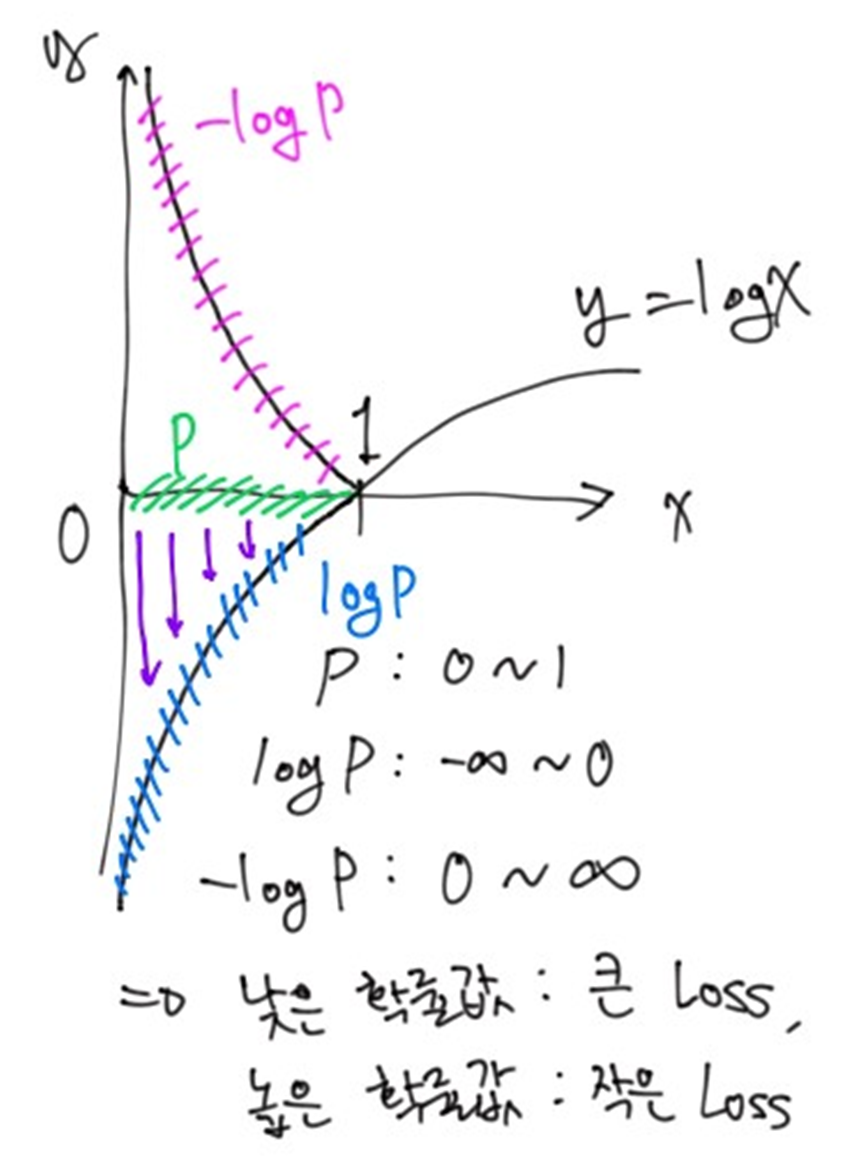
• 확률은 0~1값임. 그렇기에 확률을 직접 사용(MLE)할 경우, 확률 값이 매우 작아지는 경우도 존재함. 매우 작은 값을 다루는 것은 모델에서 매우 불안정함.
• 확률값을 로그로 변환하여 -무한대 ~ 0 사이 값으로 스케일링 해줌. 로그 스케일링을 진행하면 매우 작은 확률값이 매우 큰 음수값으로 변환됨. 결국, 매우 작은 확률값을 가지는 요소들도 모델 학습에 기여가 가능해짐.
• 음수를 취해줌으로써, 0 ~ 무한대 값으로 변환해줌. 결국 NLL을 loss function으로 사용하게 되면 매우 작은 확률값은 매우 큰 수, 아주 높은 확률은 0에 가깝게 변환됨. 매우 작은 확률을 가지는 요소들은 큰 loss값을 내뱉게 된다는 의미이며, 매우 높은 확률을 가지는 요소들은 작은 loss값을 뱉는다는 의미.
• 즉, negative log를 취해줌으로써 낮은 확률값일수록 더욱 큰 error를 부여한다는 의미.

Cross Entropy (CE)

• 모델이 출력한 확률 분포(각 토큰의 예측 확률)와 실제 토큰의 분포 사이의 차이를 계산. 이를 통해 모델이 실제 데이터의 분포를 얼마나 잘 반영하고 있는지를 평가.
• 즉, 예측 확률 분포와 실제 확률 분포의 차이를 계산

Loss Function Summary

Probability -> Likelyhood (MLE) -> Negative Log Likelyhood (NLL) -> Cross Entropy (CE)

NLL Loss vs CE Loss

NLL Loss

• 모델의 출력이 로그 확률(log-softmax) 형태일 때 사용하는 손실 함수. 즉, 이미 output이 확률인 경우에 사용.
• logits는 모델의 최종 Raw Output을 의미.
• loss = nn.NLLLoss(nn.log_softmax(logits), labels)

CE Loss

• 모델의 출력이 확률분포가 아닌 logits 형태일 때 사용하는 손실 함수.
• loss = nn.CrossEntropyLoss(logits,labels)