[백준] 1697 숨바꼭질

문제

수빈이는 동생과 숨바꼭질을 하고 있다. 수빈이는 현재 점 N(0 ≤ N ≤ 100,000)에 있고, 동생은 점 K(0 ≤ K ≤ 100,000)에 있다. 수빈이는 걷거나 순간이동을 할 수 있다. 만약, 수빈이의 위치가 X일 때 걷는다면 1초 후에 X-1 또는 X+1로 이동하게 된다. 순간이동을 하는 경우에는 1초 후에 2*X의 위치로 이동하게 된다.

수빈이와 동생의 위치가 주어졌을 때, 수빈이가 동생을 찾을 수 있는 가장 빠른 시간이 몇 초 후인지 구하는 프로그램을 작성하시오.

입력

첫 번째 줄에 수빈이가 있는 위치 N과 동생이 있는 위치 K가 주어진다. N과 K는 정수이다.

출력

수빈이가 동생을 찾는 가장 빠른 시간을 출력한다.

예제 입력

5 17

예제 출력

4

풀이

구하고자 하는 건 수빈이가 동생을 찾을 수 있는 "가장 빠른 시간"이 몇 초 후인지 이다.
여기서 bfs로 풀어야 한다는 것을 캐치했어야 했다.

나는 처음에 dfs로 탐색하면서 동생에게 가장 빠른 시간 내 도달한 값을 전역 변수(min)로 두고 모든 dfs 케이스의 결과에 대해 min과 비교하고자 했다. 결과적으로 아래와 같이 코드가 복잡하고 이해하기 어려울 뿐더러 옳게 동작하지도 않았다. 특히 수빈이가 왼쪽으로 한칸 이동하는 dfs 탐색은 무한재귀가 발생했다.

dfs로 풀고자 시도한 코드(오답)

cnt = 0
min = -1
def dfs(s, d, cnt):
    global min
    if s == d:
        print("동생에게 도착, 종료")
        if min == - 1: min = cnt
        elif cnt < min: min = cnt
        return min

    # 조건부 이동(지금까지 이동 횟수 < 최소 이동 횟수)
    if min != -1 and min < cnt: return 
    cnt+=1
    # 동생이 수빈이보다 왼쪽
    if d < s: 
        print("동생이 수빈이보다 왼쪽에 있음, x-1 이동")
        return dfs(s-1, d, cnt)
    # 동생이 수빈이보다 오른쪽
    elif s < d and s >= 0:
        print("동생이 수빈이보다 오른쪽에 있음")
        dfs(s-1, d, cnt) # 이거 고쳐야함
        dfs(s+1, d, cnt)
        dfs(s*2, d, cnt)

이후 bfs 로 풀어야 함을 깨달았고, 한참을 고민하다가 큐를 2개 이용하는 방법을 생각했다. 방법은 다음과 같다.

방법
1. 큐1의 모든 노드를 꺼내어 동생의 위치와 동일한지 확인하고(동일하면 bfs종료), 동일하지 않다면 해당 원소의 방문하지 않은 모든 인접 원소들을 큐2에 넣고 방문처리한다.
2. 이동 횟수를 1 증가시킨다.
3. 큐2 내부의 모든 원소를 큐1으로 옮기고 큐2를 비운다
4. 위 과정을 반복한다.

그림으로 보면 아래와 같다. 예시로 수빈이 위치: 1, 동생 위치: 5 로 하였다.
(그림에 잘못 표시함, 8은 꺼내지지 않고 그전에 5일때 종료하게 됨)

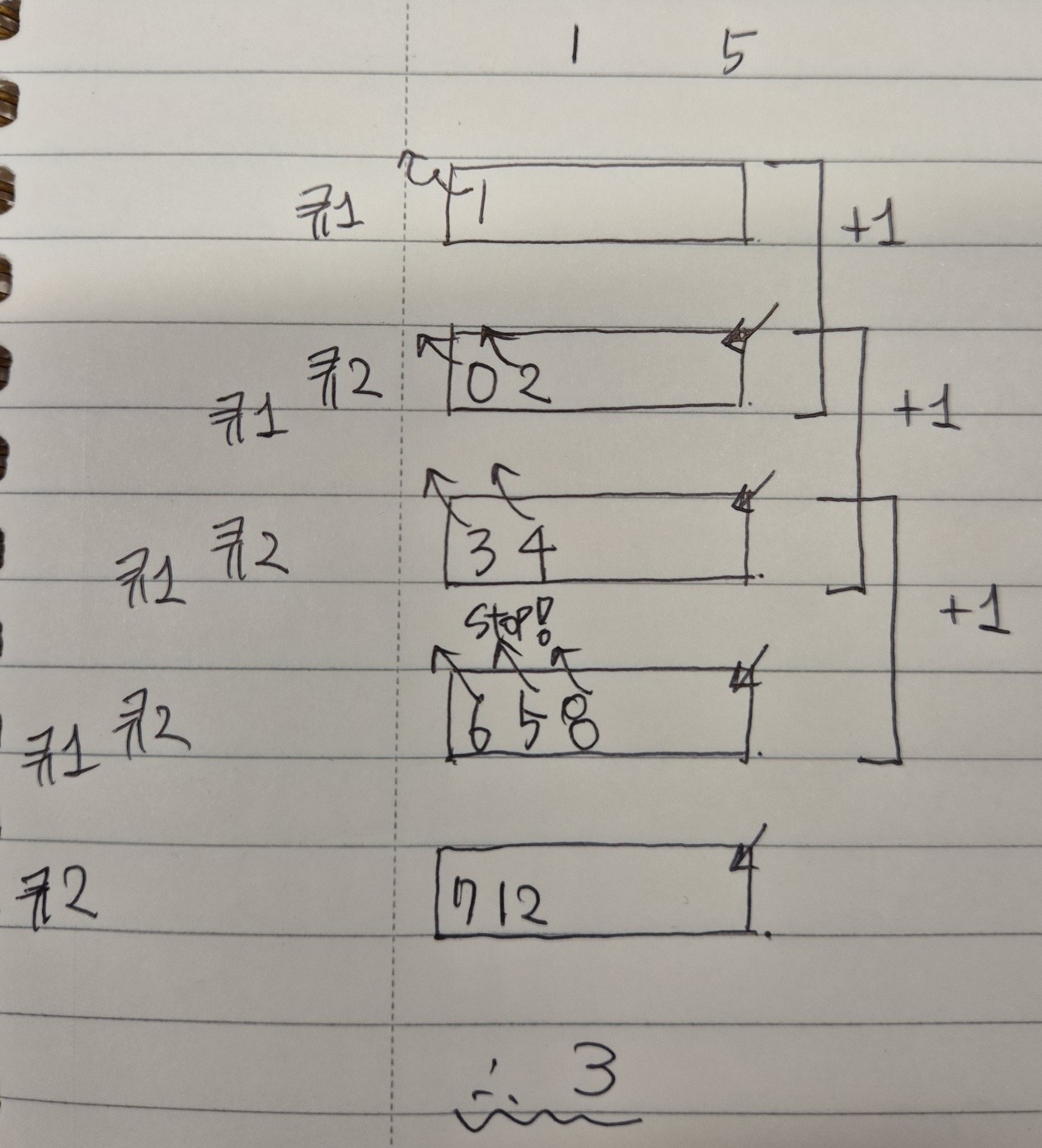
bfs 를 이용한 첫번째 풀이(큐 2개 이용)

import sys
input = sys.stdin.readline
from collections import deque

s, d = map(int, input().split())
cnt = 0
visited = [0]*100001
def bfs(s,d):
    global cnt
    queue1 = deque()
    queue2 = deque()

    queue1.append(s)
    visited[s] = 1 # 방문 표시
    while queue1:
        # 큐1에 있는 모든 노드들 꺼내서 bfs 수행
        for _ in range(len(queue1)):
            v = queue1.popleft()
            if v == d: return # 현재 위치가 동생위치라면 멈춤
            # 그게 아니라면 방문 안한 인접 노드들 모두 큐2 에 넣음
            else:
                if(v-1 >= 0 and visited[v-1] == 0): 
                    queue2.append(v-1)
                    visited[v-1] = 1
                if(v+1 <= 100000 and visited[v+1] == 0): 
                    queue2.append(v+1)
                    visited[v+1] = 1
                if(2*v <= 100000 and visited[2*v] == 0): 
                    queue2.append(2*v)
                    visited[2*v] = 1
        queue1 = queue2.copy()
        queue2.clear()
        cnt+=1

bfs(s,d)
print(cnt)

주의 사항

• 범위가 N(0 ≤ N ≤ 100,000), K(0 ≤ K ≤ 100,000) 이므로 방문 여부를 나타내는 배열의 길이는 100,001 이상이어야 한다.

bfs 를 이용한 두번째 풀이(큐 1개 사용)

큐 2개로 풀었지만 아무래도 일반적인 방법은 아닌 것 같아서 큐 1개를 사용해서 풀어보았다. 결과적으로는 훨씬 간결해졌고 이해하기도 편하다. 첫번째 풀이와의 차이점은 다음과 같다

첫번째 풀이: 큐 2개 사용, visited 배열은 0(방문X), 1(방문O) 을 사용
두번째 풀이: 큐 1개 사용, visited 배열은 0(방문X), N(해당 인덱스까지 걸린 이동 횟수)

생각해보면 bfs 를 이용해 최단거리를 계산할때는 큐1개와 직전노드까지 걸린 이동 거리를 이용했었다. 예를 들면 2차원 좌표에서 특정 지점까지 가는 최단 거리를 구하는 문제는 큐1개와 방문 처리를 나타내는 배열(arr[x][y] = 직전 노드까지 걸린 이동 횟수) 를 이용했었다.

문제를 풀기전에 어떤 방식으로 어떻게 풀어야 할지 천천히 고민해보고 풀어보아야겠다.

import sys
input = sys.stdin.readline
from collections import deque

s, d = map(int, input().split())

def bfs(s,d):
    visited = [0] * 100001
    queue = deque()
    queue.append(s)
    visited[s] = 0

    while queue:
        for _ in range(len(queue)):
            v = queue.popleft()
            if v == d:
                print(visited[v])
                return
            for n in (v-1,v+1,2*v):
                if n>=0 and n<=100000 and visited[n] == 0: 
                    queue.append(n)
                    visited[n] = visited[v] + 1

bfs(s,d)