[백준] (실패) 10423 전기가 부족해

문제

세계에서 GDP가 가장 높은 서강 나라는 소프트웨어와 하드웨어 기술이 모두 최고라서 IT강국이라 불리고, 2015년부터 세상에서 가장 살기 좋은 나라 1등으로 꼽히고 있다.

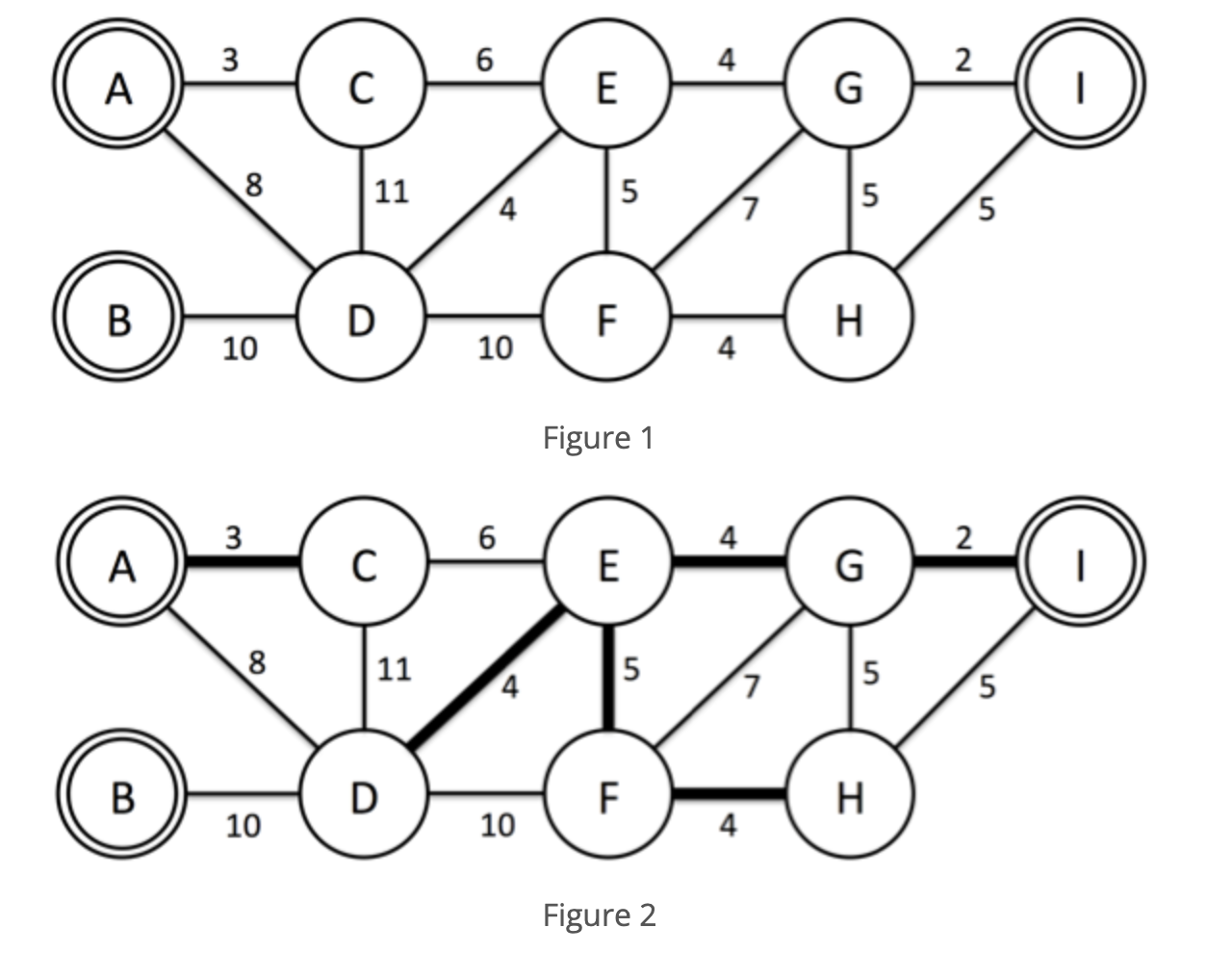
살기 좋은 나라 1등으로 꼽힌 이후 외국인 방문객들이 많아졌고, 그에 따라 전기 소비율이 증가하여 전기가 많이 부족한 상황이 되었다. 따라서 서강 나라의 대통령은 최근 개발이 완료된 YNY발전소 프로젝트를 진행 하기로 하였다. 발전소를 만들 때 중요한 것은 발전소 건물과 도시로 전기를 공급해 줄 케이블이다. 발전소는 이미 특정 도시에 건설되어 있고, 따라서 추가적으로 드는 비용은 케이블을 설치할 때 드는 비용이 전부이다. 이 프로젝트의 문제는 케이블을 설치할 때 드는 비용이 굉장히 크므로 이를 최소화해서 설치하여 모든 도시에 전기를 공급하는 것이다. 여러분은 N개의 도시가 있고 M개의 두 도시를 연결하는 케이블의 정보와 K개의 YNY발전소가 설치된 도시가 주어지면 케이블 설치 비용을 최소로 사용하여 모든 도시에 전기가 공급할 수 있도록 해결해야 한다. 중요한 점은 어느 한 도시가 두 개의 발전소에서 전기를 공급받으면 낭비가 되므로 케이블이 연결되어있는 도시에는 발전소가 반드시 하나만 존재해야 한다. 아래 Figure 1를 보자. 9개의 도시와 3 개의 YNY발전소(A,B,I)가 있고, 각각의 도시들을 연결할 때 드는 비용이 주어진다.

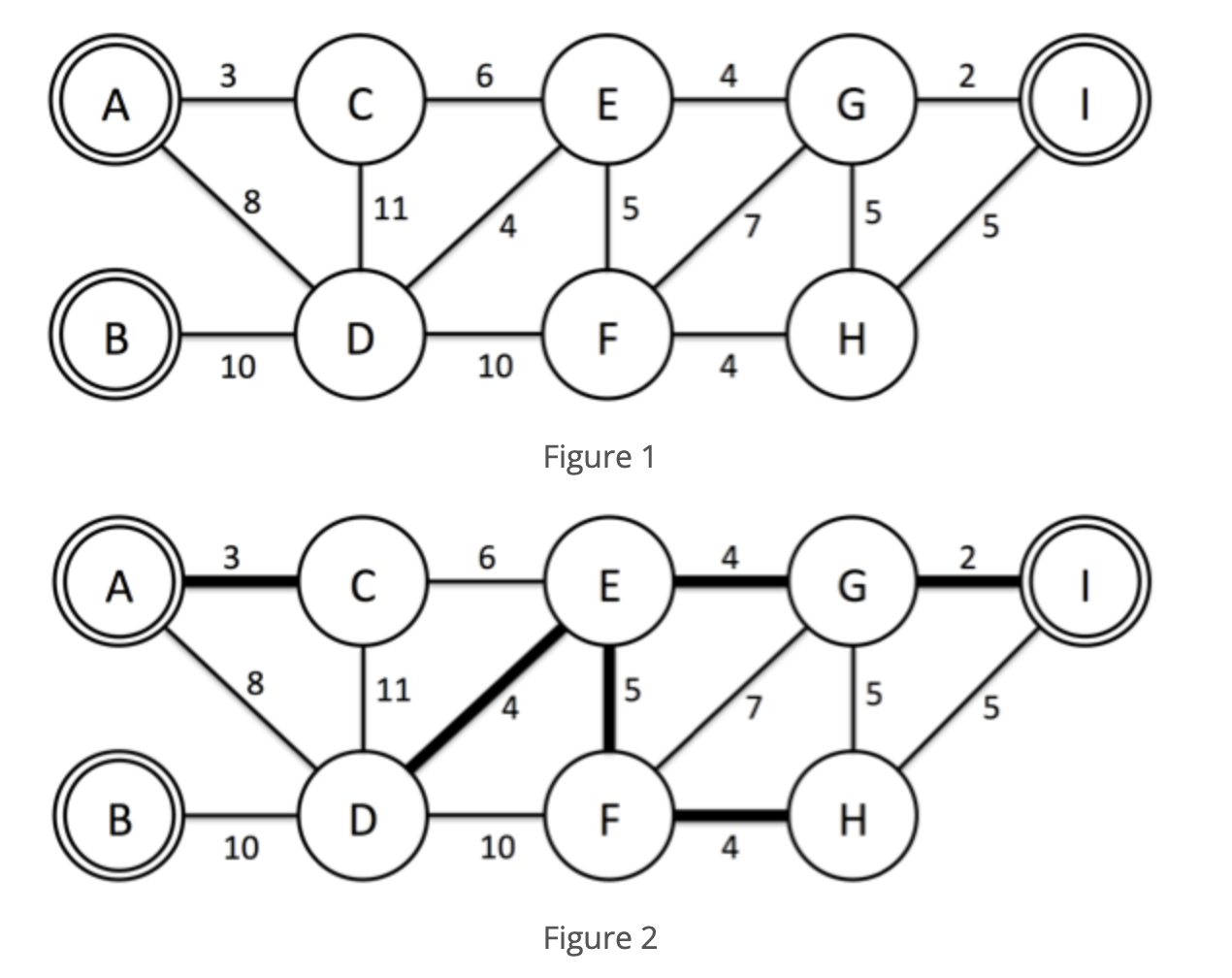
이 예제에서 모든 도시에 전기를 공급하기 위하여 설치할 케이블의 최소 비용은 22이고, Figure 2의 굵은 간선이 연결한 케이블이다. B 도시는 연결된 도시가 하나도 없지만, 발전소가 설치된 도시는 전기가 공급될 수 있기 때문에 상관없다.

입력

첫째 줄에는 도시의 개수 N(1 ≤ N ≤ 1,000)과 설치 가능한 케이블의 수 M(1 ≤ M ≤ 100,000)개, 발전소의 개수 K(1 ≤ K ≤ N)개가 주어진다. 둘째 줄에는 발전소가 설치된 도시의 번호가 주어진다. 셋째 줄부터 M개의 두 도시를 연결하는 케이블의 정보가 u, v, w로 주어진다. 이는 u도시와 v도시를 연결하는 케이블을 설치할 때 w의 비용이 드는 것을 의미한다. w는 10,000보다 작거나 같은 양의 정수이다.

출력

모든 도시에 전기를 공급할 수 있도록 케이블을 설치하는 데 드는 최소비용을 출력한다.

예제 입력 1

9 14 3
1 2 9
1 3 3
1 4 8
2 4 10
3 4 11
3 5 6
4 5 4
4 6 10
5 6 5
5 7 4
6 7 7
6 8 4
7 8 5
7 9 2
8 9 5

예제 출력 1

22

예제 입력 2

4 5 1
1
1 2 5
1 3 5
1 4 5
2 3 10
3 4 10

예제 출력 2

15

풀이

union 하기전에 사이클 생기는지 여부를 확인했어야 했는데, 이걸 안해서 왜 틀렸는지 끙끙댔다;;. 나중에 다시 풀어보자.

풀이 방법은 다음과 같다.
사이클이 생성되지 않음을 확인한 후, union 할지 여부를 판단하기 위해선 아래 3가지 경우를 고려해야 한다.
1. 정점(발전소 연결X) - 정점(발전소 연결X)
2. 정점(발전소 연결O) - 정점(발전소 연결O)
3. 정점(발전소 연결O) - 정점(발전소 연결O)
위 3가지 경우 중 1, 2번에 대해서만 연결을 해줘야 한다.

그리고 발전소가 모두 연결되어 있지 않은 정점에 대해서는 그냥 union, 발전소가 둘 중 하나가 연결되어 있는 경우는 연결되어 있지 않은 정점들이 속한 그룹에 대해 모두 발전소 연결 유무를 true 로 변경해준 후 union 을 진행한다.

설명을 보다시피, 나는 정점별로 발전소 연결 유무를 기록하기 위한 hasE 배열을 사용하였다.

이를 통해 정점 들간의 연결을 진행할때, 해당 정점이 발전소가 연결되어 있는지 유무를 파악할 수 있게된다.
*이렇게 푸는 방법보다, 루트 정점이 발전소를 보유하고 있는지 유무를 기록하면 좀 더 MST 풀이에 적합한 것 같다. 다음엔 이 방법으로 풀어보자.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.StringTokenizer;

class Edge implements Comparable<Edge>{
    int a;
    int b;
    int dist;

    public Edge(int a, int b, int dist){
        this.a = a;
        this.b = b;
        this.dist = dist;
    }

    @Override
    public int compareTo(Edge o) {
        return Integer.compare(this.dist, o.dist);
    }
}
public class Main {

    static int N;
    static int M;
    static int K;
    static int[] parent;
    static boolean[] hasE;
    static ArrayList<Edge> edges;
    static int sum;

    static int findP(int x){
        if(parent[x] != x) return parent[x] = findP(parent[x]);
        return parent[x];
    }
    static void union(int n1, int n2){
        int p1 = findP(n1);
        int p2 = findP(n2);

        if(p1 < p2) parent[p2] = p1;
        else parent[p1] = p2;
    }

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        // 도시 개수, 설치 가능한 케이블 수, 발전소 개수
        N = Integer.parseInt(st.nextToken());
        M = Integer.parseInt(st.nextToken());
        K = Integer.parseInt(st.nextToken());
        edges = new ArrayList<>();
        parent = new int[N+1];
        for(int i = 1; i <= N; i++) parent[i] = i;

        // 발전소 정보 얻기
        hasE = new boolean[N+1];
        String[] tmp = br.readLine().split(" ");
        // 자신과 연결된 발전소가 있는 경우 표시
        for(int i = 0; i < tmp.length; i++){
            int n = Integer.parseInt(tmp[i]);
            hasE[n] = true;
        }

        // 간선 정보 입력 받기
        for(int i = 1; i <= M; i++){
            st = new StringTokenizer(br.readLine());
            int u = Integer.parseInt(st.nextToken());
            int v = Integer.parseInt(st.nextToken());
            int w = Integer.parseInt(st.nextToken());
            edges.add(new Edge(u,v,w));
        }
        edges.sort(null);

        // union 시키기(둘 중에 하나만 연결되어 있거나, 모두 연결되어 있지 않은 경우)
        for (int i = 0; i < edges.size(); i++) {
            Edge e = edges.get(i);
            if(findP(e.a) == findP(e.b)) continue;
            // 둘 다 발전소 연결이 되어있는 경우는 continue
            if(hasE[e.a] && hasE[e.b]) {
                continue;
            }
            // a 가 발전소와 연결이 되어 있는 경우 -> b 와 연결된 그룹 모두 true
            if(hasE[e.a] && !hasE[e.b]){
                union(e.a, e.b);
                sum += e.dist;
                int p = findP(e.b);
                for(int j = 1; j <= N; j++){
                    // 같은 그룹인 경우 모두 발전소 연결되어 있다고 처리
                    if(findP(j) == p) hasE[j] = true;
                }
            }
            // b 가 발전소와 연결이 되어 있는 경우 -> a 와 연결된 그룹 모두 true
            else if(hasE[e.b] && !hasE[e.a]){
                union(e.a, e.b);
                sum += e.dist;
                int p = findP(e.a);
                for(int j = 1; j <= N; j++){
                    // 같은 그룹인 경우 모두 발전소 연결되어 있다고 처리
                    if(findP(j) == p) hasE[j] = true;
                }
            }
            // 둘 다 발전소와 연결되어 있지 않은 경우
            else{
                union(e.a, e.b);
                sum += e.dist;
            }
        }

        System.out.println(sum);

    }

}