문제
깽미는 24살 모태솔로이다. 깽미는 대마법사가 될 순 없다며 자신의 프로그래밍 능력을 이용하여 미팅 어플리케이션을 만들기로 결심했다. 미팅 앱은 대학생을 타겟으로 만들어졌으며 대학교간의 도로 데이터를 수집하여 만들었다.
이 앱은 사용자들을 위해 사심 경로를 제공한다. 이 경로는 3가지 특징을 가지고 있다.
사심 경로는 사용자들의 사심을 만족시키기 위해 남초 대학교와 여초 대학교들을 연결하는 도로로만 이루어져 있다.
사용자들이 다양한 사람과 미팅할 수 있도록 어떤 대학교에서든 모든 대학교로 이동이 가능한 경로이다.
시간을 낭비하지 않고 미팅할 수 있도록 이 경로의 길이는 최단 거리가 되어야 한다.
만약 도로 데이터가 만약 왼쪽의 그림과 같다면, 오른쪽 그림의 보라색 선과 같이 경로를 구성하면 위의 3가지 조건을 만족하는 경로를 만들 수 있다.
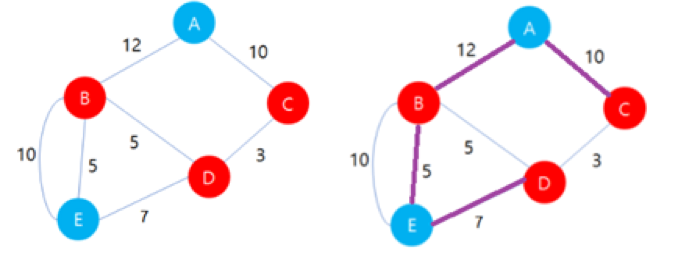
이때, 주어지는 거리 데이터를 이용하여 사심 경로의 길이를 구해보자.
입력
입력의 첫째 줄에 학교의 수 N와 학교를 연결하는 도로의 개수 M이 주어진다. (2 ≤ N ≤ 1,000) (1 ≤ M ≤ 10,000)
둘째 줄에 각 학교가 남초 대학교라면 M, 여초 대학교라면 W이 주어진다.
다음 M개의 줄에 u v d가 주어지며 u학교와 v학교가 연결되어 있으며 이 거리는 d임을 나타낸다. (1 ≤ u, v ≤ N) , (1 ≤ d ≤ 1,000)
출력
깽미가 만든 앱의 경로 길이를 출력한다. (모든 학교를 연결하는 경로가 없을 경우 -1을 출력한다.)
예제 입력
5 7
M W W W M
1 2 12
1 3 10
4 2 5
5 2 5
2 5 10
3 4 3
5 4 7
예제 출력
34
풀이
거의 다 왔는데,, MST 문제인걸 고려안하고 대학교 번호가 작은 것부터 union 해버렸다.
동일 정점 간에 여러 경로가 존재해서 이것들의 최솟값을 관리했는데,
이걸 처리하고 나니 마치 MST 로 푼것 마냥 착각해버렸다.
=> MST 는 비용이 작은 간선부터 먼저 연결해야한다!!!
풀이 1(실패) - 동일 정점들간 최소 값을 저장해서 비용을 고려하지 않고, 앞 번호(인덱스)부터 UNION
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.StringTokenizer;
public class Main {
static char[] gender;
static int[] parent;
static int sum_dist = 0;
static int[][] dist;
static int findP(int x) {
if(parent[x] != x) return parent[x] = findP(parent[x]);
return parent[x];
}
static void union(int n1, int n2, int newDist) {
sum_dist += newDist;
int p1 = findP(n1);
int p2 = findP(n2);
if(p1 < p2) parent[p2] = p1;
else parent[p1] = p2;
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken()); // 정점 개수
int M = Integer.parseInt(st.nextToken()); // 간선 개수
parent = new int[N+1];
gender = new char[N+1];
// 비열 비용 초기화(-1 로)
dist = new int[N+1][N+1]; // 학교별 최소 거리 기록용
for(int i = 1; i <= N; i++) {
for(int j = 1; j <= N; j++) {
dist[i][j] = -1;
}
}
// 학교별 남초/여초 정보 저장
st = new StringTokenizer(br.readLine());
for(int i = 1; i <= N; i++) {
char c = String.valueOf(st.nextToken()).charAt(0); // 바로 뽑는거 없나..?
gender[i] = c;
}
// parent 배열 초기화
for(int i = 1; i <= N; i++) {
parent[i] = i;
}
// M 개 간선정보 입력받음
// 여초-남초, 남초-여초 인 경우에만 기록
// 만약에 더 작은 인덱스를 키로 하는 값이 존재 O -> 더 작은 값으로 교체
// 존재 X -> 작은 인덱스를 키로 하고 값 바로 넣음
for(int i = 1; i <= M; i++) {
st = new StringTokenizer(br.readLine());
int f = Integer.parseInt(st.nextToken());
int s = Integer.parseInt(st.nextToken());
int d = Integer.parseInt(st.nextToken());
// 성별이 같거나 경우 -> pass
if(gender[f] == gender[s]) continue;
// 작은 인덱스 기준으로 값 관리
int sm = Math.min(f, s);
int lg = Math.max(f, s);
// 기존에 값이 기록되어 있으면 더 작은거 넣고
// 그렇지 않으면 그냥 넣음
if(dist[sm][lg] != -1) {
dist[sm][lg] = Math.min(dist[sm][lg], d);
}
else {
dist[sm][lg] = d;
}
}
// dist 배열 돌면서 union 진행
for(int i = 1; i <= N; i++) {
for(int j = 1; j <= N; j++) {
// 값이 존재하면, 즉 -1 이 아니면 union 처리
if(dist[i][j] != -1) {
union(i, j, dist[i][j]);
}
}
}
// 모든 학교를 연결하지 못한 경우 -1 을 출력
int fv = findP(parent[1]);
for(int i = 2; i <= N; i++) {
if(fv != findP(parent[i])) {
System.out.println("-1");
return;
}
}
// 모든 학교를 다 연결한 경우 dist 를 출력
System.out.println(sum_dist);
}
}풀이 2(성공) - 풀이 1에서 정점들 간 거리 작은 것부터 UNION, 이를 위해 Edge 클래스 사용 + Collections.sort 적용
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;
import java.util.StringTokenizer;
class Edge implements Comparable<Edge>{
int f;
int s;
int d;
public Edge(int f, int s, int d) {
this.f = f;
this.s = s;
this.d = d;
}
@Override
public int compareTo(Edge e) {
// TODO Auto-generated method stub
return Integer.compare(d, e.d);
}
}
public class Main {
static char[] gender;
static int[] parent;
static int sum_dist;
static int[][] dist;
static ArrayList<Edge> elist;
static int findP(int x) {
if(parent[x] != x) return parent[x] = findP(parent[x]);
return parent[x];
}
static void union(int n1, int n2, int newDist) {
sum_dist += newDist;
int p1 = findP(n1);
int p2 = findP(n2);
if(p1 < p2) parent[p2] = p1;
else parent[p1] = p2;
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken()); // 정점 개수
int M = Integer.parseInt(st.nextToken()); // 간선 개수
parent = new int[N+1];
gender = new char[N+1];
// 비열 비용 초기화(-1 로)
dist = new int[N+1][N+1]; // 학교별 최소 거리 기록용
for(int i = 1; i <= N; i++) {
for(int j = 1; j <= N; j++) {
dist[i][j] = -1;
}
}
// 학교별 남초/여초 정보 저장
st = new StringTokenizer(br.readLine());
for(int i = 1; i <= N; i++) {
char c = String.valueOf(st.nextToken()).charAt(0); // 바로 뽑는거 없나..?
gender[i] = c;
}
// parent 배열 초기화
for(int i = 1; i <= N; i++) {
parent[i] = i;
}
// M 개 간선정보 입력받음
// 여초-남초, 남초-여초 인 경우에만 기록
// 만약에 더 작은 인덱스를 키로 하는 값이 존재 O -> 더 작은 값으로 교체
// 존재 X -> 작은 인덱스를 키로 하고 값 바로 넣음
for(int i = 1; i <= M; i++) {
st = new StringTokenizer(br.readLine());
int f = Integer.parseInt(st.nextToken());
int s = Integer.parseInt(st.nextToken());
int d = Integer.parseInt(st.nextToken());
// 성별이 같은 경우 -> pass
if(gender[f] == gender[s]) continue;
// 작은 인덱스 기준으로 값 관리
int sm = Math.min(f, s);
int lg = Math.max(f, s);
// 기존에 값이 기록되어 있으면 더 작은거 넣고
// 그렇지 않으면 그냥 넣음
if(dist[sm][lg] != -1) {
dist[sm][lg] = Math.min(dist[sm][lg], d);
}
else {
dist[sm][lg] = d;
}
}
elist = new ArrayList<Edge>();
// dist 배열 돌면서 Edge 모음 배열에 넣음
for(int i = 1; i < N; i++) {
for(int j = i+1; j <= N; j++) {
// 값이 존재하면, 즉 -1 이 아니면 union 처리
if(dist[i][j] != -1) {
elist.add(new Edge(i, j, dist[i][j]));
}
}
}
// Edge 배열을 거리순으로 정렬
Collections.sort(elist, Comparator.naturalOrder());
// union 시작
for(int i = 0; i < elist.size(); i++) {
Edge g = elist.get(i);
if(findP(g.f) != findP(g.s)) {
union(g.f, g.s, g.d);
}
}
// 모든 학교를 연결하지 못한 경우 -1 을 출력
int fv = findP(parent[1]);
for(int i = 2; i <= N; i++) {
if(fv != findP(parent[i])) {
System.out.println("-1");
return;
}
}
// 모든 학교를 다 연결한 경우 sum_dist 를 출력
System.out.println(sum_dist);
}
}풀이 3(성공) - 풀이 2의 최적화 적용
1.dist[N][N] 2차원 배열은 필요 없음
간선 정보들에 대해 Edge 들을 만들고 모든 Edge 들에 대해 거리가 작은 순으로 정렬한 후 순회하며 사이클 여부를 검사하고 union 을 할건데, 이 과정에서 정점 간 경로가 여러 개 있어도 작은 것 기준으로 union 하고, 뒤에서는 이미 사이클이 생겨서 적용이 어차피 안되기 때문에 괜찮다.
2.union 함수 안에서 거리 더하기보단, 크루스칼 루프에서 더하기
union 은 union 고유의 기능만을 갖는게 좋다.
3.모든 정점 연결확인할 때 findP(parent[i]) 말고 findP(i) 쓰자. 불필요하게 복잡하다.
findP(i) 를 해도 결국 최장 부모를 찾게되므로, 불필요하게 복잡하다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;
import java.util.StringTokenizer;
class Edge implements Comparable<Edge>{
int f;
int s;
int d;
public Edge(int f, int s, int d) {
this.f = f;
this.s = s;
this.d = d;
}
@Override
public int compareTo(Edge e) {
// TODO Auto-generated method stub
return Integer.compare(d, e.d);
}
}
public class Main {
static char[] gender;
static int[] parent;
static int sum_dist;
static ArrayList<Edge> elist;
static int findP(int x) {
if(parent[x] != x) return parent[x] = findP(parent[x]);
return parent[x];
}
static void union(int n1, int n2, int newDist) {
int p1 = findP(n1);
int p2 = findP(n2);
if(p1 < p2) parent[p2] = p1;
else parent[p1] = p2;
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken()); // 정점 개수
int M = Integer.parseInt(st.nextToken()); // 간선 개수
parent = new int[N+1];
gender = new char[N+1];
// 학교별 남초/여초 정보 저장
st = new StringTokenizer(br.readLine());
for(int i = 1; i <= N; i++) {
char c = String.valueOf(st.nextToken()).charAt(0); // 바로 뽑는거 없나..?
gender[i] = c;
}
// parent 배열 초기화
for(int i = 1; i <= N; i++) {
parent[i] = i;
}
// M 개 간선정보 입력받음
// 여초-남초, 남초-여초 인 경우에만 기록
// 만약에 더 작은 인덱스를 키로 하는 값이 존재 O -> 더 작은 값으로 교체
// 존재 X -> 작은 인덱스를 키로 하고 값 바로 넣음
elist = new ArrayList<Edge>();
for(int i = 1; i <= M; i++) {
st = new StringTokenizer(br.readLine());
int f = Integer.parseInt(st.nextToken());
int s = Integer.parseInt(st.nextToken());
int d = Integer.parseInt(st.nextToken());
// 성별이 같은 경우 -> pass
if(gender[f] == gender[s]) continue;
elist.add(new Edge(f, s, d));
}
// Edge 배열을 거리순으로 정렬
Collections.sort(elist, Comparator.naturalOrder());
// union 시작
for(int i = 0; i < elist.size(); i++) {
Edge g = elist.get(i);
if(findP(g.f) != findP(g.s)) {
sum_dist += g.d;
union(g.f, g.s, g.d);
}
}
// 모든 학교를 연결하지 못한 경우 -1 을 출력
int fv = findP(1);
for(int i = 2; i <= N; i++) {
if(fv != findP(i)) {
System.out.println("-1");
return;
}
}
// 모든 학교를 다 연결한 경우 sum_dist 를 출력
System.out.println(sum_dist);
}
}