파라메트릭 서치(Parametric Search)

파라메트릭 서치(Parametric Search)

이분 탐색이 정렬된 배열에서 특정한 값의 위치를 찾거나 존재 유무를 파악하는데 사용된다면, 파라메트릭 서치는 정렬된 배열에서 조건을 만족하는 "최적의 값"을 찾는데 사용된다. 파라메트릭 서치는 주로 특정한 조건을 만족하는 최소 또는 최대의 값을 찾는 데 사용된다.

파라메트릭 서치는 최적의 값을 구하는 최적화 문제를 결정 문제(decision problem)로 바꿔 이분 탐색을 통해 해결한다. 결정 문제는 'True' or 'False'로 해결할 수 있는 문제를 말한다.

K개를 만족하는 랜선의 최대 길이를 구해야 할때, 최적화 문제를 다음과 같이 결정 문제로 변환할 수 있다.

랜선의 최대 길이를 구해라 -> 최적화 문제
현재 랜선의 길이로 K개의 랜선을 만들 수 있는가(True/False) -> 결정 문제

예시를 들어보자.

1654 랜선 자르기 문제를 파라메트릭 서치를 이용해 해결할 수 있다.

주어진 랜선들을 잘라 동일한 길이의 K개의 랜선을 만들려고 할때, 만들 수 있는 랜선의 최대 길이를 구하는 문제이다. *가능한 최대길이를 사용했을때 만들어지는 랜선의 개수가 K개 이상일때는 상관없다.

해결법부터 말하자면, 주어진 랜선들 중 최대 길이의 랜선의 길이에 대해 이분 탐색을 해나가며 중앙값을 주어진 랜선들에 모두 나눠주고, 각각의 몫을 합해 K개가 될 때, 기존 중앙값 보다 더 큰 길이를 사용했을때 몫의 합이 K개가 되는지 확인해주면 된다. 이처럼 조건(현재는 K개)를 만족시키는 "최적의 값"을 이분 탐색으로 찾아나가는 방법을 파라메트릭 서치라고 한다.

예를 들어 K가 6이고 주어진 랜선 5개의 길이가 425 539 743 12500 50000 라고 하자.

가장 긴 랜선인 50000에 대해 이분 탐색을 행하면 다음과 같다

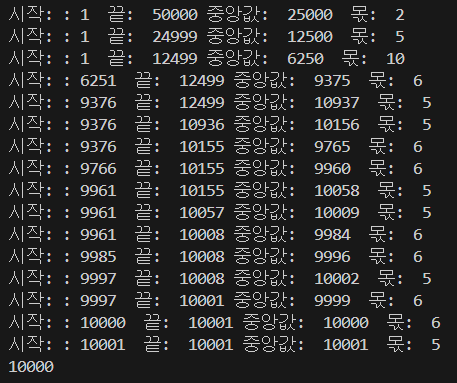
몫의 합이 K인 경우에도 사용할 수 있는 더 큰 랜선의 길이를 찾기 위해 오른쪽 범위에 대해서도 이분 탐색을 실시한다. 이를 반복문 및 재귀로 구현하면 다음과 같다.

반복문

k,n = map(int,input().split())
arr = [int(input()) for _ in range(k)]

start, end = 1, max(arr)
while start <= end:
    mid = (start+end)//2
    cnt = 0
    for v in arr:
        if v >= mid:
            cnt += v//mid
    if cnt >=  n:
        start = mid + 1
    else: 
        end = mid - 1
print(end)

재귀

k,n = map(int,input().split())
arr = [int(input()) for _ in range(k)]
start, end = 1, max(arr)

def binarySearch(start,end,n):
    if start > end: return 0
    
    mid = (start+end)//2
    cnt = 0
    for v in arr:
        cnt += v//mid
    
    if cnt >= n:
        res = binarySearch(mid+1, end, n)
        if res == 0: return mid
        else: return res
    elif cnt < n:
        end = mid - 1
        return binarySearch(start,end,n)
    else:
        start = mid + 1
        return binarySearch(start,end,n)

print(binarySearch(start,end,n))