[Java] 백준 9527 1의 개수 세기

https://www.acmicpc.net/problem/9527

난이도

골드2

문제

두 자연수 A, B가 주어졌을 때, A ≤ x ≤ B를 만족하는 모든 x에 대해 x를 이진수로 표현했을 때 1의 개수의 합을 구하는 프로그램을 작성하시오.

즉, f(x) = x를 이진수로 표현 했을 때 1의 개수라고 정의하고, 아래 식의 결과를 구하자.

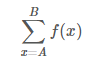
입력

첫 줄에 두 자연수 A, B가 주어진다. (1 ≤ A ≤ B ≤ 1016)

출력

1의 개수를 세어 출력한다.

내 코드

import java.util.*;
import java.io.*;

class Main {
    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        long start = Long.parseLong(st.nextToken());
        long end = Long.parseLong(st.nextToken());

        System.out.println(count(end) - count(start - 1));
    }

    static long count(long n) {
        if (n == 0) return 0;

        long count = 0;
        long powerOfTwo = 1;

        while (powerOfTwo <= n) {
            long totalPairs = (n + 1) / (powerOfTwo * 2); // 1이 반복되는 패턴 수
            long remainder = (n + 1) % (powerOfTwo * 2); // 나머지 부분에서 추가로 등장하는 1

            count += totalPairs * powerOfTwo; // 반복된 패턴에서 등장하는 1의 개수
            count += Math.max(0, remainder - powerOfTwo); // 남은 부분에서 추가되는 1

            powerOfTwo *= 2; // 다음 비트 자리수로 이동
        }

        return count;
    }
}

0  = 0000
1  = 0001
2  = 0010
3  = 0011
4  = 0100
5  = 0101
6  = 0110
7  = 0111
8  = 1000
9  = 1001
10 = 1010
11 = 1011
12 = 1100
13 = 1101
14 = 1110
15 = 1111

0~15까지의 숫자를 보면 각 자리(2^k)마다 1의 개수가 일정한 패턴을 보인다.
가장 오른쪽 비트(2^0)는 2번마다 한 번씩 1이 등장하고,
두 번째 자리(2^1)는 4번마다 두 번씩 1이 등장한다.

이 규칙을 활용해 '1' 개수를 빠르게 계산 가능하다고 한다.

2^k 자리수에서 1의 개수는
(n + 1) / (2 * powerOfTwo) * powerOfTwo
(n + 1) % (2 * powerOfTwo)에서 powerOfTwo를 초과하는 부분만큼 추가한다.