고정소수점이란?

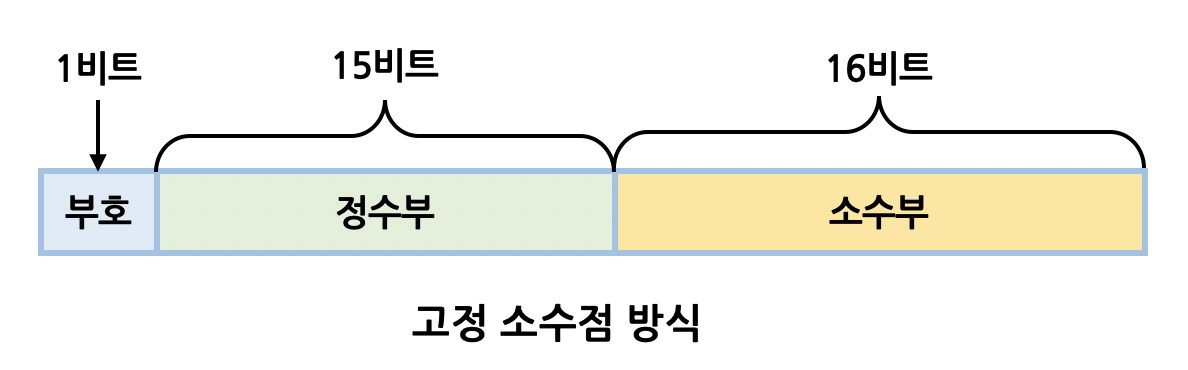
정수를 표현하는 비트수와 소수를 표현하는 비트수를 미리 정해놓고 해당 비트만큼만 사용해서 숫자를 표현하는 방식이다. 저는 이론을 이해하고 학습하는 것보다 바로 실전을 통해 이론을 학습하는 편이라서 먼저 예시를 통해 빠르게 알아보겠습니다. 예시를 들기위해 임의의 숫자인 263.3을 선택하였고 32비트를 사용하여 부호, 정수부, 소수부를 표현해보겠습니다.

부호의 경우 1비트를 차지하며 양수의 경우에는 0을, 음수의 경우에는 1로 표현합니다.

다음으로 263.3의 정수부를 구하는 과정을 가져보겠습니다.
2진수이기에 2로 나눠주면 다음 과정에서는 몫을 가지고 계속 실행시켜줍니다.

263 % 2 = 1
131 % 2 = 1
65 % 2 = 1
32 % 2 = 0
16 % 2 = 0
8 % 2 = 0
4 % 2 = 0
2 % 2 = 0
1 % 2 = 1

아래에서 위로 올라가면 읽어줍니다
100000111(2) -> 9비트
15비트 - 9비트 = 6비트
6비트를 모두 0으로 채워 정수부를 만들어 주면 000000+100000111 = 000000100000111(2) 이게 정수부입니다.

다음으로 소수부를 구해보는 과정을 해보겠습니다.

0.3 * 2 | 0.6 | 0
0.6 * 2 | 1.2 | 1
0.2 * 2 | 0.4 | 0
0.4 * 2 | 0.8 | 0
0.8 * 2 | 1.6 | 1
0.6 * 2 | 1.2 | 1
0.2 * 2 | 0.4 | 0
0.4 * 2 | 0.8 | 0
		.
		.
		.

0(1001)(1001)(1001)...
처음에 0뒤로는 계속 1001이 반복되는 과정을 거치지만 소수부의 비트는 최대 16비트이므로 16비트만 사용해줍니다.0100110011001100(2)으로 표현할 수 있습니다.

위 결과를 토대로 263.3을 고정소수점으로 나타내면 (0)(000000100000111)(0100110011001100)입니다.

하지만 고정소수점에는 단점이 존재합니다. 정수부의 bit를 늘려 큰 숫자를 표현할 수 있지만 정밀한 숫자를 표현하기 힘들고, 반대로 소수부의 bit를 늘려 정밀한 숫자를 표현할 수 있지만 큰 숫자를 표현하기 힘들다는 단점이 존재합니다. 이를 보완하기 위해서 부동소수점이 나왔습니다.

부동소수점이란?

부동은 영어로 float, 뜻은 떠다니다,유동적인이라는 의미를 나타내고 있습니다.
이는 소수점이 고정되어 있지 않고 좌우로 움직일 수 있다는 뜻입니다.

소수점이 자유롭게 움직인 다는 것은 표현할 수 있는 수의 범위가 매우 넓어진다는 장점을 가지고 있습니다.
바로 263.3을 부동소수점으로 구하는 과정을 구해보자.

고정소수점에서 구한 263.3의 정수부는 100000111(2), 소수부는 0100110011001100였다.
합치면 100000111.0100110011001100이다. 하지만 부동소수점에서는 지수부와 가수부를 사용하기때문에 표준 표기법으로 바꿔준다면 1.000001110100110011001100 * 2^8이 된다.
지수부인 8을 이진법으로 나타내면 100(2)으로 표현할 수 있다. 하지만 여기서 한가지 중요한 것이 있는데 바로 지수부는 양수와 음수를 둘 다 표현하기 위해서 8비트로 표현할 수 있는 숫자 영역을 반으로 나누어 양수와 음수를 표현하는 한다는 점이다.

00000000 ~ 01111110  => -127부터 -1까지인 음수를 표현
01111110 => 0을 표현
10000000 ~ 11111111 => 1부터 128까지를 표현

따라서 8을 표현하기위해서는 00001000에 127(01111111)을 더해야한다.
00001000 + 01111111 => 10000111이 바로 지수부이다.

다시 역으로 정리하면 0 10000111 000001110100110011001100에서 가수부는 000001110100110011001100이니 맨앞에 1하고 소수점을 추가한 1.000001110100110011001100이고
지수부는 8이니 가수부에 적용시키면 100000111.0100110011001100이다.
이를 10진수로 표현하면 263.3이 되는것이다.