[백준] 15685번: 드래곤 커브 문제 풀이

문제 링크

https://www.acmicpc.net/problem/15685

접근 과정

지문을 여러번 읽어야 겨우 이해가 되는 문제였던 것 같다.
0세대에서 1개
1세대에서 1개
2세대에서 2개
3세대에서 4개의 선분이 그려진다.

그리고

왼쪽 방향을 0
위쪽 방향을 1
오른쪽 방향을 2
아랫쪽 방향을 3이라고 했을 때,

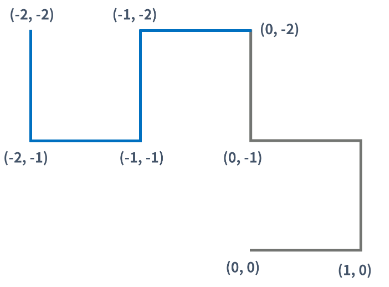
다음과 같은 예시에서 방향의 패턴을 직접 세보았다.

0세대: 0
1세대: 1
2세대: (2, 1)
3세대: (2, 3, 2, 1)

여기서 한가지 패턴을 발견하였는데,
n 세대는 역대 n세대들의 패턴의 역순에서 +1을 더한 것

다시 말해 1세대는 0세대의 0에서 +1이 된 것이고

2세대는 0~1세대의 (0, 1)을 뒤집어서 (1, 0)으로 만들고 각각 1씩 더해 (2, 1)로 만든 것과 같았다.

마지막으로 3세대는 0~2세대까지의 (0, 1, 2, 1)을 뒤집어서 (1, 2, 1, 0)으로 만들고, 각각 1씩 더해 (2, 3, 2, 1)로 만든것과 같았다.

이렇게 0~3세대까지의 전체 패턴은
(0, 1, 2, 1, 2, 3, 2, 1)이 됨을 알 수 있었다.

패턴 리스트 생성

이렇게 리스트에 값을 추가하는 과정을 메서드로 표현하면 다음과 같다.

static void draw_curve(int g) {
	list.add(d); // 처음 0세대 패턴 추가
	for (int i = 0; i < g; i++) {
    // 목표 세대가 될 때까지 반복
		int len = list.size();
        // 현재 시점의 리스트의 길이 저장
		for (int j = len - 1; j >= 0; j--) {
        // 현재 리스트의 역순으로, 
        //각 값에 방향을 변경하여 리스트에 추가
			int n = list.get(j);
			list.add((n + 1) % 4);
		}
	}
}

드래곤 커브 그리기

이렇게 생성된 패턴의 리스트 요소만큼 반복해서
현재 좌표에서 각 요소가 나타내는 방향으로 이동하면서 해당 위치에 표식을 남긴다.
메서드로 표현하면 다음과 같다.

arr[y][x] = 1; // 시작 위치에 표식 남기기
for (int dir : list) { // 패턴 리스트의 요소만큼 반복
	x += dx[dir]; // 각 요소가 가리키는 방향으로 좌표 이동
	y += dy[dir];
	arr[y][x] = 1; // 이동한 방향에 표식 남기기
}

정사각형 갯수 검사

마지막으로 101 x 101 배열의 요소를 모두 검사하면서
1 x 1 크기의 정사각형이 되는지를 확인한다.

int ans = 0;
for (int i = 1; i <= 100; i++) {
	for (int j = 1; j <= 100; j++) {
		if (arr[i][j] == 1 && arr[i - 1][j] == 1 && arr[i][j - 1] == 1 && arr[i - 1][j - 1] == 1)
			ans++;
		}
}

마지막은 브루트 포스이기 때문에 101x101 배열을 모두 검사하는게 1초로 충분할까 생각도 들었지만, 차피 nxn이 아닌 101x101 이기 때문에 크게 시간에 무리가 가지 않은 것 같다.

전체 코드

import java.io.*;
import java.util.*;

public class Main {
	static int d;
	static final int [] dy = {0, -1, 0, 1};
	static final int [] dx = {1, 0, -1, 0};
	static int arr [][] = new int [101][101];
	static ArrayList<Integer> list;
	static void draw_curve(int g) {
		list.add(d);
		for (int i = 0; i < g; i++) {
			int len = list.size();
			for (int j = len - 1; j >= 0; j--) {
				int n = list.get(j);
				list.add((n + 1) % 4);
			}
		}
	}
	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int N = Integer.parseInt(br.readLine());
		for (int i = 0; i < N; i++) {
			list = new ArrayList<>();
			StringTokenizer st = new StringTokenizer(br.readLine());
			int x = Integer.parseInt(st.nextToken());
			int y = Integer.parseInt(st.nextToken());
			d = Integer.parseInt(st.nextToken());
			int g = Integer.parseInt(st.nextToken());
			draw_curve(g);
			arr[y][x] = 1;
			for (int dir : list) {
				x += dx[dir];
				y += dy[dir];
				arr[y][x] = 1;
			}
		}
		int ans = 0;
		for (int i = 1; i <= 100; i++) {
			for (int j = 1; j <= 100; j++) {
				if (arr[i][j] == 1 && arr[i - 1][j] == 1 && arr[i][j - 1] == 1 && arr[i - 1][j - 1] == 1)
					ans++;
			}
		}
		System.out.println(ans);
	}
}