[BaekJoon] #2178 미로탐색

문제이해

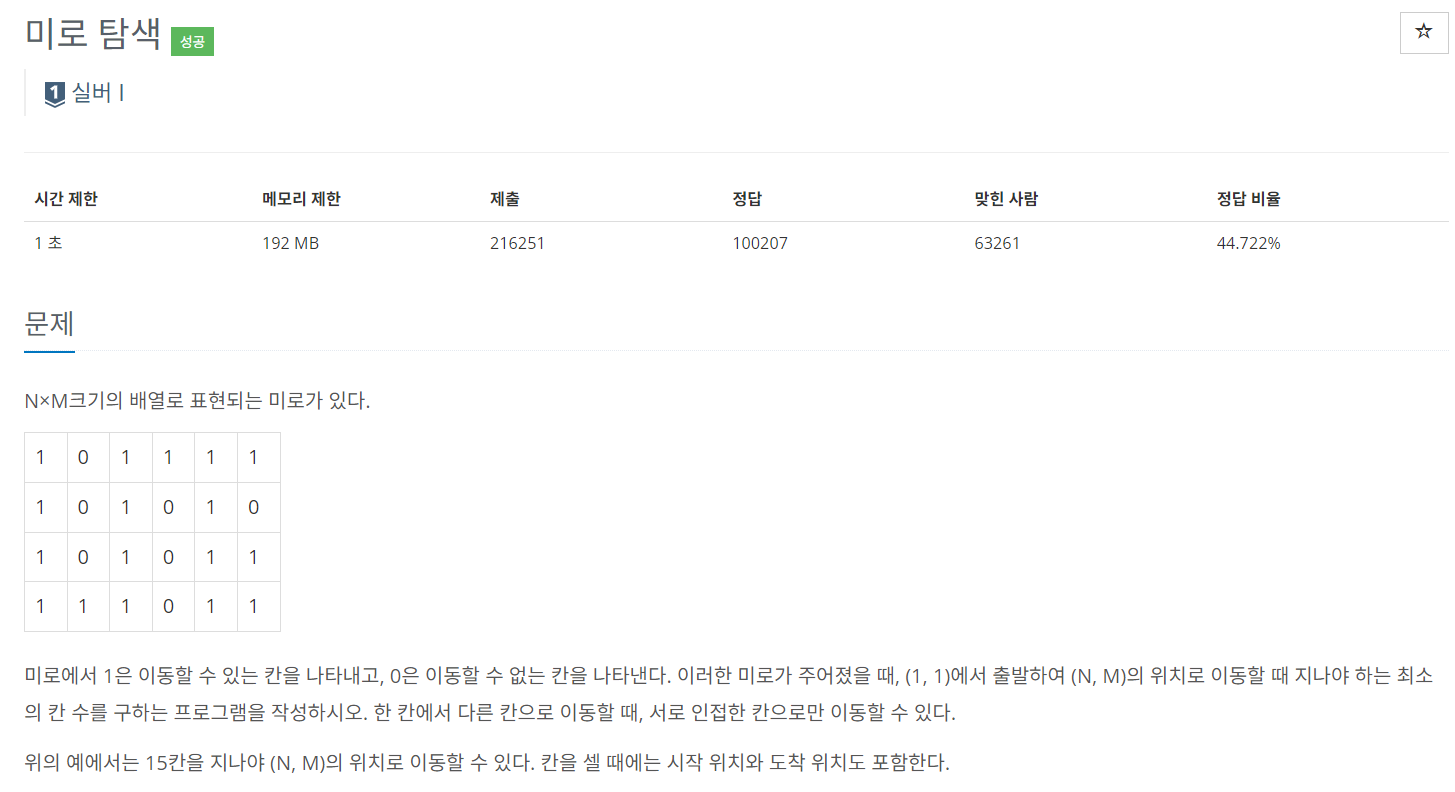
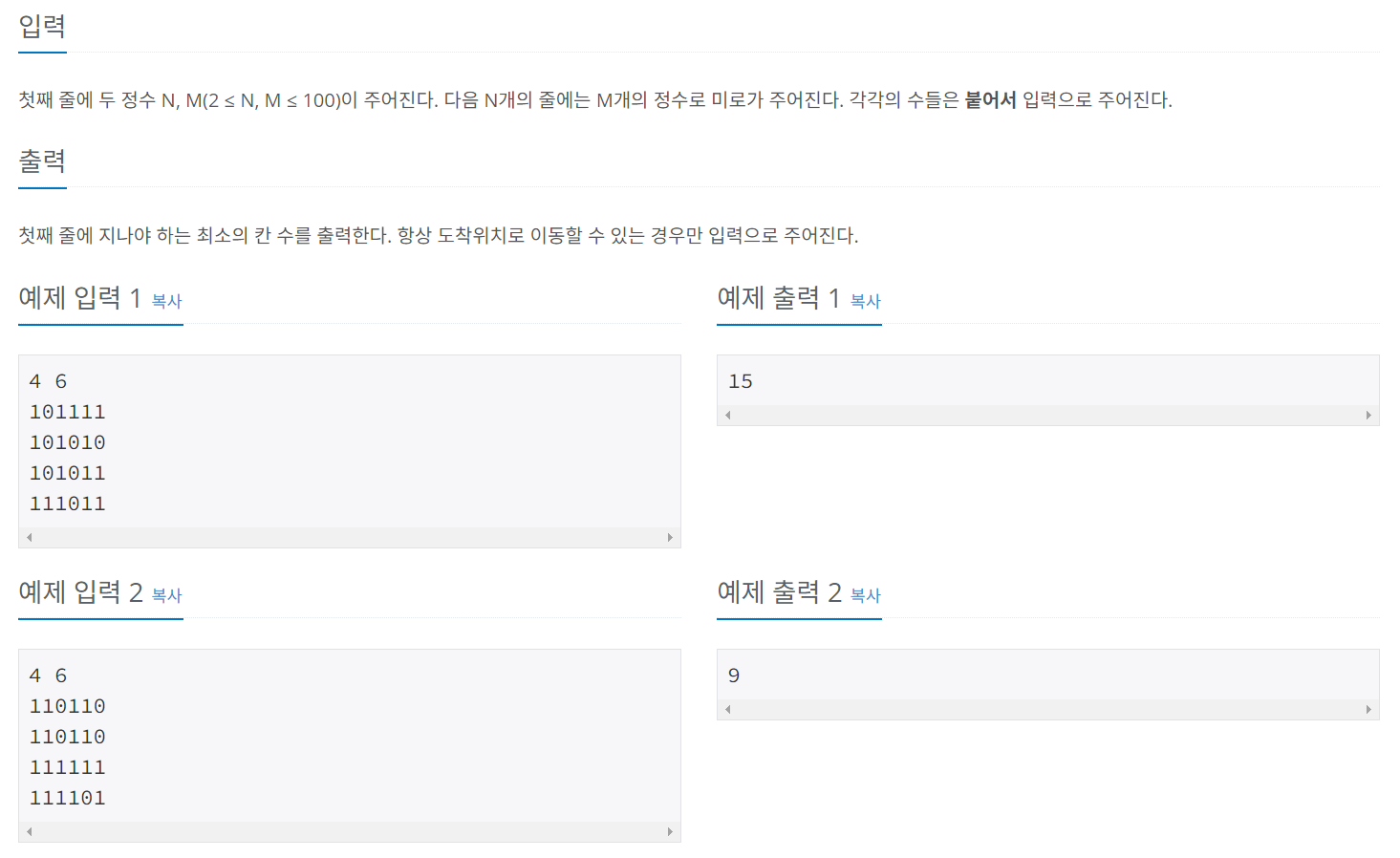
이 문제는 N*M 크기의 배열로 표현되는 미로가 주어지고, 미로의 (1,1) 위치에서 출발하여 (N,M)의 위치로 이동할때 지나야 하는 최소의 칸 수를 구하는 문제입니다.

문제접근

이 문제는 최단경로를 구하는 문제입니다.

최단경로를 구하기 위해 BFS를 이용해 문제를 풀어주었습니다.

BFS, DFS 를 이용해 인접한 원소를 순회하며 탐색한 노드의 개수를 세는 경우에 정수형의 count변수를 선언했었습니다.

이 방법은 단순 탐색 횟수를 기록하는것이지 최단거리를 보장하진 않습니다.

그러므로 최단경로를 구하기 위해서 최단 거리 배열을 선언해서 위치별 최소 칸수를 저장해주어야 합니다.

이것 외에는 보통의 BFS문제와 동일합니다.

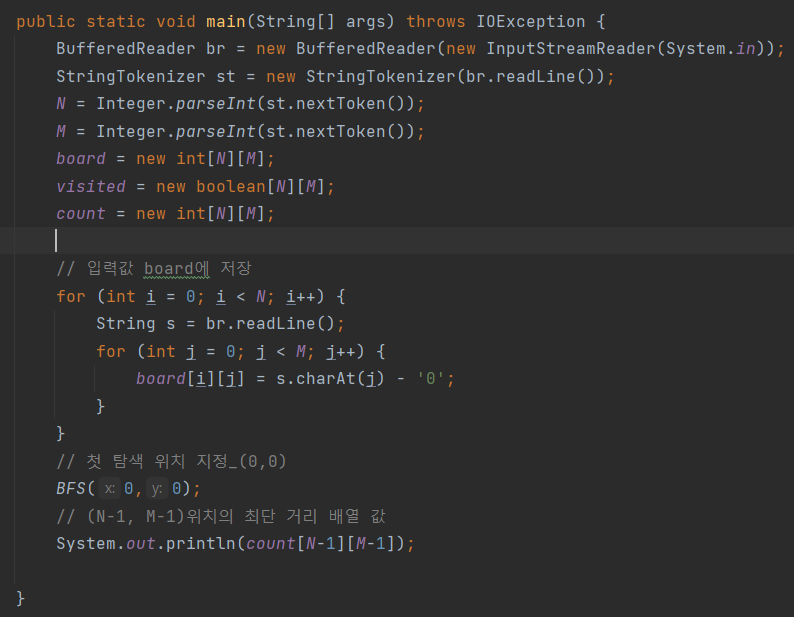
main

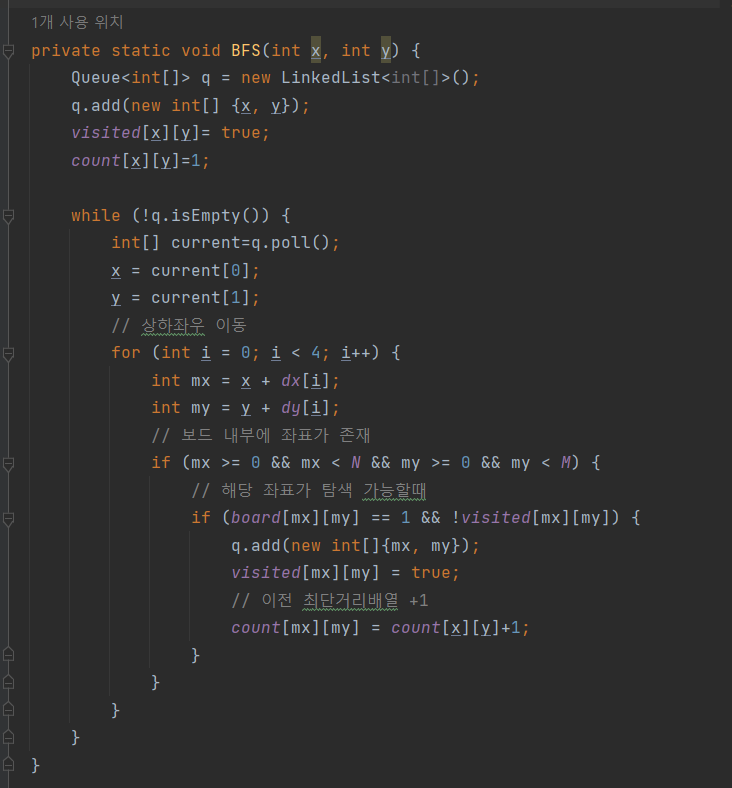
BFS

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;

public class Main {
    static boolean visited[][];
    static int board[][];


    static int[] dx = {-1, 1, 0, 0};
    static int[] dy = {0, 0, 1, -1};
    static int N, M;
    static int count[][];

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        N = Integer.parseInt(st.nextToken());
        M = Integer.parseInt(st.nextToken());
        board = new int[N][M];
        visited = new boolean[N][M];
        count = new int[N][M];

        for (int i = 0; i < N; i++) {
            String s = br.readLine();
            for (int j = 0; j < M; j++) {
                board[i][j] = s.charAt(j) - '0';
            }
        }
        BFS(0,0);
        System.out.println(count[N-1][M-1]);

    }

    private static void BFS(int x, int y) {
        Queue<int[]> q = new LinkedList<int[]>();
        q.add(new int[] {x, y});
        visited[x][y]= true;
        count[x][y]=1;

        while (!q.isEmpty()) {
            int[] current=q.poll();
            x = current[0];
            y = current[1];

            // 상하좌우 이동
            for (int i = 0; i < 4; i++) {
                int mx = x + dx[i];
                int my = y + dy[i];
                // 범위 내에 있고 이동 가능한 칸
                if (mx >= 0 && mx < N && my >= 0 && my < M) {
                    if (board[mx][my] == 1 && !visited[mx][my]) {
                        q.add(new int[]{mx, my});
                        visited[mx][my] = true;
                        count[mx][my] = count[x][y]+1;
                    }
                }
            }

        }
    }
}