탐색이란 많은 데이터 안에서 원하는 데이터를 찾는 과정을 의미합니다.
프로그래밍에서는 그래프나 트리 등의 자료구조 안에서 탐색을 하는 문제들을 자주 다룹니다.
트리는 그래프 중에서 싸이클이 존재하지 않는 특별한 형태의 연결그래프입니다.
트리에서 각 정점은 한개의 부모를 가지며, 모든 정점들이 연결되어 있습니다.
그래프는 트리와 다르게 싸이클을 가질 수 있으며, 간선이 양방향 또는 단방향일 수 있습니다.
이러한 그래프나 트리등의 자료구조에서 탐색을 하는 데에 이용하는 대표적인 탐색 알고리즘에는 BFS와 DFS가 있습니다.
Graph search
Graph search 의 목표는 가 주어졌을때 목표는 모든 정점과 간선을 탐색하는 것 입니다.
그래프의 정점과 간선을 탐색하면서, 그래프에서 발견된 연결된 정점들로 탐색트리나 스패닝 트리를 구성할 수 있습니다.
Graph search 를 할때 큐를 사용하며 너비 우선으로 정점들을 탐색하는 BFS와 스택을 사용하며 깊이 우선으로 정점을 탐색하는 DFS가 있습니다.
DFS알고리즘을 이용하는 중에 백트래킹이라는 기법을 사용할 수 있습니다.
BackTracking
백트래킹은 해를 찾는 과정에서 잘못된 경로일 경우, 다시 돌아가며 다른 경로를 탐색하는 기법입니다.
말 그대로 해석하자면, Back Track = 되추적 을 의미합니다.
즉, 현재 상태에서 가능한 모든 경로를 따라 들어가 탐색하다 해당 노드가 유망하지 않을 경우 더이상 탐색을 진행하지 않고, 전단계로 돌아가는, 즉 왔던 길을 되짚어 가는 backtrack 하는 기법 입니다.
백트래킹은 기법이고, DFS는 탐색 알고리즘입니다.
그러므로 백트래킹 기법은 여러 탐색 알고리즘이나 최적화 알고리즘에서 활용되고 그 중 하나가 DFS입니다.
어떠한 문제를 해결하는데에 있어 DFS기법으로 탐색을 진행하다, 백트래킹 기법을 적용해서 불필요한 부분을 가지치기 하는 방식으로 탐색한다면 효율적인 탐색을 할 수 있습니다.
backTracking vs DFS
둘의 차이에 대해 설명해보겠습니다.
백트래킹은 불필요한 탐색을 하지 않기 때문에, 유망하지 않은 노드를 만난다면 더이상 탐색을 진행하지 않습니다.
DFS는 완전 탐색을 기본으로 하는 그래프 순회 기법으로, 모든 노드를 방문하는 것을 목표로 합니다.
따라서, DFS만 사용하면 모든 노드들을 탐색해야 하기 때문에 비효율적이므로, 문제를 해결하기 위해서 위에서 말 했듯 DFS와 BackTracking 기법을 혼용하여 사용합니다.
즉, 노드를 방문하여 탐색을 진행하다, 유망하지 않은 노드를 가지치기 한 이후 얻은 그래프에 대해서 다시 DFS 탐색을 하면서 불필요한 탐색을 줄여나답니다.
예를 들어, DFS를 이용하다 조건문 등을 걸어 답이 절대로 될 수 없는 부분을 가지치기하고, back track하여 남은 그래프에 대해 다시 DFS를 진행하게끔 구현할 수 있습니다.
promising and pruning
노드의 유망성을 판단하여, 해가 될 가능성이 있다면 유망하다(promising) 이라고 말 하며, 불필요한 탐색 부분을 제거하는 과정을 가지치기(pruning)라고 부릅니다.
이제 DFS에 대해 알에보겠습니다.
DFS (Debth First Search)
DFS는 깊이 우선 탐색이라고 부르며 그래프와 트리의 깊은 부분을 우선적으로 탐색하는 알고리즘 입니다.
BFS 는 최단 경로 탐색에 유용합니다. 무향그래프, 혹은 가중치가 없는 그래프에서 특정 정점으로부터 다른 정점까지의 최단경로를 찾는데 자주 사용됩니다.
DFS와 BFS 모두 완전 탐색 을 기본으로 하지만, 깊이 우선으로 탐색하느냐 너비우선으로 탐색하느냐의 차이를 가지고 있습니다.
DFS도 BFS처럼 색상으로 정점의 상태를 표시합니다.
- white : 아직 방문하지 않은 상태
- Gray : 탐색중인 상태
- Black : 탐색이 완료된 상태
DFS는 스택이나 재귀함수를 통해 구현할 수 있습니다.
spanning Tree
스패닝트리란 ?
그래프의 모든 정점이 연결되어있는 트리를 말합니다.
즉, V개의 정점은 반드시 V-1개의 간선으로 연결되어있어야 하며, 트리이기 때문에 사이클이 형성되면 안됩니다.
DFS 를 이용한다면 스패닝트리를 만들 수 있습니다.
즉, 그래프에서 DFS 탐색을 하고, 탐색에 사용되지 않은 간선을 지우면 스패닝 트리를 형성할 수 있습니다.
기존의 그래프와 스패닝 트리가 겹치는 부분을 Tree edge라고 말 하고, 나머지를 Cross Edge라고 말 합니다.
스패닝 트리를 만든다면 주어진 그래프에서 최소 간선을 사용하여 모든 정점을 연결할 수 있습니다.
스패닝 트리는 추후에 크루스칼 알고리즘 프림 알고리즘에서 쓰입니다.
DFS Pseudo code
DFS(G)
for each u ∈ V do
color[u] ← white
π[u] ← NIL
time ← 0
for each u ∈ V do
if color[u] = white then
DFS-VISIT(G, u)
DFS-VISIT(G, u)
color[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u] do
if color[v] = white then
π[v] ← u
DFS-VISIT(G, v)
color[u] ← black
f[u] ← time ← time + 1
DFS_ timestamp
DFS는 각 정점에 두개의 타임스탬프를 기록합니다.
: 정점 가 처음으로 발견되고 회색으로 바뀔 때의 시간
: 정점 에서 탐색이 완료되고 검정색으로 바뀔 때의 시간
DFS _Time complexity
-
모든 정점을 방문하여 흰색으로 초기화 해야 하기 때문에
DFS에 의 시간이 소요됩니다. -
DFS-VISIT는 각 정점에 대해 한번 호출되고, 각 간선을 한 번만 처리하기 때문에 시간이 소요됩니다.
따라서, 전체 시간복잡도는 입니다.
예시를 통해 알아보겠습니다.
아직 모든 정점을 방문하기 전이므로 흰색인것을 확인할 수 있습니다.
DFS를 정점 𝑥부터 시작합니다. 정점 𝑥를 방문하고 𝑥를 회색(gray)으로 칠합니다. 정점 𝑥는 현재 탐색 중입니다.
다음으로 정점 s를 방문합니다. s도 역시 회색으로 칠해집니다. DFS는 다음으로 s에서 방문할 수 있는 이웃정점을 찾습니다.
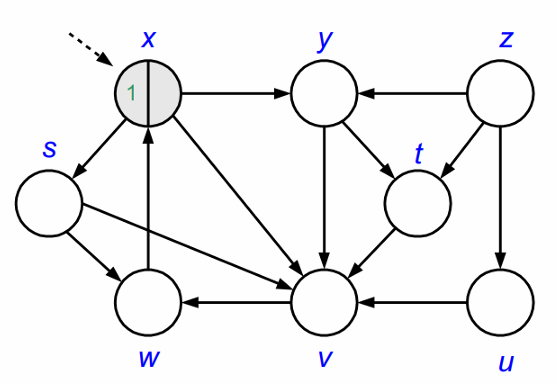
정점 s에서 간선을 따라가며 DFS는 계속해서 이웃한 정점을 탐색합니다.
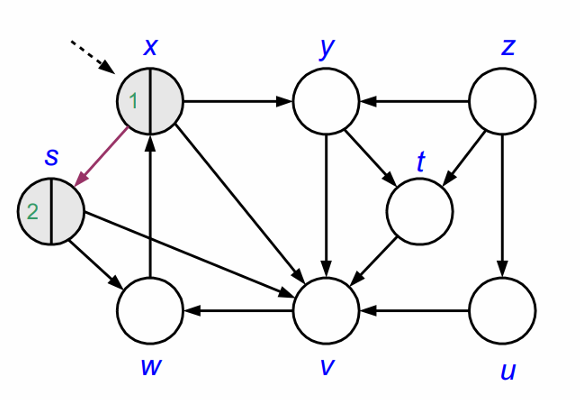
DFS는 정점 w를 방문하고 회색으로 칠합니다.
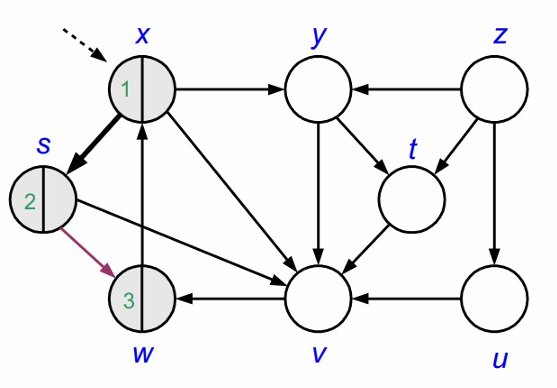
x는 이미 방문한 노드이므로 방문할 수 없습니다.
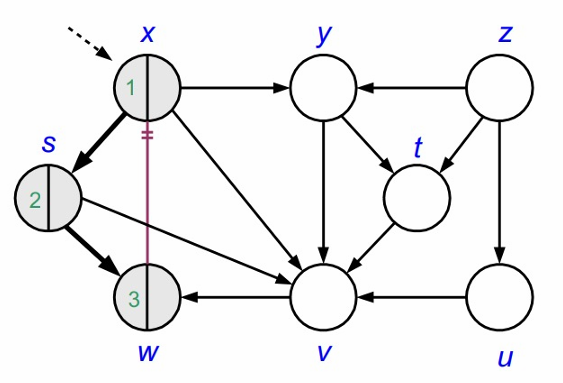
탐색이 완료되었으므로, 정점을 black으로 변경합니다.
이후, s의 인접정점 v의 색이 흰색이므로, v를 방문하고 회색으로 바꿉니다.
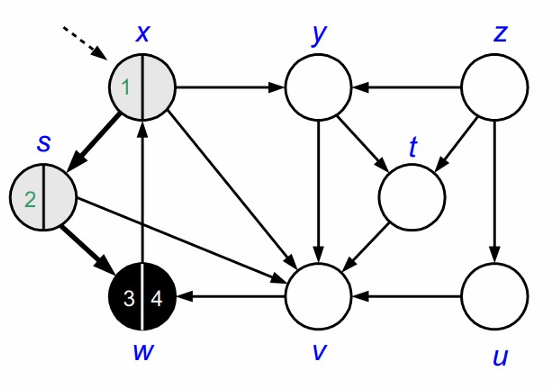
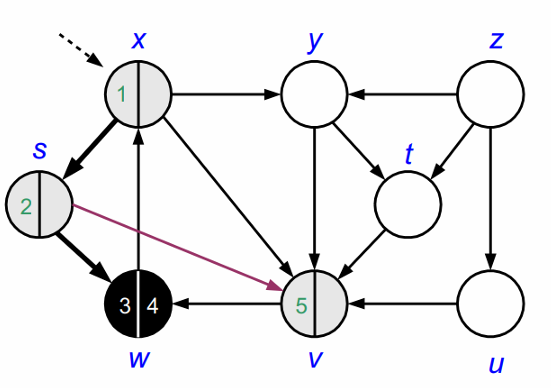
v의 인접정점인 W는 이미 방문한 정점이므로 방문하지 않습니다.
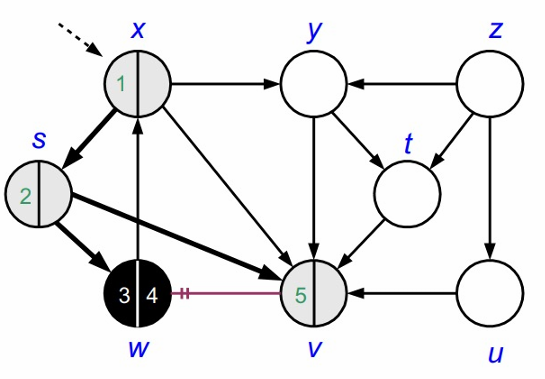
탐색을 완료했으므로, V의 색을 검정으로 바꿉니다.
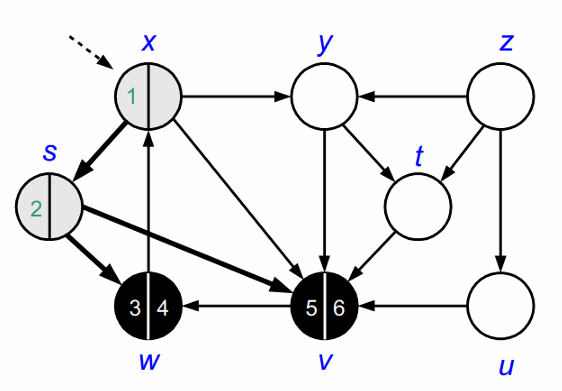
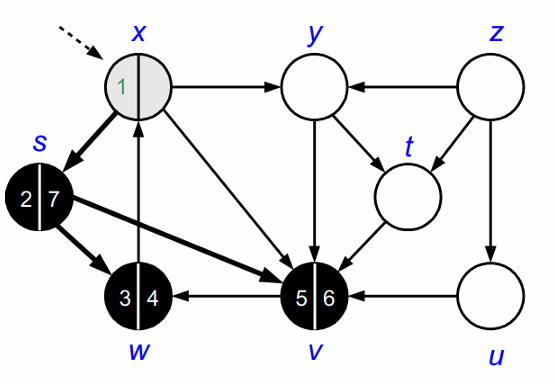
다시 x로 돌아가 인접정점인 y를 방문해 회색으로 바꿉니다.
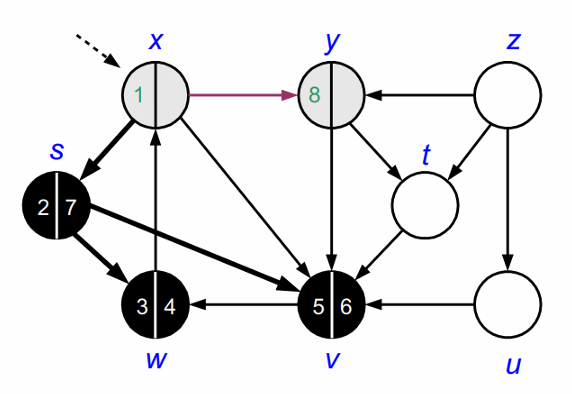
y의 인접정점인 v는 이미 방문했으므로 방문하지 않습니다.
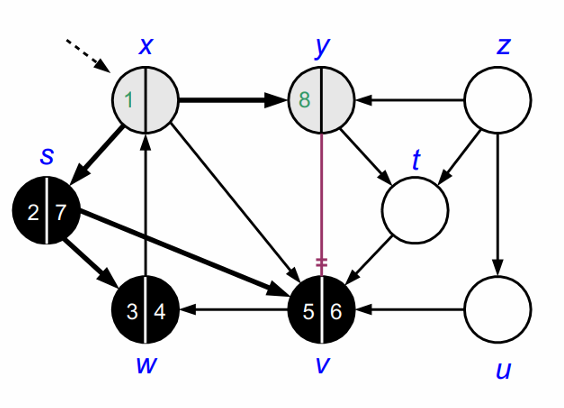
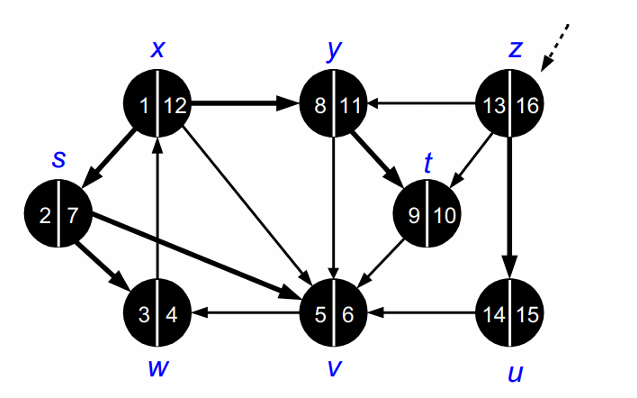
위의 과정을 모든 노드를 방문할 때 까지 반복합니다.
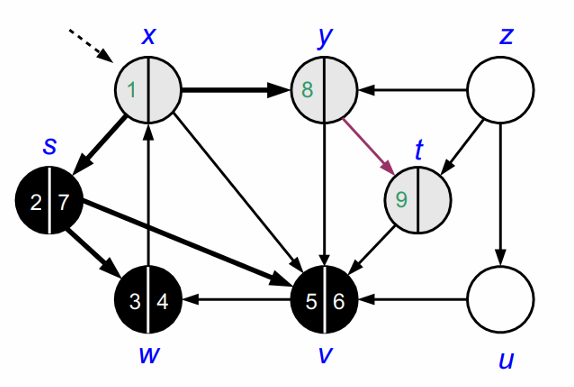
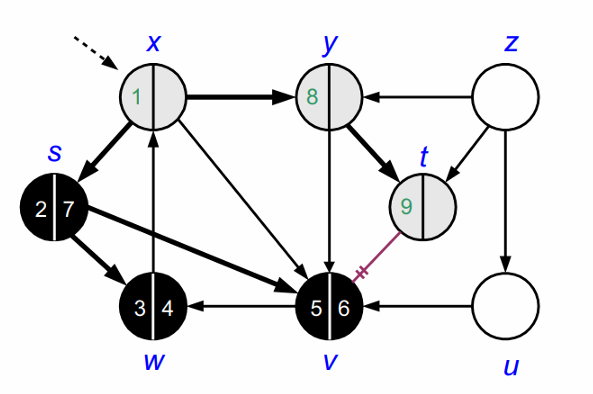
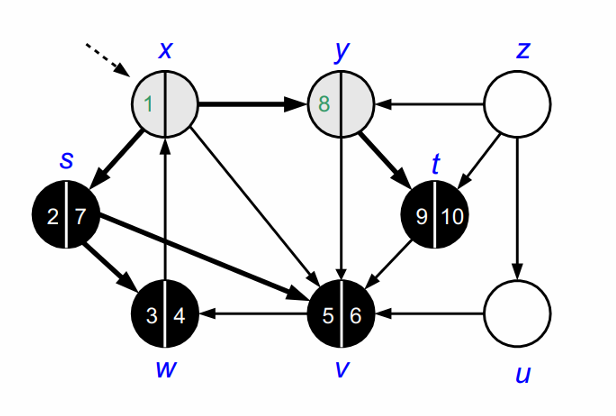
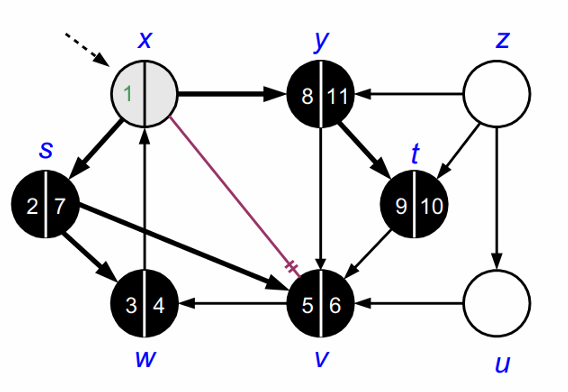
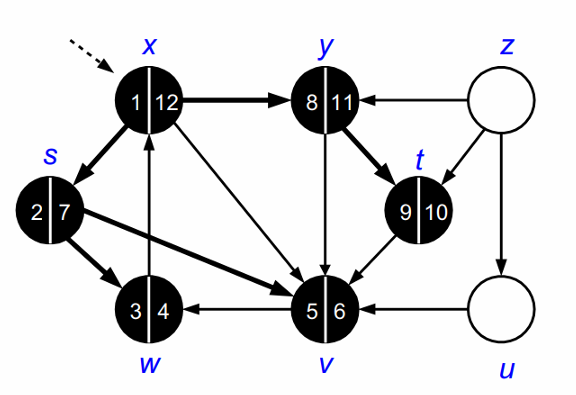
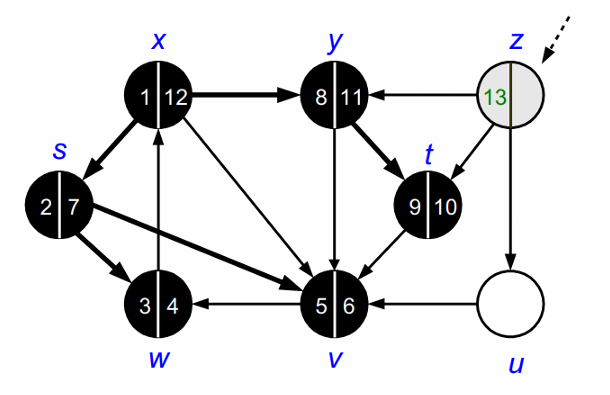
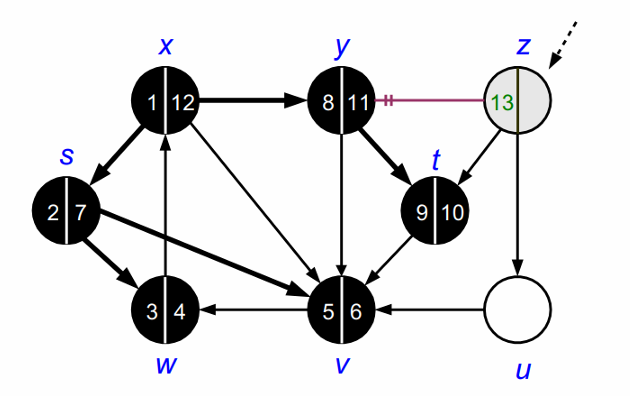
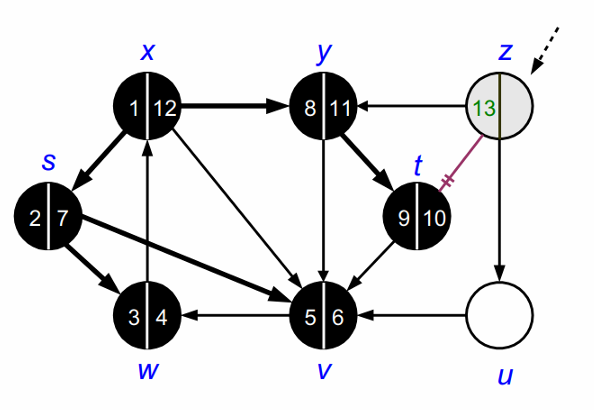
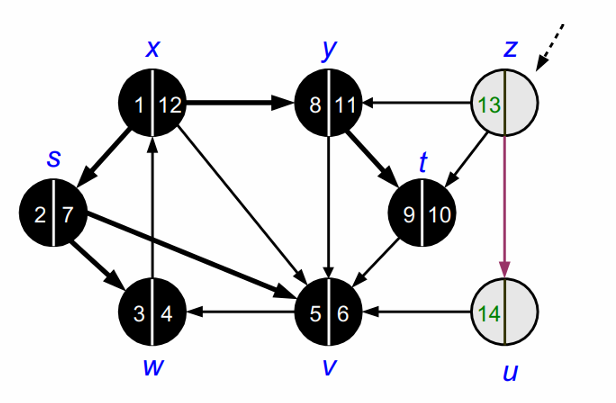
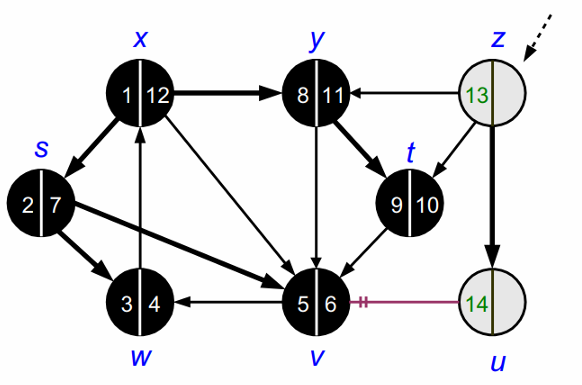
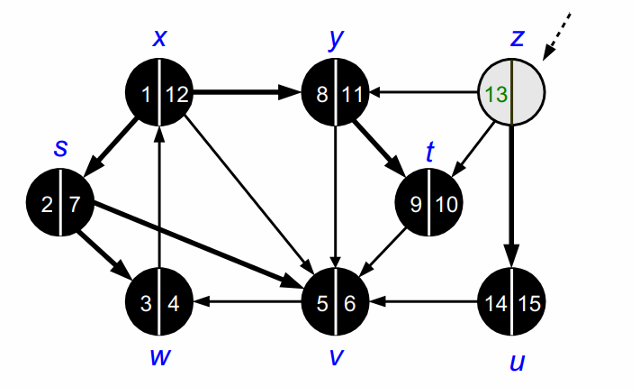
모든 노드를 방문하고 나면 DFS가 종료됩니다.
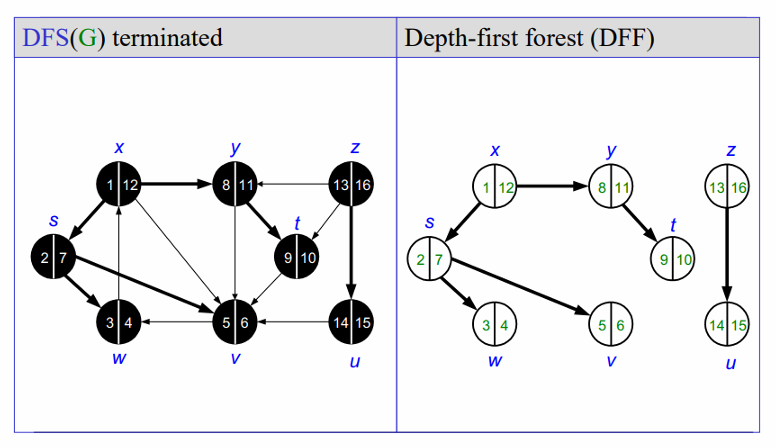
DFS가 종료되고 나면 다음과 같이 forest를 얻을 수 있습니다.
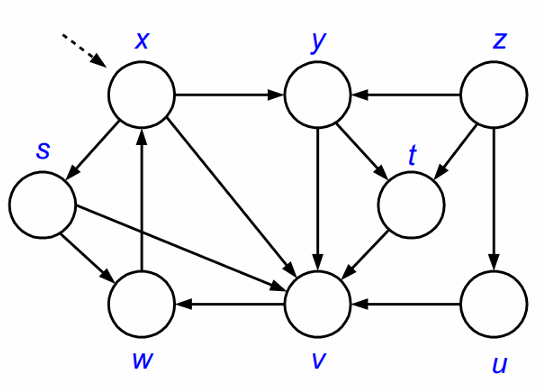
DFS: Parenthesis Theorem
각 정점 v는 발견시간 d[v]와 탐색 완료 시간 f[v]로 구간이 정의됩니다.
u와 v라는 두 정점에 대해서 다음 중 하나가 성립합니다.
- int [u] 와 int[v]는 완전히 분리되어 있습니다.
- int [v] 는 int[u]안에 완전히 포함되며, 이는 v가 u의 자손임을 의미합니다.
- int [u]는 int[v]안에 완전히 포함되며, 이는 u가v의 자손임을 의미합니다.
쉽게 말하자면 탐색 중에 회색 상태로 더 오랜 시간 유지된 정점일수록 트리의 상위 계층에 속합니다.
시작 정점으로부터 탐색을 진행하며 debth를 더해가며 탐색을 진행하다, 더 이상 탐색할 수 없을 때 노드를 black으로 칠합니다.
더 이상 방문할 자식 노드가 없을 때, 부모노드로 거슬러 올라와 다른 미탐색 노드를 탐색합니다.
그렇기 때문에, root에 가까울수록 아래의 subtree에 속한 노드들을 모두 탐색해야하므로 회색 상태로 오래 유지되고, 따라서 |f[v]-d[v]| 의 크기가 커집니다.
위의 설명을 그림과 표로 나타내면 아래와 같습니다.