본 포스팅은 Fastcampus 강의를 수강하며 일부 내용을 정리한 글임을 밝힙니다. 보다 자세한 내용은 아래 강의를 통해 확인해주세요.
참고 : Fastcampus 딥러닝을 활용한 추천시스템 구현 올인원 패키지 Online

---

Ch 06. Model-based Collaborative Filtering

---

📑 Paper Review

BPR: Bayesian Personalized Ranking from Implicit Feedback

UAI 2009 - Association for Uncertainty in Artificial Intelligence

• 특징 1. Matrix Factorization을 통해 Implicit Feedback 데이터 잘 활용 (implicit feedback 데이터를 이전에 잘 활용하기 어려웠는데, matrix factorziation을 통해 성능을 더욱 높일 수 있었음)

• 특징 2. BPR: 유저에 대해 아이템의 ranking을 매기는 문제

• Advanced Matrix Factorization

---

Abstract

• Implicit Feedback으로 추천 알고리즘 다루는 논문
• Matrix Factorization(MF)과 (adaptive) k-nearset-neighbor(kNN)으로 personalized ranking 실험
• Bayesian을 활용한 최적화 기법(BPR-Opt) 제시
• 위의 최적화 기법 적용하여 기존의 MF, kNN보다 더 우수한 성능 증명

Contribution

1. Maximum Posterior Estimator에 기반한 최적화 기법인 BPR-OPT 제안

2. BPR-OPT를 위한 LearnBPR 제안 ➡️ 기존 SGD보다 성능 우수

3. LearnBPR을 그 당시 최신 모델에 적용

4. BPR-OPT가 다른 방법보다 우수함을 실험적으로 증명

1&2. Introduction & Related Work

• 추천시스템 구현하기 위해 2가지 형태가 일반적 ➡️ Explicit과 Implicit 데이터

• 보통 Implicit 데이터가 더 많은 비중 차지하고, 더 어려운 문제

• Implicit 데이터로 user의 선호도 또는 취향 파악해야 함

• Implicit feedback으로 ranking을 추천할 수 있는 알고리즘 제시

  • 그냥 Implicit feedback으로 ranking을 했구나~ 생각할 수 있는데, 보통은 지금까지 평점을 정확히 예측(새 아이템에 대해 몇점을 주는지)하는 것에 focus했다면 이 방법은 implicit feedback 데이터 활용하여 특정 유저 입장에서 item i가 item j보다 더 선호하는지 ranking을 매기는 것에 초점

• 저자가 정의한 ranking을 추천하기 위한 optimization은 다음과 같다

  • item i와 j가 있을 때, user가 item i보다 item j를 더 선호한다 ➡️ $item$ $i$ $>$ $item$ $j$
  • 이때 학습할 파라미터를 최적화하는 것이 목적

3. Personalized Ranking

• Personalized Ranking

  • User에게 ranked list of items를 제안(또는 추천)하는 것

  • Item Recommendation 이라고도 부름

    • 추천알고리즘으로 예측한 결과 줄을 세워서 상위 아이템을 추천하는 방식이 아니라, 실제로 3점(예시)을 받았을 지도 모르는 아이템이 가장 ranking이 높기 때문에 그 아이템을 추천한다

• 본 논문은 Implicit Feedback으로 user의 취향 고려

  • Implicit Feedback은 주로 대부분이 positive feedback (단점)

    • User는 관심이 있든 없든 아이템을 살펴보기때문에 이것만으로는 negative라고 판단하기 어려움 (로그들을 남긴다는 것은 주로 positive라고 여겨짐)

  • Non-observed Item을 다루는 것이 중요한 포인트

  • Non-observed Item = real negative feedback + missing values

즉, Implicit Feedback을 사용하는 이유는 관측되지 않은 아이템을 다룸으로써 관측되지 않은 아이템이 실제로 negative한지 missing values(관심이 있는데 안 본 아이템)인지 분류해가면서 랭킹 매길 수 있기 때문

3.1 Formalization

• $U$: 모든 users의 집합, $I$: 모든 items의 집합
• 이때 각 user 별 personalized total ranking ($>_u ⊂ I^2$)을 구하는 것
  • ex) user i가 전체 아이템 100개에 대해 total ranking 매김
• $>_u$는 다음과 같은 특징을 가짐

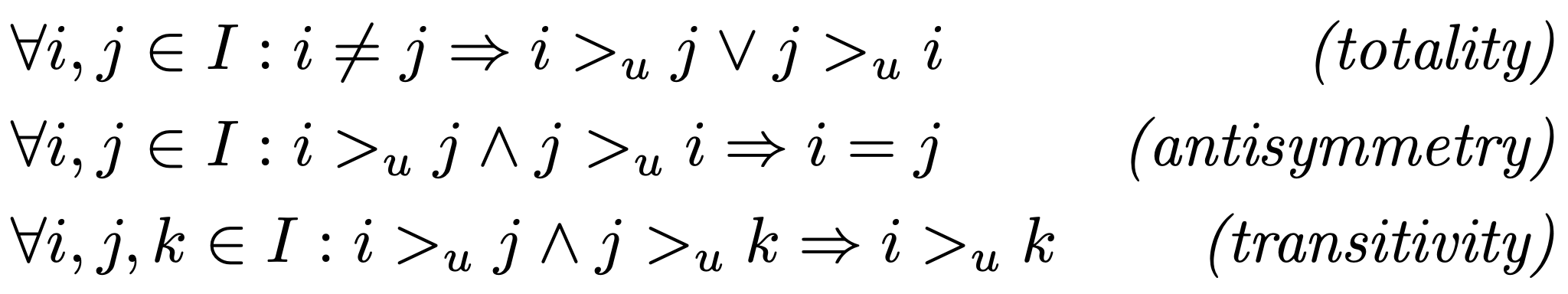
• totality: 아이템 i와 j가 다르면 i와 j의 순서가 있고, user u가 아이템 i를 더 선호할 수도 있고 아이템 j를 더 선호할 수도 있다는 것
• antisymmetry: user u가 아이템 i를 더 선호한다는 조건 + user u가 아이템 j를 더 선호한다는 조건 ➡️ 아이템 i=j
• transitivity: user u가 아이템 j보다 i를 더 선호하고, 아이템 k보다 아이템 j를 더 선호한다 ➡️ user u는 아이템 k보다 아이템 i를 더 선호한다

3.2 Analysis of Problem Setting (1)

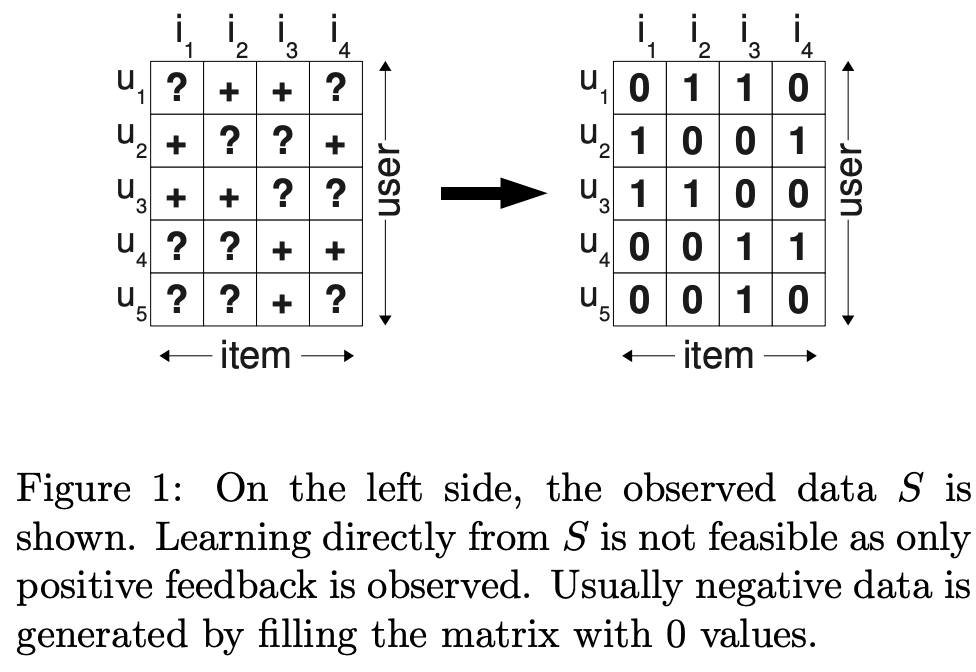
• 그림 1은 기존에 많이 사용하던 데이터 처리 방법

  • 각 user가 각 item에 대해 평가했을 때 ?인 missing values에 대해선 0으로 채움 (=선호하지 않는다)

• ?는 관측되지 않은 데이터, +는 관측된 데이터

• 0은 관측되지 않은 데이터 = 선호하지 않는 데이터(negative)

• 1은 관측된 데이터 = 선호하는 데이터(positive)

• Implicit data를 다루는 중요한 문제점이 있음

  • negative data에 대해 꼭 0으로 채워야 하느냐, 그럼 관측되지 않은 데이터도 0으로 채워야하느냐의 문제 셋팅

3.2 Analysis of Problem Setting (2)

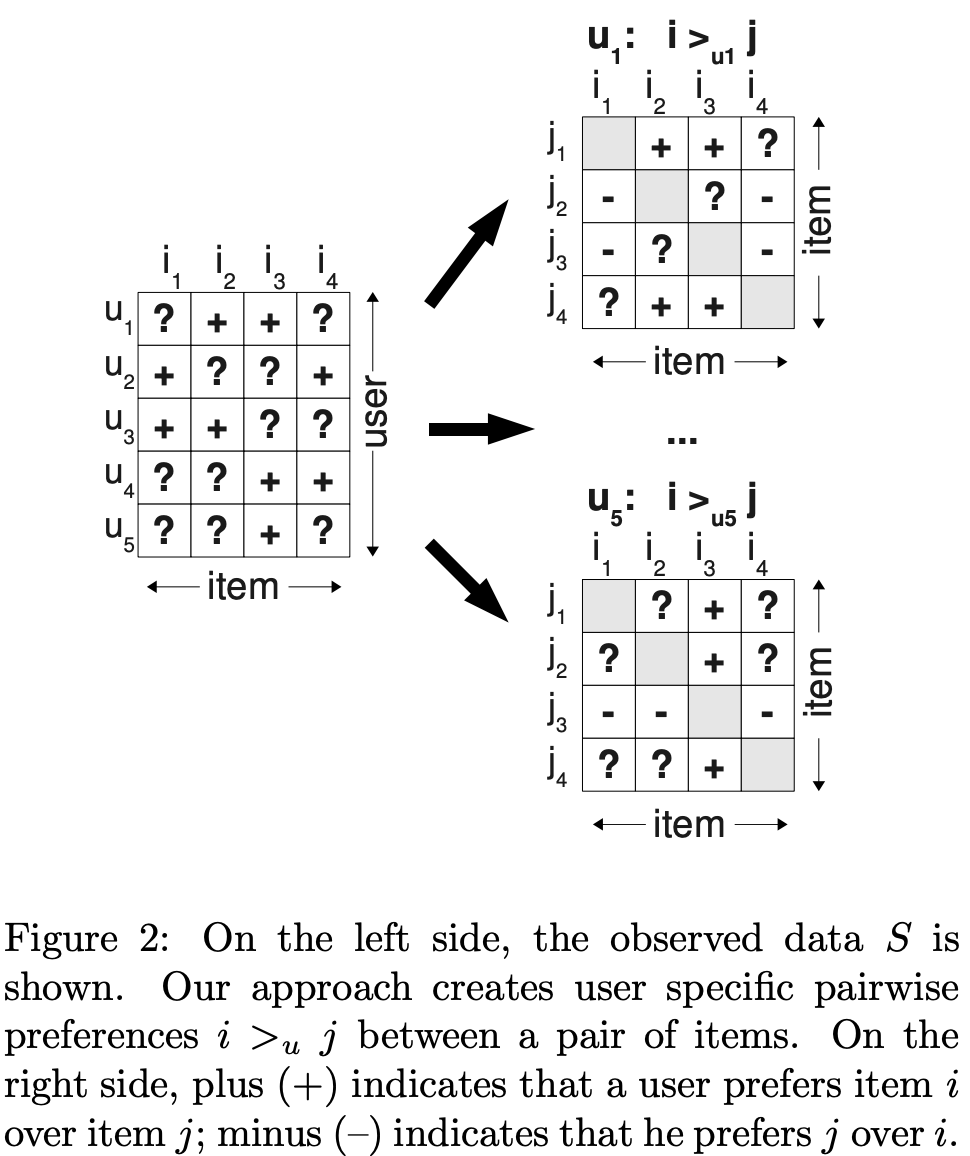
• 그림 2는 저자가 제안한 방법

• 전체 데이터를 pairwise preference ($i>_uj$)로 나타냄

  • 오른쪽 첫 번째 matrix 해석 예시
  • user 1이 아이템 i와 j에 대해 어떤 관계(선호도)를 가지는지 기존 user-item matrix를 통해 재구성
    • 즉, 하나의 matrix를 user 별로 쪼갠 것
  • 원본 matrix에서 user 1은 item 2, 3에 대해 positive feedback(+)을 준 상태
  • 오른쪽의 재구성된 matrix: item i2, i3은 평가를 받았기 때문에 평가를 받지 않은 item j1보다는 item i2, i3을 더 선호한다라는 뜻

• +: user가 item j에 비해 item i를 더 선호

• -: user가 item i에 비해 item j를 더 선호

• User가 보지 못한 item j에 비해 관측된 item i를 더 선호한다고 가정

• 유저가 (i, j) 모두 관측했거나, 관측하지 않았다면 어떤 선호도도 추론할 수 없음 (테스트셋으로 활용)

데이터셋 $D_s$

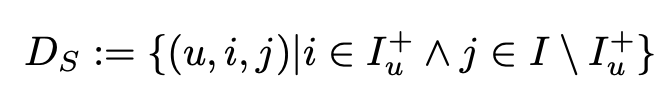
• $(u, i, j)$ : 어떤 유저인지, 어떤 아이템인지, 둘 중 어느 것을 더 선호하는지 tripple 형태의 데이터셋 구성 (중요한 포인트!)

  • i는 $I^+_u$에 속한 것, j는 $I^+_u$에 속하지 않은 나머지

• $(u, i, j)$의 의미: User u는 item j보다 item i를 더 선호한다는 것

• $>_u$는 antisymmetric이기 때문에 negative는 implicit이라고 가정

저자가 제안한 방법의 장점

• 학습셋 $D_s$는 positive, negative, missing value로 구성됨
• 아이템쌍 (i,j) (재구성된 user별 matrix에서)에서 관측되지 않은 결측값 ➡️ 테스트셋
• 학습셋과 테스트셋은 disjoint함
• 학습셋은 실제 랭킹 목적에 맞게 만들어짐
• 관측된 데이터의 부분집합인 $D_s$을 학습 데이터로 사용 ➡️ 이중 관측되지 않은 결측값들을 이용해 테스트셋 생성 후 평가

4. Bayesian Personalized Ranking (BPR)

• 주어진 학습 데이터 $D_s$로 Bayesian Personalized Ranking 구하는 방법 설명

• $p(i>_uj|θ)$에 대한 likelihood function과 model parameter $p(θ)$에 대한 prior probability를 사용한 베이지안 문제로 볼 수 있음

• 다음과 같은 순서로 section 구성

  • 4.1 BPR Optimization Criterion
    • 4.1.1 Analogies to AUC optimization
  • 4.2 BPR Learning Algorithm
  • 4.3 Learning models with BPR
    • 4.3.1 Matrix Factorzation
    • 4.3.2 Adaptive K-Nearsert Neighbor

4.1 BPR Optimization Criterion (1)

• 사후확률에 대한 수학적 표현 참고
  $P(posterior)∝likelihood\times P(prior)$

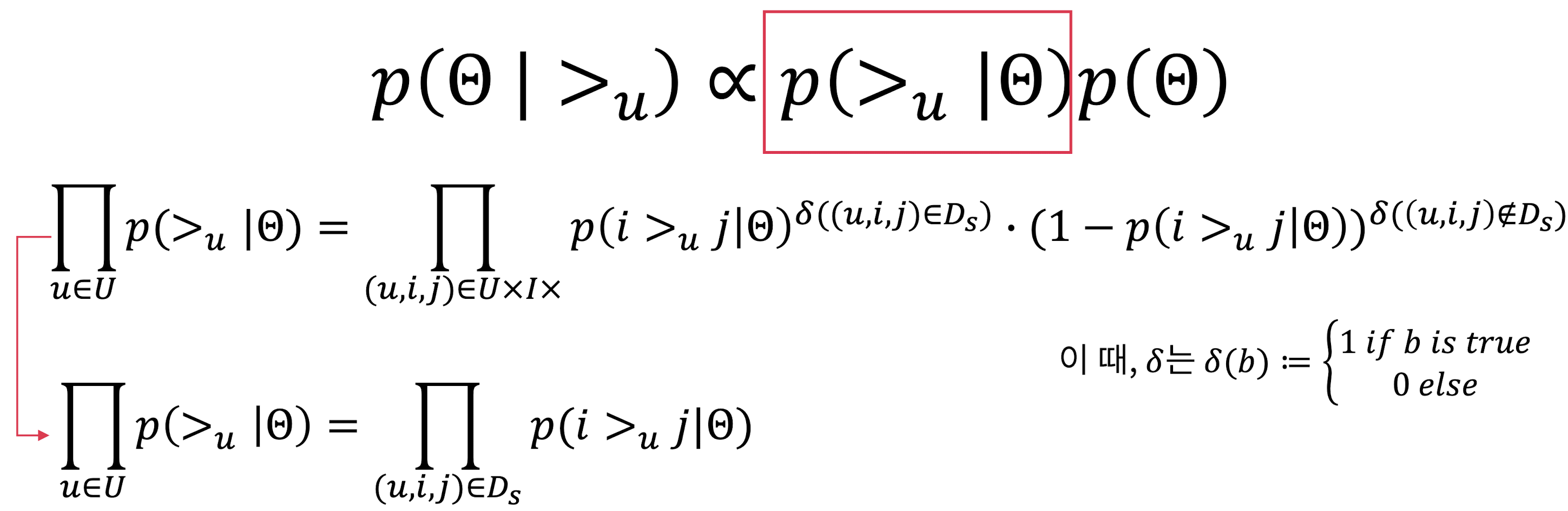
• 사후 확률 추정에 대한 likelihood와 prior에 대한 식
• 최종 목적은 $p(θ|>_u)$를 최대화 하는 모델 파라미터를 찾는 것
• 우변에 대한 복잡한 식은 Totality와 Antisymmetry에 따라 최종적으로 맨 아래 식으로 간단하게 정리 가능
  • 수학적 해석: user u가 아이템 i를 j보다 더 선호하는 모델 파라미터가 있을 때, 이때 확률을 값을 전부 곱해주는 것

4.1 BPR Optimization Criterion (2)

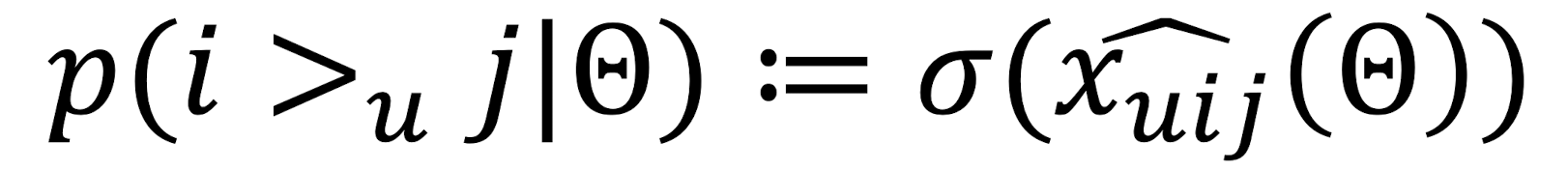
• $\hat{x_{uij}}(θ)$: user u와 item i,j의 관계를 나타내는 모델 파라미터 벡터의 실제 함수
  ➡️ 즉, $p(i>_uj|θ)$은 $\hat{x_{uij}}(θ)$를 추정하면서 u,i,j 사이의 관계를 모델링하는 것
• 전체 순서를 모델링하는 것이 이전 복잡한 식에 비해 비교적 간단해졌음

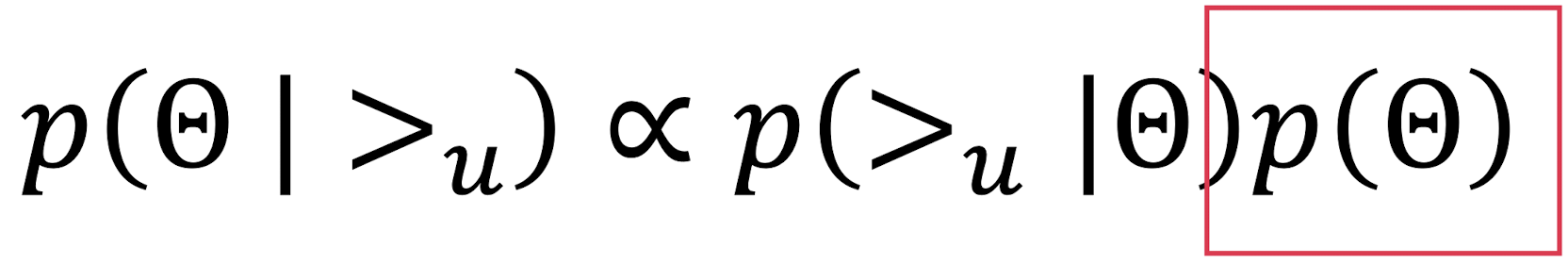
• $p(θ)$: 사전 확률분포, prior ➡️ $p(θ)$~$N(0,\sum_{θ})$로 나타내고 (정규분포를 따른다), $\sum_{θ}=λ_θI$로 정함
• Likelihood와 prior 모두 정의했으므로, posterior를 공식에 따라 구할 수 있음

4.1 BPR Optimization Criterion (3)

최종적으로 BPR-OPT는 posterior을 구하기 위해 likelihood와 prior로 나누어 다음과 같은 식이 도출됨 ➡️ 최종적으로 모델 파라미터를 최적화하는 과정의 중요한 포인트가 됨

4.2 BPR Learning Algorithm

• BPR Learning Algorithm은 $θ$를 계속해서 업데이트하는 과정

• 미분가능하기 때문에 gradinet descent로 optimizaiton함

  • 식에서 $θ$ + alpha 뒷 부분이 gradient

• SGD가 적절한 선택지가 아니기 때문에 LEARN-BPR 제안

  • Triples를 학습하는 Bootstrap 기반 Stochastic Gradient-Descent 알고리즘

• 랜덤하게 triples를 선택하는 SGD 알고리즘을 사용한다는 것

  • 이때 Bootstrap 기반 SGD 알고리즘 사용하는 이유는, 동일한 쌍의 데이터 선택할 확률이 적음
  • Implicit data에서 user u에 대한 item i, j의 triples data를 랜덤으로 뽑기 때문에 데이터 전수가 아닌 boostrap sampling만해도 데이터가 많기 때문에 충분함

4.3 Learning models with BPR

BPR을 활용해 어떻게 Matrix Factorization과 Adaptive k-NN에 적용할 수 있을까

Matrix Factorization

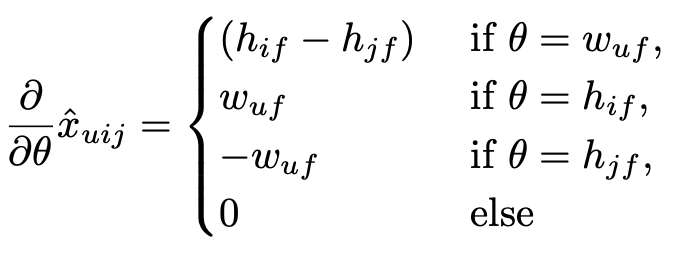
Adaptive K-Nearset Neighbor

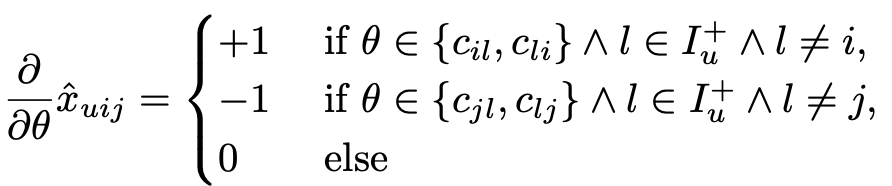
➡️ 사실상 gradient만 알면 모델 파라미터를 계속해서 업데이트 시킬 수 있기때문에 gradient를 어떻게 정의할 것인지가 중요, 즉 LearnBPR 최적화를 위해 모든 모델 파라미터 $θ$에 대한 $\hat{x_{uij}}$의 gradient만 알면 됨

추후에 논문 참고하여 BPR을 FM과 k-NN에 적용한 방법에 대해 더 자세히 살펴보기

6. Evaluation

• 저자는 Rossmann이라는 데이터셋과 Netflix 데이터셋을 활용하여 어떤 방법이 더 성능이 좋은지 비교
• BPR-MF, BPR-kNN (초록색)이 제일 성능이 좋음

7. Conclusion

• 사후확률을 최대화하는 베이지안에 의한 새로운 방법론 제시
• Personalized Ranking을 위한 optimization 기법인 BPR-OPT 제안
• LearnBPR: Bootstrap Sampling을 통한 Stochastic Gradient Descent를 사용하여 모델 파라미터 업데이트
• 기존 Matrix Factorization, k-Nearset Neighbor 모두 적용했으며 성능 또한 우수했음

---

More Information

• Code Reference: https://github.com/benfred/implicit
• VBPR: Visual Bayesian Personalized Ranking from Implicit Feedback
  • Visual: 옷, 영화 썸네일 등의 이미지 데이터를 활용
  • Runing He, Julian McAuley