Ch 08-4. Factorization Machine

Yeonghyeon·2022년 8월 10일

FM Factorization Machine 논문리뷰 딥러닝기반 추천시스템 추천시스템

Recommender System

목록 보기

23/33

본 포스팅은 Fastcampus 강의를 수강하며 일부 내용을 정리한 글임을 밝힙니다. 보다 자세한 내용은 아래 강의를 통해 확인해주세요.
참고 : Fastcampus 딥러닝을 활용한 추천시스템 구현 올인원 패키지 Online

Ch 08. Recommender System with Deep Learning

Matrix Factorization과는 다른 개념, 착각하지 말기!

📑 Paper Review

Factorization Machines

2010 IEEE International Coference on Data Mining

Factorization Machine 자체에서는 딥러닝을 다루진 않지만, 이후에 DeepFM 논문을 살펴보기 위해 다룰 필요 있음
간단한 user-item matrix에서 user와 item의 interaction을 학습하기 위한 중간의 latent factor를 찾아가는 과정 속에서 matrix factorization을 다뤄왔음
그런데 Factorization Machine은 딥러닝을 사용하진 않지만 딥러닝스럽게 feature를 만들고 다양하게 쓸 수 있는 장점이 있음

Abstract

Factorization Machine은 SVM(Support Vector Machine)과 Factorization Machine의 장점을 합친 모델
- SVM: 데이터가 있을 때 support vector들을 찾아서 이를 기준으로 데이터를 나누는 대표적인 머신러닝 알고리즘 (kernel 사용 등등)
- Factorization Machine 예시: Matrix Factorization, Parallel factor analysis, specialized model(SVD++, PITF or FPMC)
Real valued Feature Vector를 활용한 General Predictor이다
- 실수값들을 feature vector로 활용해서 gereral predictor를 만든다
- General Predictor: Factorization Machine은 classification, regression 등 다양하고 general 하게 풀 수 있는 알고리즘이다
Factorization Machine의 식은 linear time ➡️ 계산복잡도가 낮다
일반적인 추천시스템은 special input data, optimization algorithm 등이 필요하지만 반면, Factorization Machine은 어느 곳에서든 쉽게 적용 가능

Introduction

Factorization Machine은 general predictor이며, high sparsity에서도 reliable parameters 예측 가능
Sparse한 상황에서 SVM은 부적절
- cannot learn reliable parameters (‘hyperplanes’) in complex
  (non-linear) kernel spaces
FM은 복잡한 interaction도 모델링하고, factorized parametrization을 사용
Linear Complexity이며 linear number of parameters 이다

Contributions

Factorization Machine의 장점 3가지

(1) Sparse Data
(2) Linear Complexity
(3) General Predictor로써 추천시스템 이외 다른 머신러닝에서 사용 가능

Prediction Under Sparsity

movie 데이터를 다음과 같은 S 집합 형태로 만듦
- (user, item, time, rate)
- sparse한 상황에서도 다음과 같은 집합으로 데이터를 만들 수 있다는 것을 강조
일반적으로 볼 수 있는 영화 평점 데이터의 설명 (Sparse Data)
Matrix Factorizaiton은 user와 movie, 해당 rating만 사용
Factorization Machine은 더 다양하게 사용 가능
- time을 넣을 수 있는 방법에 대해 데이터화해서 (feature vector로 만들어서) 학습할 수 있다는 것이 아주 중요한 특징!

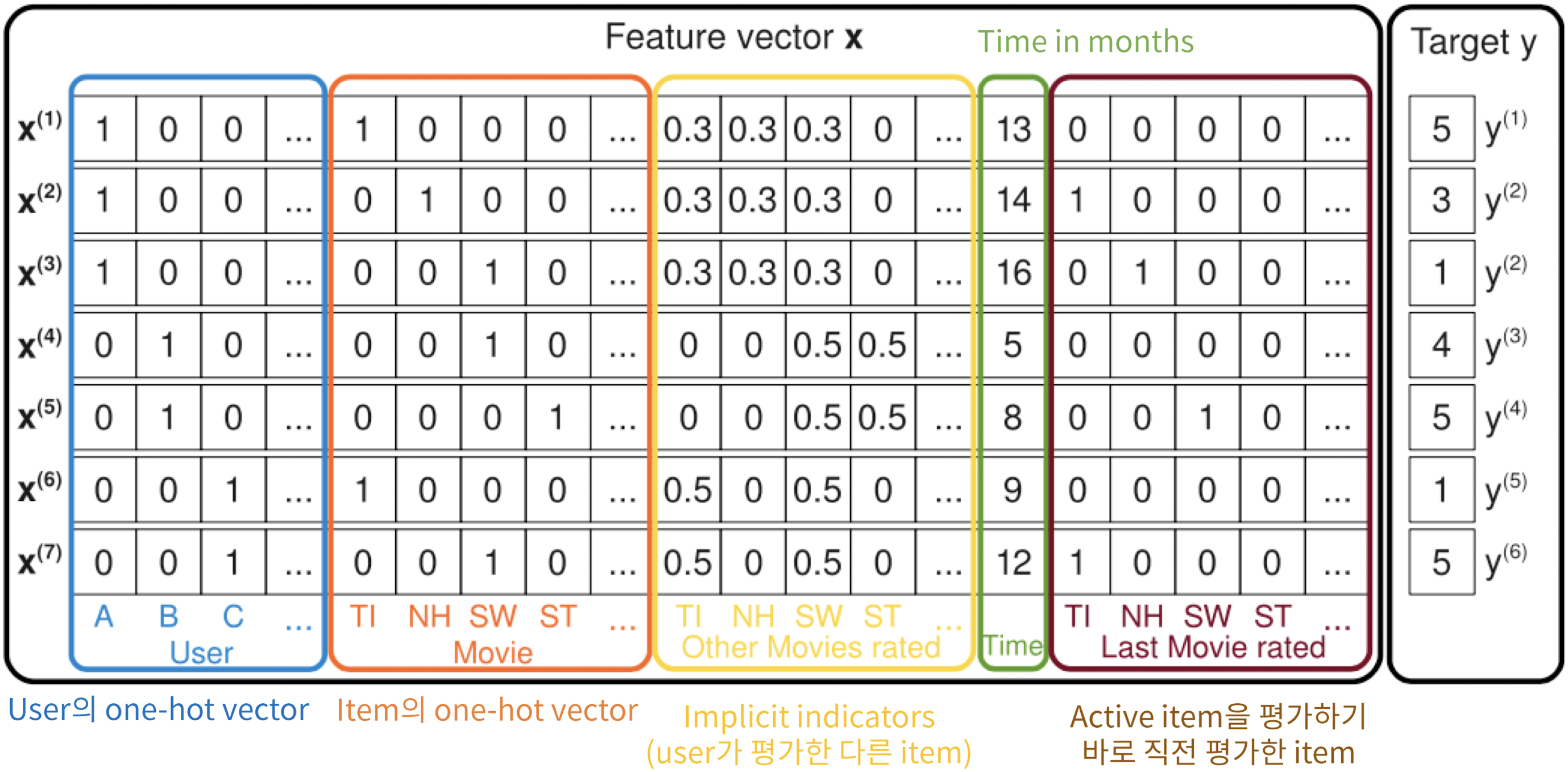
다음과 같이 Feature vector $x$ 를 만들어서 Factorization Machine을 만들어보겠다는 것
- Matrix Factorization의 경우, x축은 user, y축은 movie의 user-item matrix로 작업이 이루어졌음
- but FM의 경우, 하나의 feature x에 user, moview, implicit indicators(user가 평가한 다른 아이템 ➡️ 동일한 가중치 형태로 주어서 평가를 했구나를 표시), Time in months, Last Movie reated(one-hot vector 형식) 등 다양한 데이터가 구성되어 있음
- 해당 feature $X$ 를 가지고 있을 때 Target $y$ 가 존재
- Matrix Factorization과는 완전히 다른 접근이면서 SVM과는 비슷한 접근 (SVM에 feature를 그대로 넣어서도 학습 가능하겠지, but 성능 + 속도 차이가 존재할 것)

Factorization Machine (FM) - Model Equation (1)

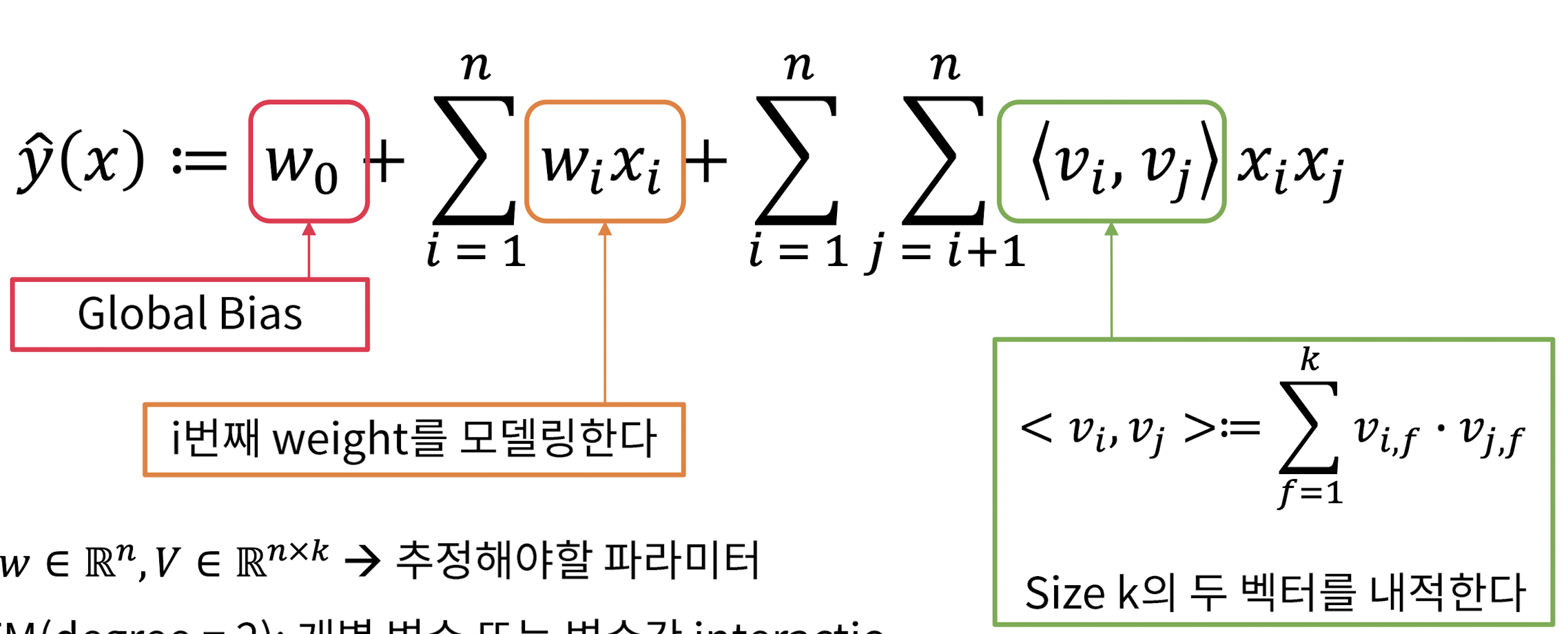
Size $k$ : 이게 바로 factorized parameters ➡️ 이 마지막 항이 matrix factorization 개념을 조금 추가한 것이라고 생각
- size k로 내적했기에 linear 연산이 된 것!
$w_0 \in \R$ , $w \in \R^n$ , $v \in \R^{n\times k}$ ➡️ 추정해야 할 파라미터
2-way FM(degree=2): 개별 변수 또는 변수간 interaction 모두 모델링
- 변수간 interaction을 잘 보기 위해 2-way인데, n-way도 가능함 (논문 뒷부분)
다항 회귀와 매우 흡사하지만, coefficient 대신 파라미터마다 embedding vector를 만들어서 내적

Factorization Machine (FM) - Model Equation (2)

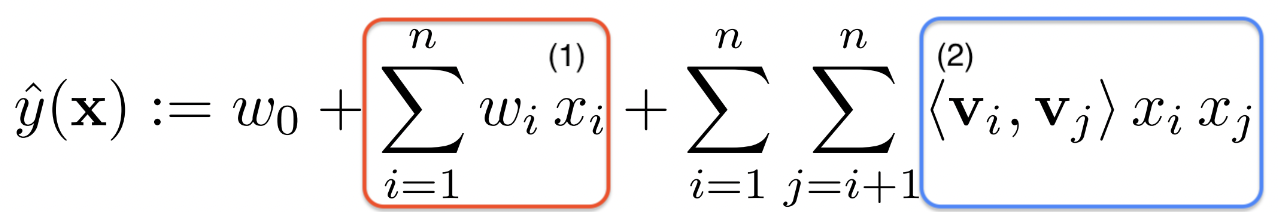
(1) 식

Matrix Factorization의 경우 ➡️ $w_u\times x_i$
- user와 item latent vector를 내적하면서 gradient를 업데이트 하는 방식
Factorization Machine ➡️ $w_i\times x_i$
- feature vector ( $x$ )만을 가지고 학습
- $x_i$ 마다 구함

(2)

변수간 latent vector 조합을 고려
이때 degree=2인 경우 모든 interaction을 얻을 수 있다
Pairwise feature interaction을 고려하기 때문에 sparse한 환경에 적합
- $<v_i,v_j>$ 가 변수간 interation을 구할 때 latent vector를 조합하기때문에 Pairwise feature interaction을 고려할 수 있다

Factorization Machine (FM) - Computation

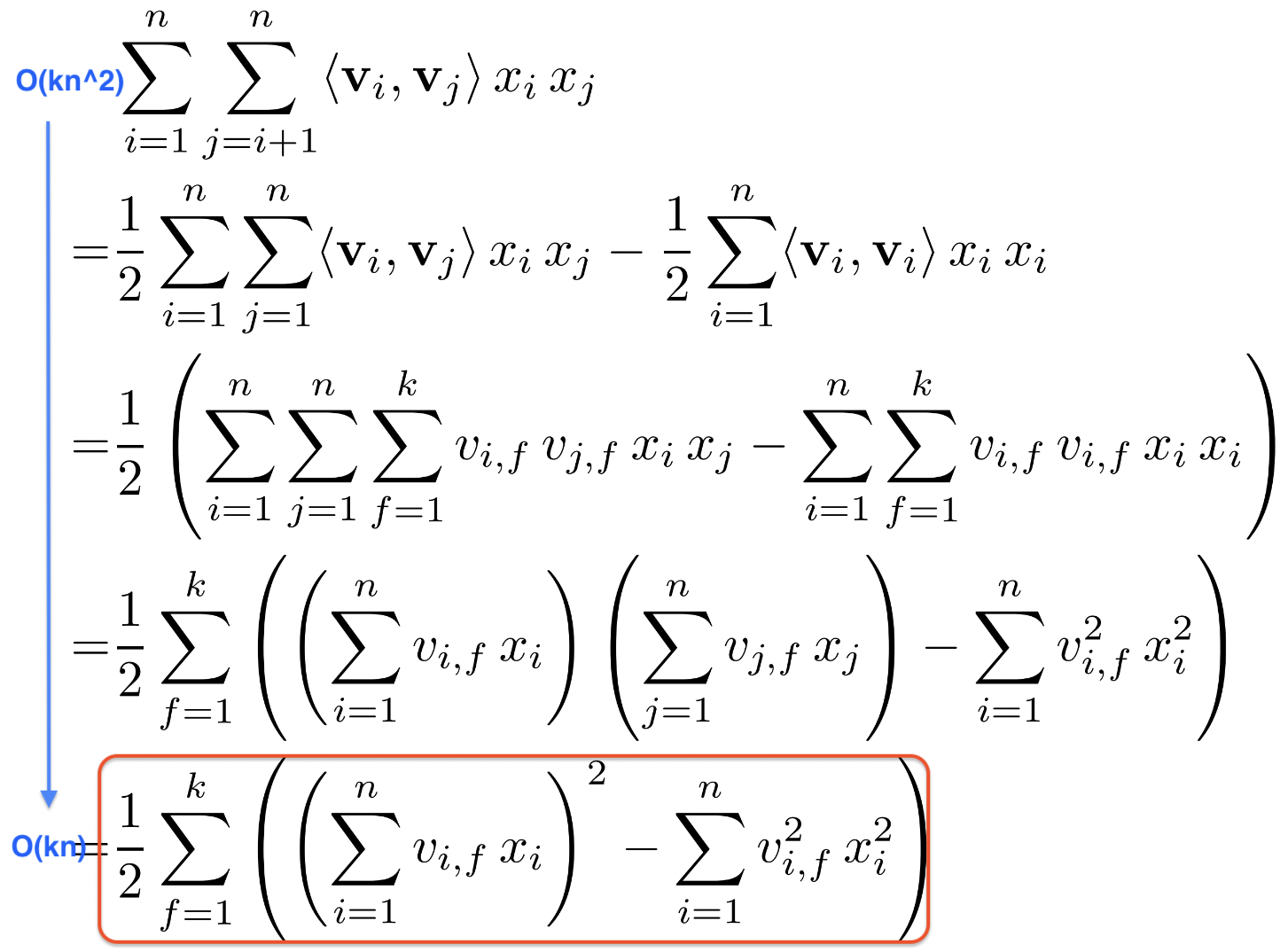
Factorization of pairwise interaction
2개 변수에 직접적으로 연관있는 model parameter가 없다
Pairwise interaction 식을 정리하면 다음과 같다
- 코드 상, 맨 마지막 식이 잘 구현되어야 linear complexity를 가질 수 있음!

Factorization Machine as Predictors

FM의 또다른 장점 ➡️ general predictor로써의 역할
L2 정규화 텀을 넣어서 오버피팅 방지 (다른 오버피팅 방지 기법도 활용 가능)

Learning Factorization Machine

Factorization Machine을 어떻게 학습시키는지
$\hat{y}$ 의 미분을 세타 값에 따라 다음과 같이 3가지로 나눔
이러한 gradiente들을 업데이트하면서 모델이 학습되겠지
마지막 sum 부분은 $i$ 에 독립적이고 미리 계산가능함 ➡️ time complexity가 더 떨어진다

d-way Factorization Machine

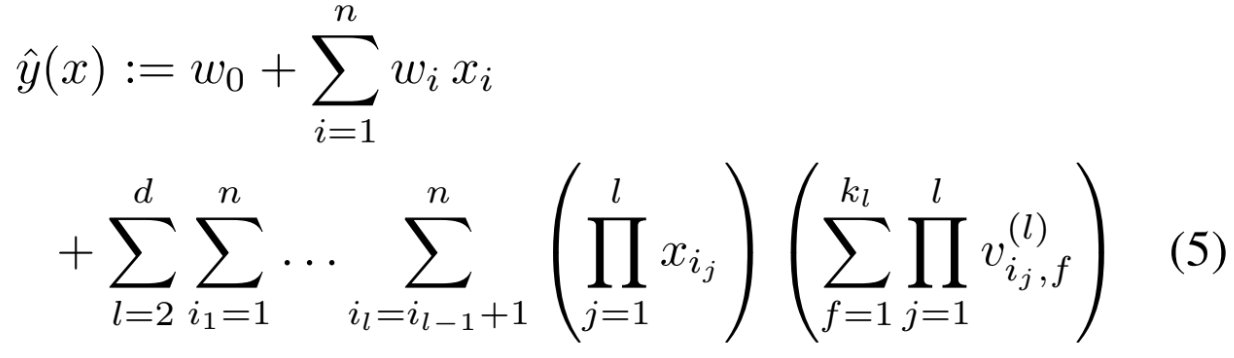
2-way FM을 d-way FM으로 일반화 가능
마찬가지로 computaiton cost는 linear함
http://www.libfm.org 에 다양하게 활용할 수 있는 module 공개되어 있음

Additional Experiments

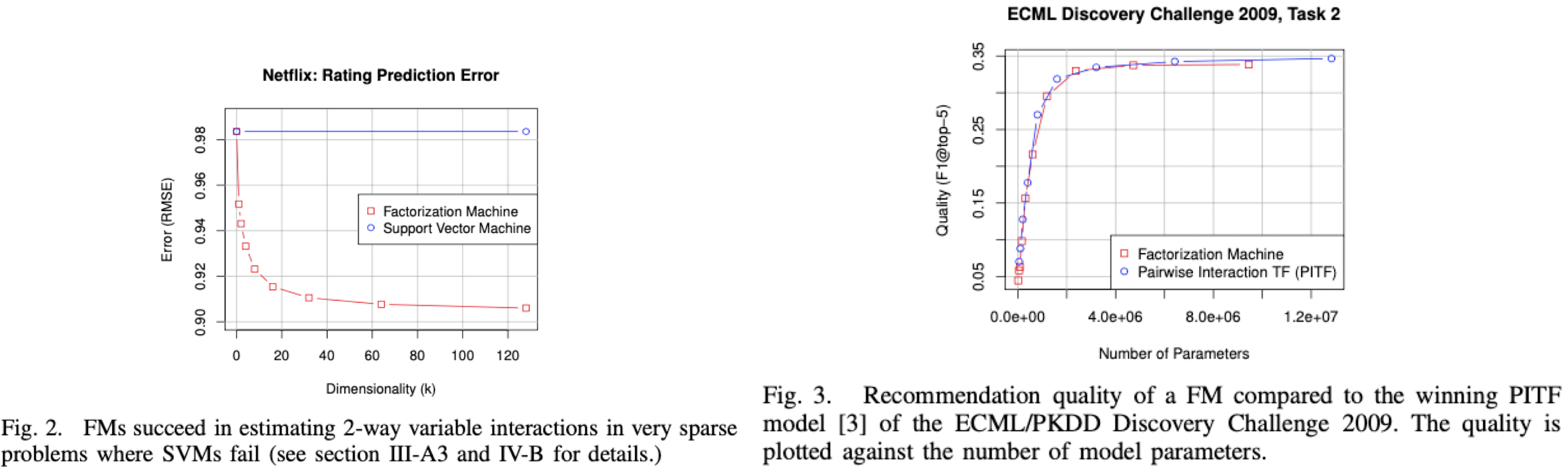
추가적으로 SVM, PITF(Pairwise Interaction TF) model과 비교한 실험도 많음
간단하게 설명하면, FM 모델이 general predictors로써 general하게 적용된다는 것 증명함
Fig 2. SVM은 차원 변화에 따라 error 값 변화가 없지만 저자가 제안한 FM 모델은 error 값이 점점 떨어져 학습이 더 잘 된다는 것
Fig 3. F1-score에 따른 FM과 PITF 성능을 비교한 그래프인데, 당시 PITF 모델은 그 당시의 SOTA 모델이었음. 그런데 FM과 동일한 퍼포먼스를 보임을 증명

Conclusion

1. Factorized Interaction을 사용하여 feature vector x의 모든 가능한 interaction을 모델링한다

Factorized Interaction: Model Equation에서 변수간 interation을 구할 때 latent vector를 조합한다는 내용

2. (High) sparse한 상황에서 interaction을 추정 가능하다. Unobserved interaction에 대해서도 일반화 가능

(Model Equation의 맨 마지막 항) sparsity 데이터를 튜플처럼 만들어서 모든 interaction을 얻을 수 있다. unobserved interaction도 $x_ix_j$ 을 통해 모든 interaction을 보기 때문에 우리가 미처 발견하지 못한 interaction도 일반화해서 추천에 사용 가능

3. 파라미터 수, 학습과 예측 시간 모두 linear하다 (Linear Complexity)

4. 이는 SVD를 활용한 최적화를 진행할 수 있고, 다양한 loss function을 사용할 수 있다.

4. SVM, matrix, tensor and specialized factorization model보다 더 나은 성능을 증명했다.

Recap

우리가 중요하게 기억해야 할 key point 3가지

feature vector $x$ 를 만들어서 활용한다.
FM은 (High) Sparse data에도 잘 작동한다.
Linear Complexity하다.

따라서 prediction에서 general하게 작동하여 꼭 추천에만 국한된 것이 아니라, 다른 머신러닝 문제에서도 적용해볼 수 있는 좋은 알고리즘이라고 생각함!

Yeonghyeon

Ch 08-4. Factorization Machine