문제

12015번: 가장 긴 증가하는 부분수열 2

풀이

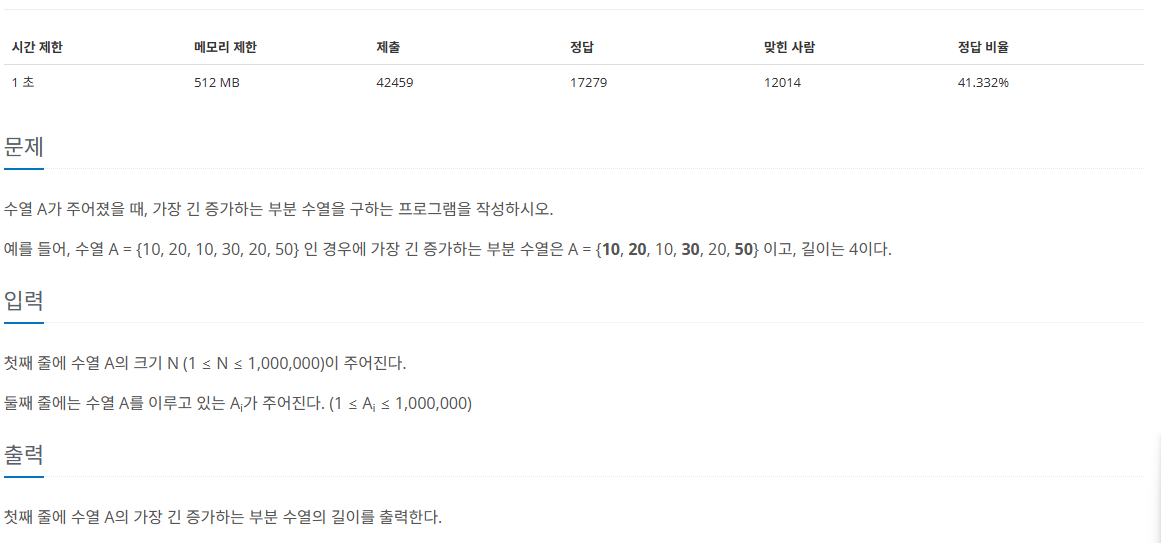
문제에서 요구하는 바는 가장 긴 증가하는 부분수열과 동일하지만 조건이 다르다. N이 최대 1,000,000까지 가능하여 $O(n^2)$의 풀이로는 해결할 수 없다.

예를 들어 배열이 {10, 20, 30, 15, 20, 30, 50, 40, 45 ,60}으로 주어졌다.
입력을 하나씩 받으며 부분수열을 구해갈 수 있다.
{10}
{10, 20}
{10, 20, 30}
하지만 그 다음 15가 나오면서 30보다 크지 않아 추가할 수 없다.

부분수열의 마지막보다 크지 않은 수가 나오게 될 경우 처리하는 방법이 다르다.
우리가 구해야 하는 부분수열이 가장 길어야 한다. 제한된 크기의 숫자에서 수열이 길기 위해선 수 사이의 간격이 최대한 작아야 한다.
따라서 10과 20사이의 간격보다 10과 15사이의 간격이 더 좁으니 20을 15로 대치할 수 있겠다.
그 다음 수 20이 들어오면 30과 대치할 수 있다.

이렇게 모든 수에 대해서 위의 과정을 반복하면 완성된 수열은 {10, 15, 20, 30, 40, 45, 60}을 구할 수 있다.

하지만 한가지 의문이 생길 수 있다.
만약 배열이 {10, 20, 30, 15}로 주어진다면 {10, 15, 30}으로 15가 30보다 뒤에 있는데 완성된 수열이 어떻게 15, 30 순서로 존재할 수 있는가이다.
물론 문제에서 가장 긴 증가하는 부분수열을 구하라고 했다면 틀린 답이되지만, 부분수열의 길이를 출력하는 문제이기 때문에 대치하여 해결하는 풀이 방법이 문제되지 않는다.

이제 남은 문제는 대치할 위치를 어떻게 찾을 지이다.
배열의 다음 수a가 부분수열의 마지막 수 보다 크지 않을 경우에
부분수열 내부에서 a보다 크거나 같은 수 중 가장 작은 수와 대치한다.
이는 이분탐색으로 통해 찾을 수 있다.

코드

#include <iostream>
#include <vector>

using namespace std;


int main()
{
    cin.tie(0);
    ios_base::sync_with_stdio(false);

    int n;
    cin >> n;
    vector<int> arr;
    for (int i=0; i<n; ++i)
    {
        int input;
        cin >> input;
        
        if (arr.empty() || arr.back() < input)
        {
            arr.push_back(input);
            continue;
        }

        // binary search
        int lo = 0; 
        int hi = arr.size()-1;
        while (lo <= hi)
        {
            int mid = (lo + hi) / 2;
            if (input <= arr[mid]) // input 보다 크거나 같은 수가 처음 나오는 경우를 찾는다.
                hi = mid - 1;
            
            else
                lo = mid + 1;
            
        }
        
        arr[lo] = input;
    }

    cout << arr.size() << endl;
    return 0;
}

참고

https://st-lab.tistory.com/285