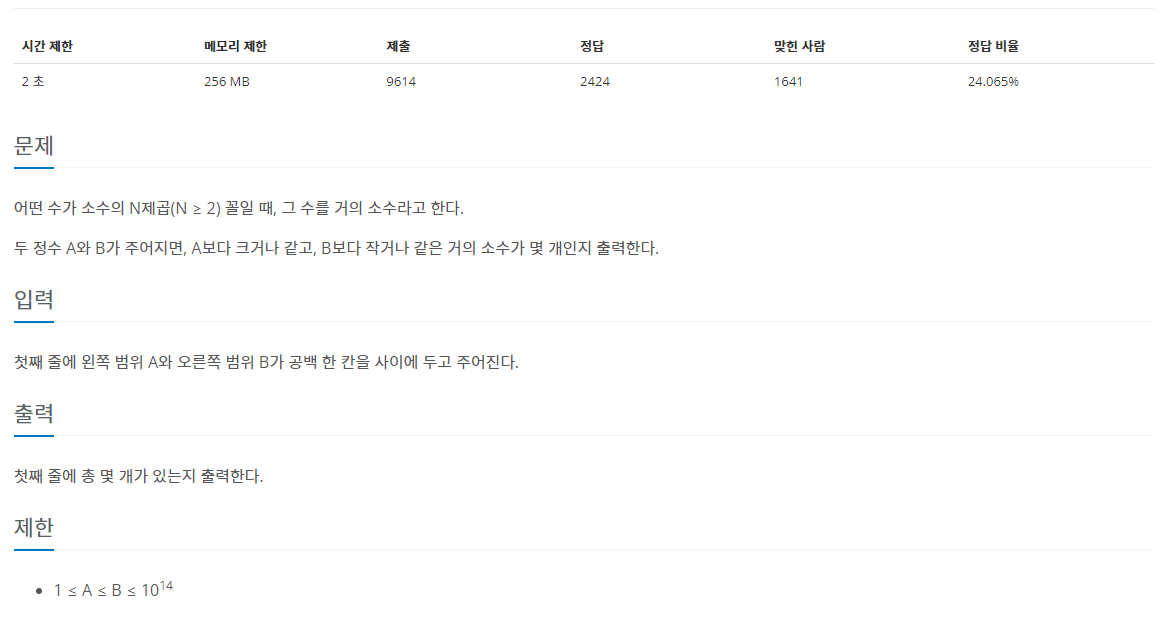
문제

1456번: 거의 소수

풀이

에라토스테네스의 체를 사용하여 B보다 작은 소수들을 구하며 그의 제곱들을 하나씩 세주면 되는 문제이다.

간단해 보이지만 10의 14제곱의 수를 처리해야 하는 만큼 정말 큰 수를 처리해야 해서
integer overflow가 발생하지 않도록 주의해야 한다.

만약 $10^7$에 근접한 소수가 있다면 그의 제곱은 $10^{14}$, $10^{21}$ 처럼 정말 큰 수를 b와 비교해야 한다. 그런데 $10^{21}$은 LLONG_MAX보다 큰 수이므로 변수에 담을 수 없어 제대로된 비교가 되지 않는다.
따라서 이를 위해 비교해야 할 값 pow를 LLONG_MAX / i와 비교하여 pow * i가 LLONG_MAX보다 커지지 않도록 처리해야 한다.

46프로 '틀' 인분들에게 참고가 될 글일 수도 있습니다.

코드

#include <iostream>
#include <vector>
#include <cmath>
#include <climits>

using namespace std;

int main () {
    int64_t a,b;
    cin >> a >> b;

    int64_t sqrtB = (int64_t)sqrt(b);
    vector<bool> isNotPrime(sqrtB+1, false);
    int64_t answer = 0;

    for (int i=2; (int64_t)i*i <= b; i++){
        if (isNotPrime[i]) continue;
        for (int j=i*2; (int64_t)j*j <= b; j += i){
            isNotPrime[j] = true;
        }
        int64_t pow = (int64_t)i*i;
        while (pow <= b){
            if (pow >= a){
                answer += 1;
            }
            if (pow > LLONG_MAX / i) break;
            pow *= i;
        }
    }
    cout << answer << endl;
}