문제

1561번: 놀이 공원

풀이

이전에 프로그래머스에서 이 문제와 유사한 입국심사문제를 풀어본 적이 있어서 이분 탐색 문제라는 것을 눈치챌 수 있었다.

이분 탐색(매개변수 탐색) 문제이기 위해서는 탐색에 사용하는 수(매개변수), 그 수에 대응하는 비교할 값(함수 값)이 존재해야 하고 증가하거나 감소하기만 해야한다.

임의의 세 수 $a,b,c$에 대해 $a < b < c$이 만족한다면 아래의 식이 만족해야 한다.

$f(a) \le f(b) \le f(c) \\ or \\ f(a) \ge f(b) \ge f(c)$

예를 들어 아래의 그림처럼 함수 값이 계산된다면 이분탐색이 가능하다.




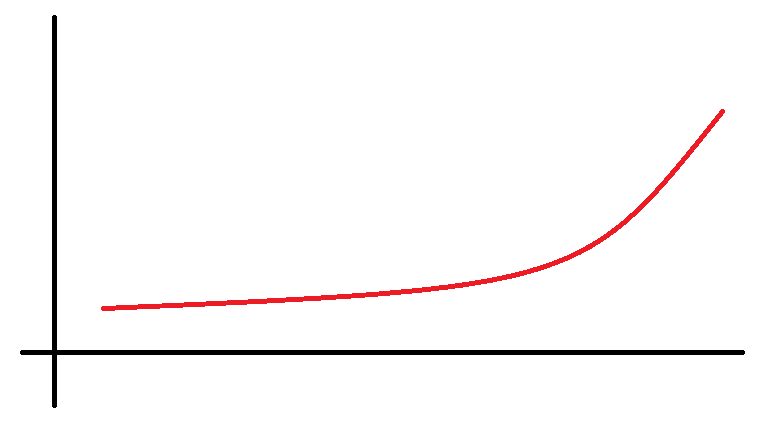
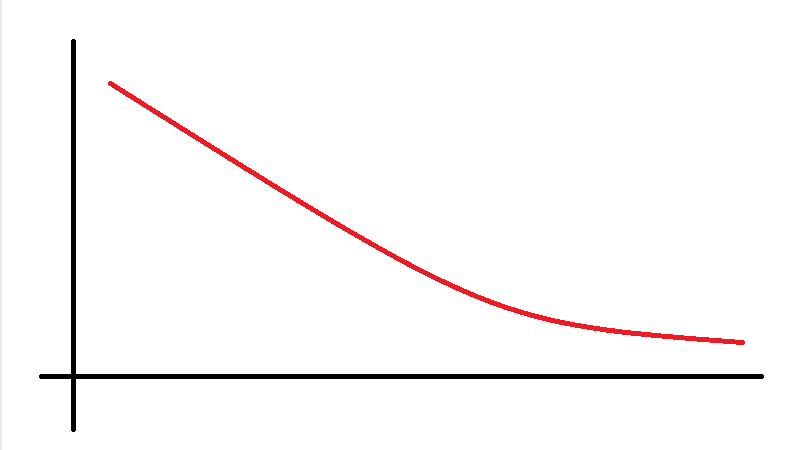
하지만 아래의 그림처럼 함수 중간에 기울기의 부호가 변경되는 지점이 발생한다면 이분탐색으로 찾을 수 없다.

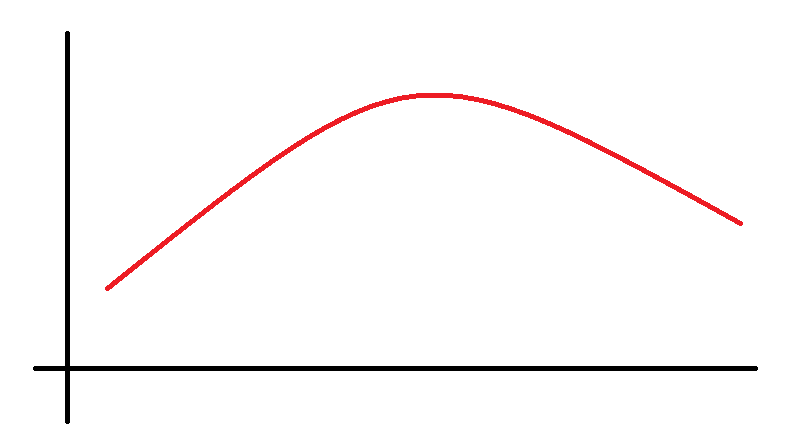
이번 문제에서는 매개변수로 시간, 함수의 결과값으로 해당 시간에 놀이기구를 이용한 학생 수로 두고 문제를 해결하였다.
시간이 증가 할수록 놀이기구를 이용한 학생의 수 또한 증가하므로 이분탐색이 가능하다.

시간에 대한 놀이기구 이용 학생의 수를 정확히 정의해야 문제를 헷갈리지 않고 해결할 수 있다.
나는 f(시간)을 해당 시점에서 놀이기구 이용을 완료한 학생의 수 + 현재 놀이기구를 이용하고 있는 학생의 수라고 정의했다.

따라서 각 놀이 기구에 대해서

• 현재 시점에 놀이기구가 운행 중이라면,
  현재 시간 / 놀이기구 운행 시간 + 1(현재 이용중인 학생)
• 운행 종료(완료)되었다면,
  현재 시간 / 놀이기구 운행 시간 + 0

이를 코드로 작성한다면

int64_t countChild(int64_t currentTime){
    int64_t child = 0;
    for (int i=0; i < times.size(); i++){
        currentTime % times[i] == 0 
        ? child += currentTime / times[i]
        : child += currentTime / times[i] + 1;
    }
    return child;
}

함수를 정의 했으니 함수의 결과값을 비교하며 이분탐색이 가능하다.
입력으로 주어진 학생의 수(N)보다 크거나 같은 시점의 시간을 이분탐색으로 알 수 있다.
다시 말하면 놀이 기구를 이용한 학생의 수가 N보다 큰거나 같은 시간의 최소값을 구할 수 있다.
그 시간을 curTime이라 한다면 curTime-1은 N보다 적은 수의 학생들이 놀이기구를 이용한 것이다.

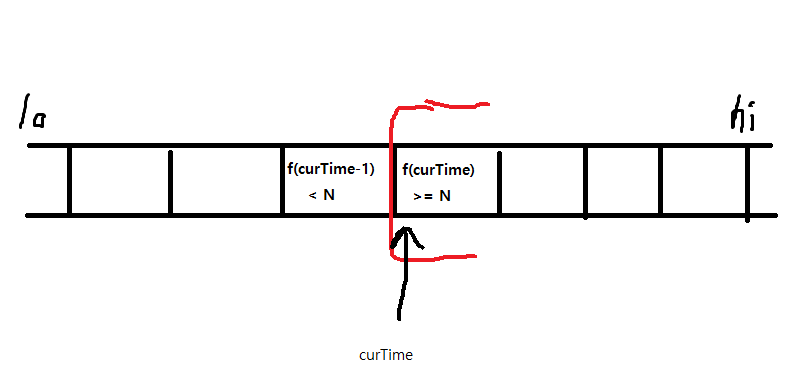
curTime 시점의 학생 수는 N과 정확히 일치하지 않고 N보다 큰 경우도 있다.
따라서 N을 정확히 계산하기 위해서는 curTime-1 시점에서부터 남은 학생의 경우의 수를 찾아가며 N번째 학생의 놀이기구를 찾아야 한다.
curTime-1 시점에서 운행하고 있지 않은 놀이기구를 한명씩 채워가며 경우의 수를 찾을 수 있다.

curTime-1이 시점에서의 학생 수 + 남은 학생의 수 = curTime의 학생 수 이므로
운행하고 있지 않은 놀이기구 중 남은 학생의 수번째의 인덱스를 구한다면 마지막 학생의 놀이기구를 구할 수 있다.

int64_t targetTime = curTime - 1;
int64_t curChild = countChild(targetTime);
int64_t remainedChild = n - curChild;
for (int i=0; i<times.size(); i++){
    if (targetTime % times[i] == 0 && --remainedChild == 0){
        cout << i+1 << endl;
        break;
    }
}

코드

#include <iostream>
#include <vector>

using namespace std;

int64_t n, m;
vector<int> times;

int64_t countChild(int64_t currentTime){
    int64_t child = 0;
    for (int i=0; i < times.size(); i++){
        currentTime % times[i] == 0 
        ? child += currentTime / times[i]
        : child += currentTime / times[i] + 1;
    }
    return child;
}

bool check(int64_t mid){
    return countChild(mid) >= n;
}

int main() {
    cin.tie(0);
    ios_base::sync_with_stdio(false);

    cin >> n >> m;
    times = vector<int>(m);
    for (int i=0; i < m; i++) { cin >> times[i]; }
    
    int64_t lo = 0;
    int64_t hi = n * 30;
    while (lo<=hi){
        // cout << lo << " " << hi << endl;
        int64_t mid = (lo + hi) / 2;
        if (check(mid)){
            hi = mid-1;
        }
        else {
            lo = mid+1;
        }
    }

    int64_t curTime = lo;
    int64_t targetTime = curTime - 1;
    int64_t curChild = countChild(targetTime);
    int64_t remainedChild = n - curChild;
    for (int i=0; i<times.size(); i++){
        if (targetTime % times[i] == 0 && --remainedChild == 0){
            cout << i+1 << endl;
            break;
        }
    }

    return 0;
}

이분 탐색은 항상 머리가 아프다.

• 함수 결과값이 비교값과 크거나 같을때의 매개변수의 최소값을 구하기 위해 최종 변수 = lo (문제)
• 함수 결과값이 비교값과 작거나 같을때의 매개변수의 최대값을 구하기 위해 최종 변수 = hi

두 가지 경우를 정리할 수 있었는데, 함수가 증가 함수가 아닌 감소 함수인 경우에 대해서도 적용되는지 확인이 필요하다.