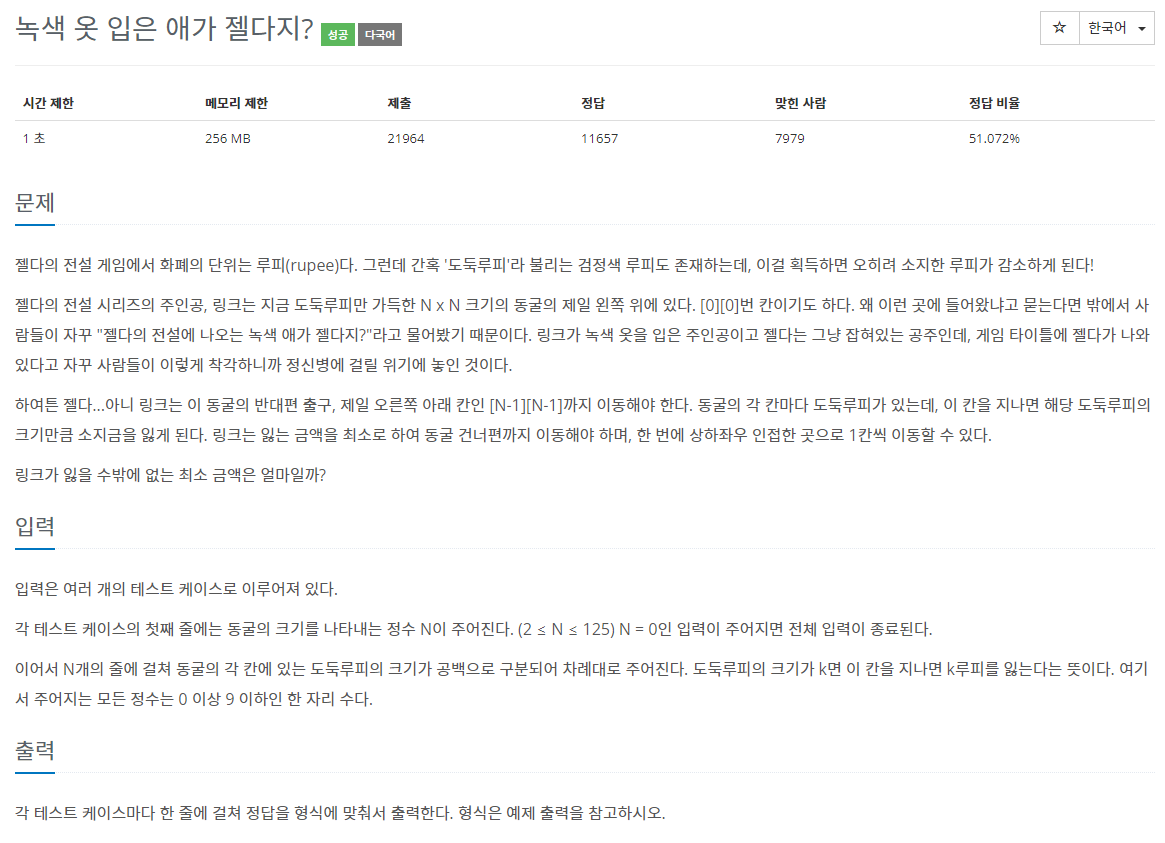
문제

4485번: 녹색 옷 입은 애가 젤다지?

풀이

소지금을 최대한 적게 잃기 위해 지나가는 각 칸의 도둑루피의 합이 최소이어야 한다.
이를 위해 다익스트라 알고리즘을 사용하여 해결하였다.
각 칸의 십자 방향으로 인접한 칸을 연결된 노드로 보고,
그 칸의 도둑루피 값을 가중치로 하여 최단거리 알고리즘을 적용한다.

코드

#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>

#define INF 9 * 125 * 125 +1

using namespace std;

struct Pos {
    int x;
    int y;
    
    bool operator==(Pos& input) { return x == input.x && y == input.y; }
    Pos operator+ (Pos& input) {
        Pos res;
        res.x = x + input.x;
        res.y = y + input.y;
        return res;
    }
};

struct Node {
    Pos pos;
    int weight;

    bool operator> (Node& input) { return weight > input.weight; }
};

struct cmp {
    bool operator() (Node& a, Node& b) { return a > b; }
};

vector<Pos> delta { {0, 1}, {1, 0}, {0, -1}, {-1, 0}};
vector<vector<int>> dist;
vector<vector<int>> cave;

bool OOB(const Pos& pos, int n){
    return pos.x < 0 || pos.x >= n || pos.y < 0 || pos.y >= n;
}

int dijkstra (Pos start, int n){

    priority_queue<Node, vector<Node>, cmp> pq;
    int startWeight = cave[start.x][start.y];
    pq.push({ start, startWeight });
    dist[start.x][start.y] = startWeight;

    while (!pq.empty()){
        Pos curPos = pq.top().pos;
        int weight = pq.top().weight;
        pq.pop();

        if (dist[curPos.x][curPos.y] < weight) continue;
        // if (curX == n-1 && curY == n-1) break;
        for (auto del : delta){
            Pos nextPos = curPos + del;
            if ( OOB(nextPos, n) ) continue;
            int nextWeight = weight + cave[nextPos.x][nextPos.y];

            if ( dist[nextPos.x][nextPos.y] > nextWeight ){
                dist[nextPos.x][nextPos.y] = nextWeight;
                pq.push({ nextPos, nextWeight });
            }
        }
    }
    return dist[n-1][n-1];
}

int main(){
    cin.tie(0);
    ios_base::sync_with_stdio(false);

    bool flag = true;
    int n;
    vector<int> answer;

    while (flag){
        cin >> n;
        if (n == 0) break;

        cave = vector<vector<int>> (n, vector<int>(n));
        dist = vector<vector<int>> (n, vector<int> (n, INF));
        for (int i=0; i < n; i++){
            for (int j=0; j < n; j++){
                cin >> cave[i][j];
            }
        }

        answer.push_back( dijkstra( {0,0}, n) );
    }

    for (int i=0; i < answer.size(); i++){
        printf("Problem %d: %d\n", i+1, answer[i]);
    }

    return 0;
}