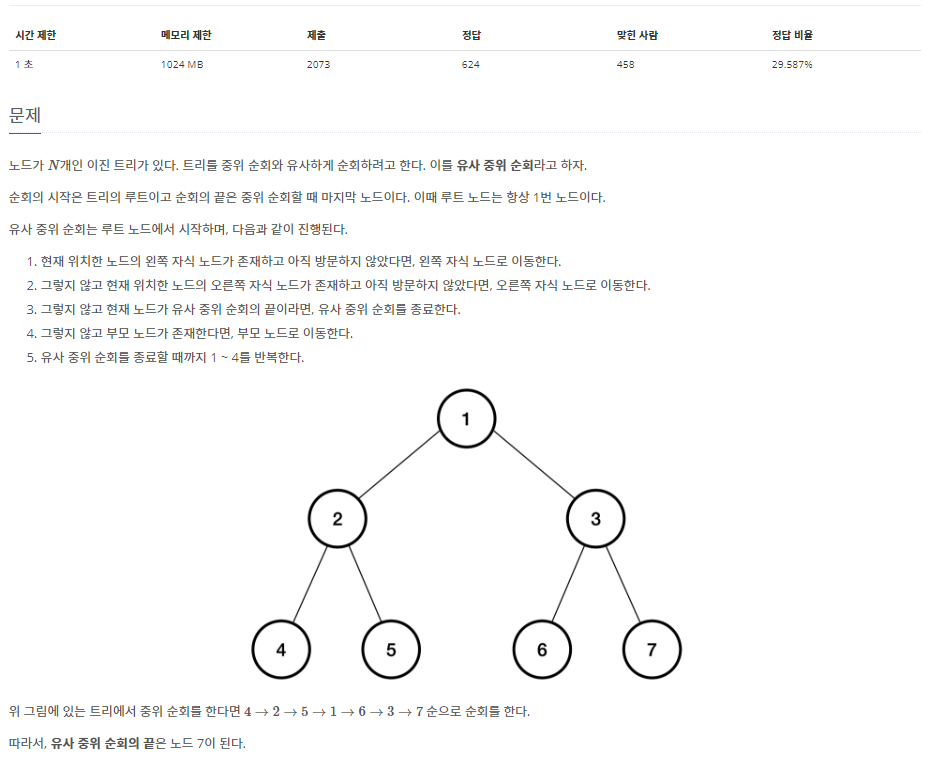
문제

22856번: 트리 순회

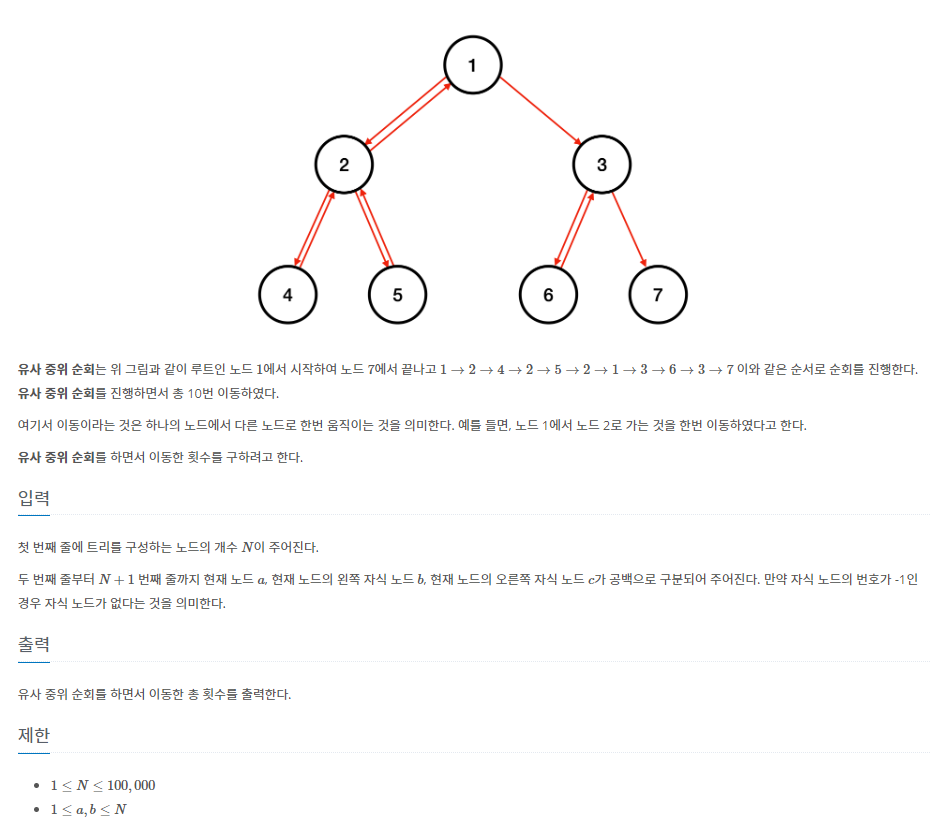
풀이

문제가 복잡해 보이지만 결과적으로 몇번 움직이는지만 안다면 간단한 문제다.
루트에서 중위 순회의 마지막 노드를 가는 경로를 제외하고는 모든 노드를 탐색 후 부모 노드로 돌아가야 하므로
(트리의 간선의 수 * 2) - (루트에서 중위 순회 마지막 노드로 가는 경로의 간선 수)로 구할 수 있다.

이진 트리의 간선의 수는 노드의 개수 -1이다.

코드

#include <iostream>
#include <vector>

using namespace std;

typedef pair<int, int> child_t;
int n;
vector<child_t> graph;

int main () {
    cin.tie(0);
    ios_base::sync_with_stdio(false);

    cin >> n;
    graph = vector<child_t>(n+1);
    for (int i=0; i<n; i++){
        int a, b, c;
        cin >> a >> b >> c;
        graph[a].first = b;
        graph[a].second = c;
    }

    int lastNode = 1;
    int cnt = 0;
    while (graph[lastNode].second != -1) {
        cnt++;
        lastNode = graph[lastNode].second;
    }
    cout << (n -1) * 2 - cnt << endl;
}