문제

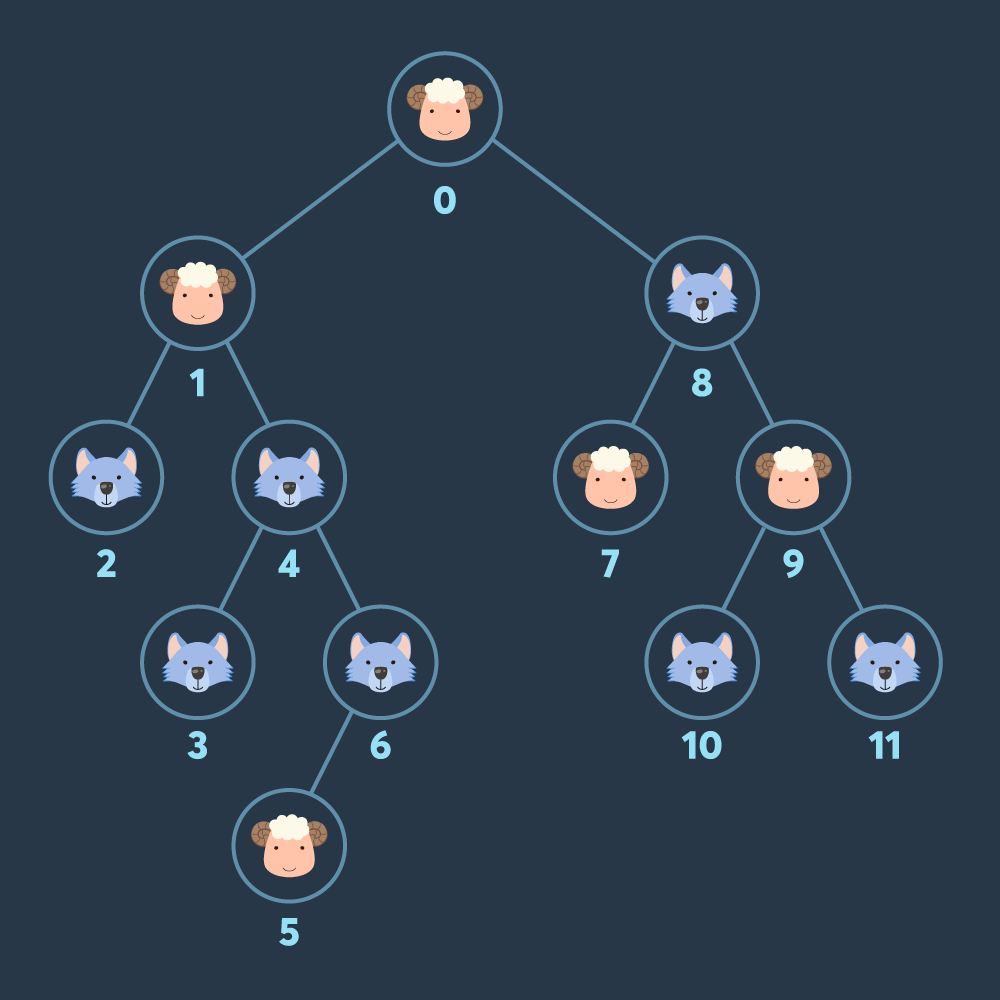
2진 트리 모양 초원의 각 노드에 늑대와 양이 한 마리씩 놓여 있습니다. 이 초원의 루트 노드에서 출발하여 각 노드를 돌아다니며 양을 모으려 합니다. 각 노드를 방문할 때 마다 해당 노드에 있던 양과 늑대가 당신을 따라오게 됩니다. 이때, 늑대는 양을 잡아먹을 기회를 노리고 있으며, 당신이 모은 양의 수보다 늑대의 수가 같거나 더 많아지면 바로 모든 양을 잡아먹어 버립니다. 당신은 중간에 양이 늑대에게 잡아먹히지 않도록 하면서 최대한 많은 수의 양을 모아서 다시 루트 노드로 돌아오려 합니다.

문제 링크: 프로그래머스-양과 늑대

풀이

• 탐색할 수 있는 모든 경우의 수를 따져가며 최대한 많은 양을 모아야 한다.
• 루트 노드부터 늑대보다 양이 많은 경우를 계속 탐색해야 한다.
• 탐색하는 순서가 달라도 결과가 같다면 같은 탐색으로 분류하여 중복 탐색을 제거한다.
  • 탐색 결과가 처음이 아니라면(해당 결과를 이전에 확인한적이 있다면) 아무것도 하지 않고 넘어간다.
  • 노드를 이전에 방문했는지를 확인하는 것이 아닌 결과를 이전에 확인한적이 있는지를 검사해야 한다.
• 탐색 결과가 조건(양의 수> 늑대의 수)에 맞다면 해당 결과에서 갈 수 있는 경우의 수를 다시 탐색한다.

탐색전 graph를 만들어서 노드번호를 인덱스로 바로 접근할 수 있도록 했다.

vector<node> graph(info.size(), {-1,-1,0});
    for (auto i: edges) {
        int p = i[0];
        int c = i[1];
        if (graph[p].left == -1){
            graph[p].left = c;
        }
        else{
            graph[p].right = c;
        }
    }
    for (int i=0; i < info.size(); i++){
        graph[i].value = info[i];
    }

중복 탐색을 제거하기 위해 비트마스킹을 이용했다.

vector<bool> visited( 1<<info.size() );

탐색 결과가 모든 조건을 만족하여 새로운 노드를 탐색하기 위해서 루트노드부터 모든 노드를 돌면서 그 자식을 포함하여 다시 탐색한다. 이때 엄청난 중복이 발생하는데 이를 visited를 이용하여 관리한다.

코드

#include <string>
#include <vector>

using namespace std;

struct node {
    int left;
    int right;
    int value;
};

void dfs(const vector<node>& graph, int v, 
  vector<bool>& visited, int& answer) {
  
    if (visited[v]){
        return;
    }
    visited[v] = true;
    int sheep = 0;
    int wolf = 0;

    for (int i=0; i < graph.size(); i++){
        if (v & (1 << i)){
            sheep += graph[i].value ^ 1;
            wolf += graph[i].value;
        }
    }

    if (sheep <= wolf) {
        return;
    }

    answer = answer < sheep ? sheep : answer;

    for (int i=0; i < graph.size(); i++){
        if (v & (1 << i)){
            if (graph[i].left != -1){
                dfs(graph, v | (1 << graph[i].left), visited, answer);
            }
            if (graph[i].right != -1){
                dfs(graph, v | (1 << graph[i].right), visited, answer);
            }
        }
    }

}

int solution(vector<int> info, vector<vector<int>> edges) {
    int answer = 0;
    vector<bool> visited( 1<<info.size() );
    vector<node> graph(info.size(), {-1,-1,0});
    for (auto i: edges) {
        int p = i[0];
        int c = i[1];
        if (graph[p].left == -1){
            graph[p].left = c;
        }
        else{
            graph[p].right = c;
        }
    }
    for (int i=0; i < info.size(); i++){
        graph[i].value = info[i];
    }


    dfs(graph, 1, visited, answer);
    return answer;
}

중복이 많이 발생한는 것을 visited로 관리하는 것이 dp의 메모이제이션과 비슷하다 생각했다.

어떻게 풀어야할지 감도 안잡히고 손도 못대던 문제여서 많은 사람들의 풀이를 읽어봤다. 읽던 중 가장 마음에 드는 풀이를 발견했고 참고하여 풀었다.
사실 거의 그대로 배낀 수준이라 너무 아쉽다.