접근
분할 정복은 큰 문제를 작은 문제로 나눌 수 있는 경우에 적용하면 좋고, 동적 계획법(Dynamic programming)은 작은 문제의 답을 큰 문제 해결에 재활용할 수 있는 경우에 적용하면 좋다. 그래서 동적 계획법을 상향식(Bottom-up) 프로그래밍이라고 부르기도 한다.
그 대표적인 예시가 이항 계수 계산이다. (n, k)의 이항 계수는 (n - 1, k - 1) + (n - 1, k)의 합이기 때문에, 작은 문제부터 계산해서 큰 문제의 답을 구하기에는 최적화된 문제다.
(단, 이 글에서는 n >= k인 경우만 따지도록 한다.)
Python 코드
재귀 (Recursion)
def binomial_coefficient_recursion(n: int, k: int) -> int:
if (n == k) or (k == 0): return 1
else:
left = binomial_coefficient_recursion(n - 1, k - 1)
right = binomial_coefficient_recursion(n - 1, k)
return left + right쉽다. 이항 계수의 계산식을 그대로 코드로 변환하면 된다. 그러나 재귀 특성상 아마 시간이 굉장히 오래 걸릴 것이다.
동적 계획법 (Dynamic programming)
import copy
def binomial_coefficient_dp(n: int, k: int) -> int:
if (n == k) or (k == 0): return 1
else:
matrix = [copy.deepcopy([0] * (n + 1)) for _ in range(k + 1)]
x = 0
y = 0
while True:
to_next_line = False
# 값 채우기
if (x == y):
matrix[x][y] = 1
to_next_line = True
elif (x == 0):
matrix[x][y] = 1
elif (x == k):
matrix[x][y] = matrix[x - 1][y - 1] + matrix[x][y - 1]
to_next_line = True
else:
matrix[x][y] = matrix[x - 1][y - 1] + matrix[x][y - 1]
# 이동
if (x == k) and (y == n):
break
elif (to_next_line):
x = 0
y += 1
else:
x += 1
return matrix[k][n]주요 포인트가 몇 개 있다:
깊은 복사: copy 패키지의 deepcopy() 함수
이항 계수 계산을 위해 행렬을 생성하면서, 깊은 복사를 제공하는 copy 패키지의 deepcopy() 함수를 사용했다.
Python의 리스트 자료형은 copy() 메소드를 제공하긴 하는데, 이건 얕은 복사라서 이번 문제에서는 사용할 수 없다. copy() 메소드를 쓸 경우, 첫 번째 세로줄의 내용을 바꾸면 건들지 않은 두 번째, 세 번째, ...등 모든 세로줄의 내용도 동일하게 바뀌는 문제가 발생한다.
메모리 공간 줄이기
동작을 1) 행렬 칸의 값을 계산하고 2) 다음 좌표를 계산하는 두 단계로 구성했다.
사실 단순하게 하려면, 그냥 n * n 크기의 정사각형 배열을 생성하고 x와 y가 같을 때 다음 줄로 넘어가는 식으로 구현해도 된다. 근데 그러면 1) 답을 구할 때 필요하지 않은 더미 데이터에 대해서도 계산이 진행되어야 하고 2) 계산된 더미 데이터가 행렬에서 차지하는 공간으로 인해 메모리 공간도 조금 더 많이 쓰게 된다.
소모를 좀 줄이기 위해서 행렬 값 계산과 다음 좌표 계산을 조건문으로 세세하게 구현해 효율성을 높였다.
시간 복잡도
n = 5, k = 3일 때, 연산 횟수는 아래 표와 같다:
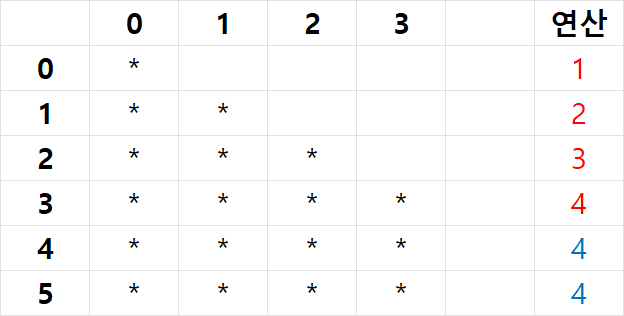
요악하면 아래 두 개를 더한 값이 연산 횟수다:
- 1부터 k + 1을 더한 값
- n - k에 k + 1을 곱한 값
W(n, k) = (k = 1)(k + 2)/2 + (n + k)(k + 1)이고, 전개하면 k의 제곱과 nk 항이 존재한다. n이 k보다 크거나 같기 때문에 k의 제곱은 무시되고, W(n, k) = O(nk)이다.
