[백준]10844 쉬운 계단 수

iamjinseo·2022년 7월 6일

다이나믹 프로그래밍 백준

문제풀이-Python

목록 보기

14/134

문제

45656이란 수를 보자.

이 수는 인접한 모든 자리의 차이가 1이다. 이런 수를 계단 수라고 한다.

N이 주어질 때, 길이가 N인 계단 수가 총 몇 개 있는지 구해보자. 0으로 시작하는 수는 계단수가 아니다.

입출력

입력

첫째 줄에 N이 주어진다. N은 1보다 크거나 같고, 100보다 작거나 같은 자연수이다.

출력

첫째 줄에 정답을 1,000,000,000으로 나눈 나머지를 출력한다.

입출력 예시

해설

예시 - 자리수 3일 때(N이 3일 때)

1) 계단수를 구하기 위해서는 맨 뒷자리 수를 제외한 나머지 두 자리 수의 계단수들이 필요하다.
2) 두 자리 수들의 계단수를 구하기 위해서는 맨 뒷자리 수를 제외한 한 자리 수의 계단수들이 필요하다
3) 한 자리 수들의 경우의 수를 구한다. 1 2 3 4 5 6 7 8 9가 있으므로 경우의 수는 9이다. 그리고 0부터 9까지의 수가 맨 뒷자리로 오는 경우를 테이블에 넣어본다.=> 0 1 1 1 1 1 1 1 1 1
4) 두 자리 수 계단수의 경우의 수를 구한다.

맨 뒷자리가 0일 때) 0 앞에는 1만 올 수 있으므로 10과 같은 결과가 나온다. 그렇다면 자리수가 한 자리수였을 때 1이 맨 뒤로 오는 경우의 수가 0이 맨 뒤로 오는 경우의 수이다. 경우의 수는 1이다.
맨 뒷자리가 1일 때) 1 앞에는 0과 2가 올 수 있으나 0은 맨 앞에 올 수 없다는 규칙이 있다. 따라서 21과 같은 결과가 나온다. 그렇다면 자리수가 한 자리수였을 때 2가 맨 뒤로 오는 경우의 수는 1이므로 경우의 수는 1이다.
...

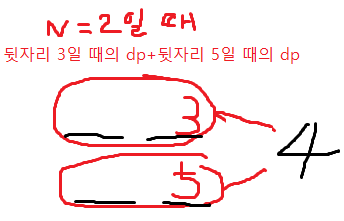
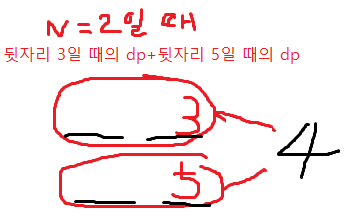
5) 세 자리 수 계단수의 경우의 수를 구한다.

맨 뒷자리가 4일 때 앞에는 3과 5가 올 수 있다. 그렇다면 자리수가 두 자리수였을 때 3이 맨 뒤로 오는 경우의 수와 5가 맨 뒤로 오는 경우의 수를 더하면 되지 않을까? (그림 참고)

코드

# 백준 10844 쉬운 계단 수 / 실버1
# dp

# 인접한 모든 자리 차이가 1이 나는 계단 수 만들기
# N이 주어질 때 길이가 N인 계단 수가 몇 개 있을까?

# 첫째 줄에 N이 주어진다. N은 1이상 100이하
N = int(input())

# 이중 리스트 만들기
dp = [[0]*10 for _ in range(N+1)]

# 자리수가 하나일 때의 경우 집어넣기
for i in range(1, 10):
    dp[1][i] = 1

# 자릿수에 따라, 0~9까지의 수가 맨 뒤에 올 수 있는경우의 수 구하기
for i in range(2, N+1):
    for j in range(0, 10):
        if j==0 : 
            dp[i][j]=dp[i-1][1]
        elif j==9:
            dp[i][j]=dp[i-1][8]
        else:
            dp[i][j]=dp[i-1][j-1]+dp[i-1][j+1]

#첫째 줄에 정답을 1,000,000,000으로 나눈 나머지를 출력한다.
print(sum(dp[N])%1000000000)