[프로그래머스-레벨2]기능개발 - python

iamjinseo·2022년 8월 24일

문제풀이-Python

목록 보기

95/134

https://school.programmers.co.kr/learn/courses/30/lessons/42586#
프로그래머스 팀에서는 기능 개선 작업을 수행 중입니다. 각 기능은 진도가 100%일 때 서비스에 반영할 수 있습니다.

또, 각 기능의 개발속도는 모두 다르기 때문에 뒤에 있는 기능이 앞에 있는 기능보다 먼저 개발될 수 있고, 이때 뒤에 있는 기능은 앞에 있는 기능이 배포될 때 함께 배포됩니다.

먼저 배포되어야 하는 순서대로 작업의 진도가 적힌 정수 배열 progresses와 각 작업의 개발 속도가 적힌 정수 배열 speeds가 주어질 때 각 배포마다 몇 개의 기능이 배포되는지를 return 하도록 solution 함수를 완성하세요.

제한 사항

작업의 개수(progresses, speeds배열의 길이)는 100개 이하입니다.
작업 진도는 100 미만의 자연수입니다.
작업 속도는 100 이하의 자연수입니다.
배포는 하루에 한 번만 할 수 있으며, 하루의 끝에 이루어진다고 가정합니다. 예를 들어 진도율이 95%인 작업의 개발 속도가 하루에 4%라면 배포는 2일 뒤에 이루어집니다.

입출력 예

입출력 예 설명
입출력 예 #1
첫 번째 기능은 93% 완료되어 있고 하루에 1%씩 작업이 가능하므로 7일간 작업 후 배포가 가능합니다.
두 번째 기능은 30%가 완료되어 있고 하루에 30%씩 작업이 가능하므로 3일간 작업 후 배포가 가능합니다. 하지만 이전 첫 번째 기능이 아직 완성된 상태가 아니기 때문에 첫 번째 기능이 배포되는 7일째 배포됩니다.
세 번째 기능은 55%가 완료되어 있고 하루에 5%씩 작업이 가능하므로 9일간 작업 후 배포가 가능합니다.

따라서 7일째에 2개의 기능, 9일째에 1개의 기능이 배포됩니다.

입출력 예 #2
모든 기능이 하루에 1%씩 작업이 가능하므로, 작업이 끝나기까지 남은 일수는 각각 5일, 10일, 1일, 1일, 20일, 1일입니다. 어떤 기능이 먼저 완성되었더라도 앞에 있는 모든 기능이 완성되지 않으면 배포가 불가능합니다.

따라서 5일째에 1개의 기능, 10일째에 3개의 기능, 20일째에 2개의 기능이 배포됩니다.

풀이

from math import ceil
def solution(progresses, speeds):
    days = [] #각 작업당 남은 일수
    for p, s in zip(progresses, speeds):
        days.append(ceil((100-p)/s)) #`(100 - 작업량)/스피드`의 올림이 곧 남은 일수.
        
    res = [] #결과 반환용 리스트
    max = 0 #제일 오래걸리는 날의 인덱스
    for i in range(1, len(days)) :
        if days[i] > days[max] : #어떤 작업이 max보다 오래걸리면
            res.append(len(days[max:i])) #max작업부터 이전까지의 길이(배포 개수) append
            max = i #어떤 작업의 인덱스는 곧 제일 오래걸리는 날
        if i == len(days)-1 : #마지막 작업일 때
            res.append(len(days[max:])) # max작업부터 마지막 작업까지의 배포 개수 append
    return res

days = [] #각 작업당 남은 일수
    for p, s in zip(progresses, speeds):
        days.append(ceil((100-p)/s)) #`(100 - 작업량)/스피드`의 올림이 곧 남은 일수.
각 작업당 남은 일수 구하기
주석 참고. (100 - 작업량)/스피드의 올림은 남은 일수임.
왜냐면 (100 = 작업량+(속도*남은 일수))

res = [] #결과 반환용 리스트
    max = 0 #제일 오래걸리는 날의 인덱스
    for i in range(1, len(days)) :
        if days[i] > days[max] : #어떤 작업이 max보다 오래걸리면
            res.append(len(days[max:i])) #max작업부터 이전까지의 길이(배포 개수) append
            max = i #어떤 작업의 인덱스는 곧 제일 오래걸리는 날
        if i == len(days)-1 : #마지막 작업일 때
            res.append(len(days[max:])) # max작업부터 마지막 작업까지의 배포 개수 append
    return res

스택에 계속 값을 쌓으면서, 이전의 최대 일수보다 더 큰 일수가 나오면 최대 일수부터 더 큰 일수 이전 작업의 개수를 res에 append
그리고 마지막 작업일 때는 남은 걸 전부 반환해야함.

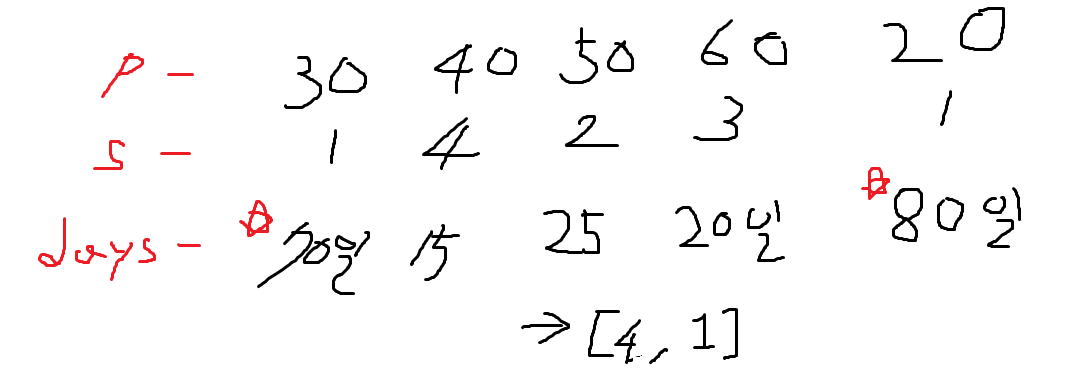
새로운 테스트케이스를 그림으로 그려봤다.

70일짜리 작업을 배포하기 위해, 그 다음의 15일, 25일, 20일짜리 작업들은 대기 상태에 돌입해야 한다.
그러나 80일짜리 작업을 만나면, 70일짜리 작업은 80일짜리가 완수되기 전에 완료된다.
따라서 그 이전의 작업은 전부 배포해야하고, 총 4개가 배포된다.
그리고 가장 오래걸리는 작업은 80일짜리 작업이 되고, 마지막 인덱스에 돌입했을 때 가장 오래걸리는 작업부터 현 작업까지의 개수를 배포한다.

결과

남의 코드

def solution(progresses, speeds):
    Q=[]
    for p, s in zip(progresses, speeds):
    
     #최근에 삽입된 남은 일수가 현재 남은 일수보다 작으면
        if len(Q)==0 or Q[-1][0]<-((p-100)//s): 
            Q.append([-((p-100)//s),1]) #현재 남은 일수와 배포 개수 1삽입
        else: # 최근에 삽입된 남은 일수가 현재 남은 일수보다 크면
            Q[-1][1]+=1 #최근 삽입된 남은 일수에서 배포수 1증가
    return [q[1] for q in Q]

ceil을 안쓰고 올림값을 구현한 게 대단하다... 아래 설명은 댓글에서 퍼옴

math.ceil 없이 올림을 쓰려고 한거 같네요.
(p-100) => 음수, (p-100) // s => 내림한 음수(음수에서 내림은 절대값은 커짐),
-((p-100)//s) => 올림한 양수

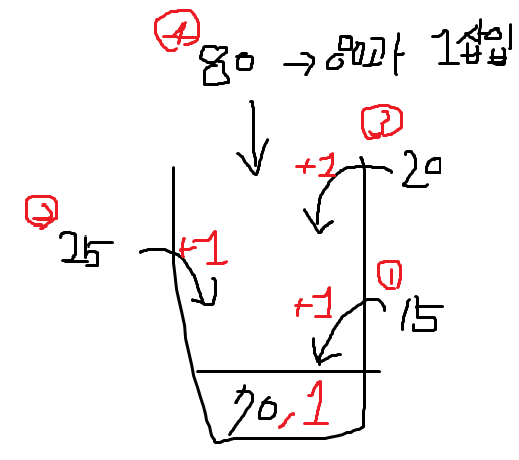
해당 코드의 로직을 그림으로 표현함.

70, 1삽입 -> 15는 70보다 작으므로 70,2 -> 25는 70보다 작으므로 70,3 -> 20은 70보다 작으므로 70, 4 -> 80은 70보다 크므로 80,1삽입
마지막에 [[70, 4], [80, 1]]에서 1번 인덱스만 리스트로 모아 출력

이게 바로 진정한 스택 아닐까...?