https://school.programmers.co.kr/learn/courses/30/lessons/42839?language=python3
문제 설명
한자리 숫자가 적힌 종이 조각이 흩어져있습니다. 흩어진 종이 조각을 붙여 소수를 몇 개 만들 수 있는지 알아내려 합니다.
각 종이 조각에 적힌 숫자가 적힌 문자열 numbers가 주어졌을 때, 종이 조각으로 만들 수 있는 소수가 몇 개인지 return 하도록 solution 함수를 완성해주세요.
제한사항
- numbers는 길이 1 이상 7 이하인 문자열입니다.
- numbers는 0~9까지 숫자만으로 이루어져 있습니다.
- "013"은 0, 1, 3 숫자가 적힌 종이 조각이 흩어져있다는 의미입니다.
입출력 예
| numbers | return |
|---|---|
| "17" | 3 |
| "011" | 2 |
입출력 예 설명
예제 #1
[1, 7]으로는 소수 [7, 17, 71]를 만들 수 있습니다.
예제 #2
[0, 1, 1]으로는 소수 [11, 101]를 만들 수 있습니다.
11과 011은 같은 숫자로 취급합니다.
시도
1
from itertools import permutations as per
def solution(numbers):
# numbers의 숫자로 이루어지는 모둔 순열
ans = list(per(numbers))
# 단일 숫자
for n in numbers:
ans.append(n)
# 조합된 숫자 합쳐서 숫자 만들기
nums = []
for ns in ans:
s = ""
for n in ns:
s += n
nums.append(int(s))
nums = set(nums) #중복제거
res = 0
# 소수 판별
for n in nums:
if n == 1 or n == 0 : continue
if isPrime(n):
res += 1
return res
def isPrime(a):
for i in range(2,a):
if(a%i==0):
return False
return True결과
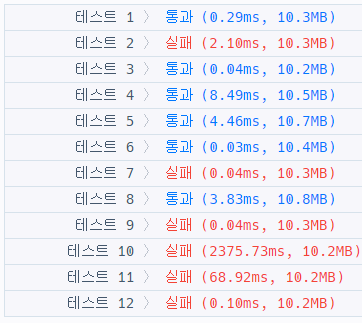
실행시간이 너무 김
순열을 구하는 데다가 일일이 isPrime()호출해대니 오래걸리는 것 같음
최종 풀이
-
조합된 숫자 합쳐서 숫자 만들기부분이 좀 허술한데"".join()으로 쉽게 해결 가능
join()을 오래 안써서 그런지 생각을 못했다# 조합된 숫자 합쳐서 숫자 만들기 nums = set() for n in ans: nums.add(int("".join(n))) -
소수 판별 부분에서 범위를 숫자의 제곱근까지 해야함.
만약에 숫자가20이면 제곱근은4.xxx니까2~4의 숫자로20을 나눠보면 됨 (20의 약수는1, 2, 4, 5, 20) -
"111"이 있을 때 결과는1이어야 하는데 0이 나옴
3-1. 내 알고리즘으로 조합했을 때{1, 111}만 나옴. 알고보니 permutations()만으로는 모든 개수의 순열조합을 구할 수 없음
=> 반복문 돌리면서 1개~문자열개수만큼의 순열 생성
from itertools import permutations as per
def solution(numbers):
# numbers의 숫자로 이루어지는 모둔 순열
ans = set()
for i in range(1, len(numbers)+1):
ans.add(per(numbers, i))
# print(ans)
# 조합된 숫자 합쳐서 숫자 만들기
nums = set()
for ns in ans:
for n in ns:
nums.add(int("".join(n)))
res = 0
# 소수 판별
for n in nums:
if n < 2 : continue
if isPrime(n):
res += 1
return res
def isPrime(a):
for i in range(2,int(a**0.5)+1):
if(a%i==0):
return False
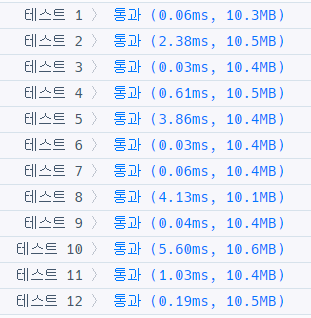
return True결과
남의 코드
from itertools import permutations
def solution(n):
a = set()
for i in range(len(n)):
a |= set(map(int, map("".join, permutations(list(n), i + 1))))
a -= set(range(0, 2))
for i in range(2, int(max(a) ** 0.5) + 1):
a -= set(range(i * 2, max(a) + 1, i))
return len(a)와 숏코딩의 천재이신듯
a |= set(map(int, map("".join, permutations(list(n), i + 1))))
순열구해서 붙어있는 숫자로 만든다음 int로 바꿔서 세트인 a에 합하기
a -= set(range(0, 2))
0, 1 차집합 (소수x)
a -= set(range(i * 2, max(a) + 1, i))
2부터 a제곱근까지의 수를 i로서 순회하면서
제일 큰 수 까지의 i의 배수들을 a에서 뺌
(에라토스테네스의 체)
이 알고리즘 짜신 분 그냥 전설인듯...
결과
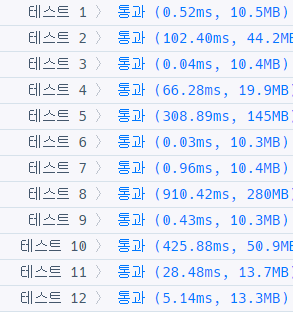
후기
완전탐색은 몇 문제를 풀어도 좀 어렵다;;;
특히나 소수가 가미된 문제라 더..
문제풀이 구조가 빨리 안 떠오른 건 아닌데 실행시간을 줄이는 방법이랑 permutations() 사용법을 제대로 몰라서 시간 많이 씀
