어떠한 기능을 구현하기 위해 다양한 코드를 작성할 수 있는 데,
이 중 기능을 가장 빠르게 실행시키고, 컴퓨터의 저장 공간을 가장 적게 사용하는 코드를 보다 좋은 코드라고 할 수 있습니다.
그런데 가장 빠른 알고리즘을 찾기 위해 코드의 실행 시간을 직접 측정해서 비교하는 것은 한계가 있습니다. 사용하는 컴퓨터의 사양, 현재 돌아가고 있는 다른 프로그램 등의 외부 환경의 영향을 받아 측정 시간이 달라질 수 있기 때문입니다.
그래서 컴퓨터 과학에서는 시간 복잡도(Time Complexity) 라는 개념을 사용합니다.
시간 복잡도
시간 복잡도란 데이터가 많아질 수록 걸리는 시간이 얼마나 급격히 증가하는지를 나타내는 개념입니다.
그래서 시간 복잡도를 비교할 때에는 데이터 증가와 걸리는 시간으로 나타낸 그래프의 경사도를 비교하게 됩니다.
| 인풋 크기 | 알고리즘A | 알고리즘B |
|---|---|---|
| 10개 | 10초 | 10초 |
| 20개 | 20초 | 40초 |
| 100개 | 100초 | 1000 초 |
| 시간복잡도 | (B보다) 크다 | (A보다) 작다 |
A가 (B보다) 더 빠른 알고리즘 / B가 A보다 더 느린 알고리즘이라고 할 수 있습니다.
점근 표기법(Big-O Notation)
어떤 알고리즘의 소요시간을 고정적인 하나의 식으로 만들어 표현하기는 어렵습니다. 컴퓨터의 성능이나 사용하는 언어 등 외부 환경에 따라 달라질 수 있기 때문입니다.
그래서 알고리즘의 속도는 걸리는 실제 시간이나 하나의 고정된 식이 아닌
완료까지 걸리는 절차의 수 로 평가되며, Big-O와 같은 표기법으로 표기합니다.
| 소요시간 | 점근 표기법(Big-O) |
|---|---|
| 20n + 40 | O(n) |
| 20n² + 8n + 157 | O(n²) |
| 5n³ + 199n² + 1 | O(n³) |
| 20lgn + 60 | O(lgn) |
Big-O(빅-오) 표기 법 외에도 Big-Ω(빅-오메가)(최선의 경우일 때)
Big-θ(빅-세타)(평균의 경우일 때)도 있지만,
해당 알고리즘이 빠른(좋은) 알고리즘인지를 확인하려면 실행 횟수가 엄청나게 많을 때를 생각해보아야 합니다. 나쁜(느린) 알고리즘이더라도 실행 횟수가 적을 때 걸리는 시간은 얼마되지 않아 사용할 때 별로 불편을 느끼지 않을테니까요.
또 최악의 경우(실행 횟수가 엄청나게 많은 경우)를 가정해야, 실행 속도가 최대 어느 정도까지 걸릴지 예측할 수 있고, 예상 시간보다 오래 걸렸을 때의 문제를 보다 빠르게 파악할 수 있을 것입니다.
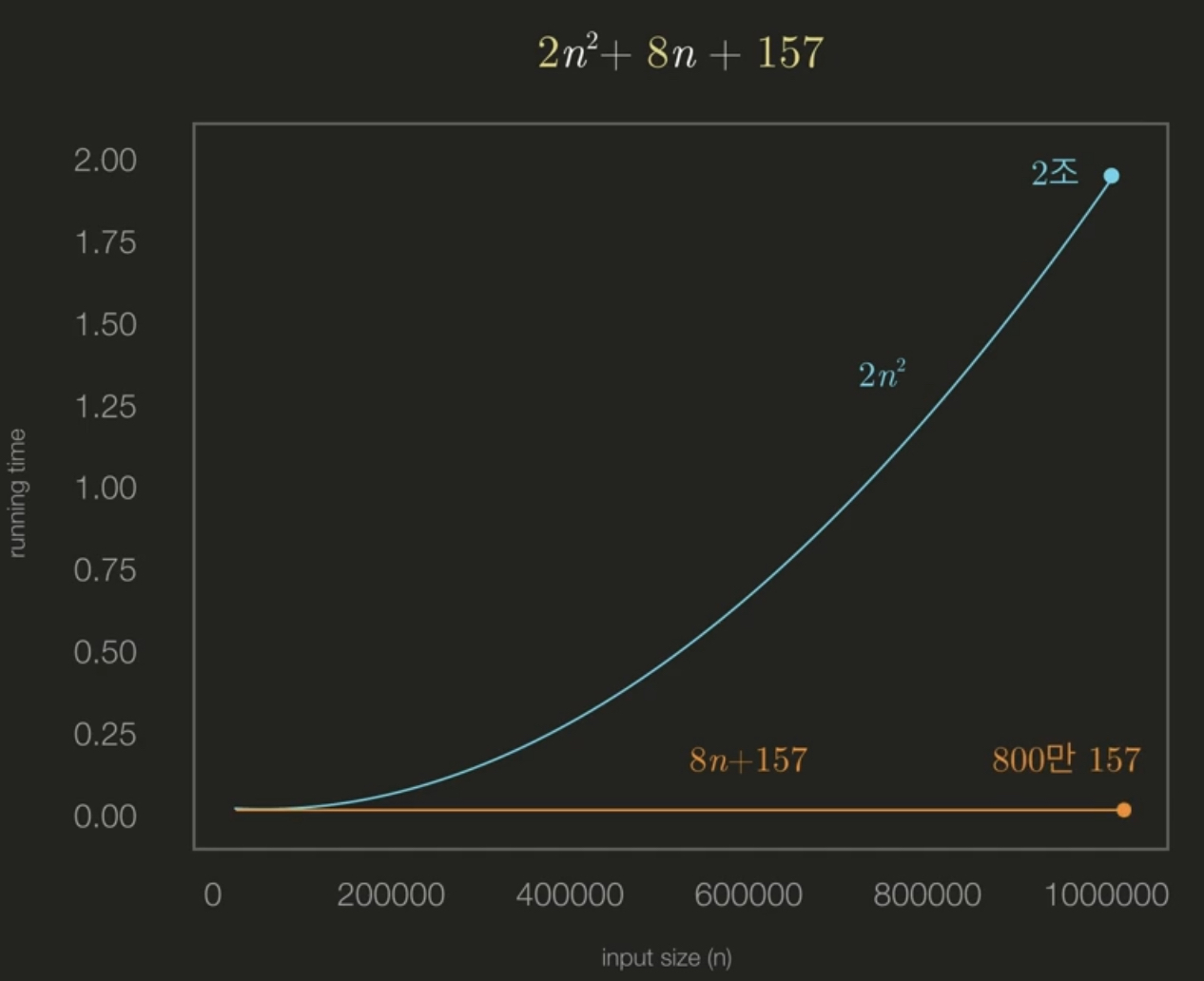
따라서 점근 표기법은 투입되는 데이터의 크기(n)가 엄청 크다고 가정하고,
결과에 유의미한 영향을 미치지 못하는 요소들은 모두 무시해버립니다.
또한 실제로 몇 초가 걸리는지는 중요하지 않고, 데이터 크기가 커짐에 따라 변화되는 성장성이 중요하므로 n 앞의 상수도 무시하게 됩니다.
점근 표기법(Big-O)의 표현들의 의미

자주 쓰이는 O(1), O(n), O(n²), O(lg n), O(nlgn) 가 있고, 그 외에도 O(n^m), O(2ⁿ), O(sqrt(n)), O(n!) 등의 표현들이 있습니다.
아래 설명의 time은 실행되는 절차의 수을 말합니다.
O(1) : 데이터의 크기에 상관없이 항상 1 time이 걸립니다.
- 상수 시간(constant time)이 걸리는 경우는 모두 O(1)으로 표기합니다.
- 시간 복잡도의 개념인 '얼마나 급격히 증가'가 중요하기 때문입니다.
let numbers = [1, 2, 3, 4, 5];
function print(){
console.log(numbers);
}
// 시간복잡도가 O(1) 입니다.
print(); // [ 1, 2, 3, 4, 5 ]O(n) : 데이터의 크기와 비례해서 소요되는 time이 증가합니다.
- 주로 반복문이 있고, 반복되는 횟수가 인풋의 크기와 비례할 때 O(n)의 시간복잡도를 가집니다.
let numbers = [1, 2, 3, 4, 5];
function print() {
for (num of numbers) {
console.log(num);
}
}
// 시간복잡도가 O(n) 입니다.
print(); // 1 2 3 4 5
// 1/2번 반복해도 시간 복잡도는 O(n) 입니다. O(1/2n)아님 주의
function print2(ary) {
for (i = 0; i < parseInt((ary.length)/2); i++) {
console.log(ary[i]);
}
}
print2(numbers); // 1 2O(n²) : 데이터의 크기가 증가할 수록 소요되는 time이 제곱해서 증가합니다.
- 주로 반복문이 중첩되어 있는 경우 O(n²) 시간 복잡도를 가집니다.
- 비슷한 원리로 반복문이 세 번 중첩되면 O(n³)이 됩니다.
let numbers = [[1, 2], [3, 4], [5, 6]];
function print(){
for(ary of numbers){
for(num of ary){
console.log(num);
}
}
}
// 시간복잡도가 O(n²) 입니다.
print(); // 1 2 3 4 5 6 O(lg n) : 데이터가 2배로 증가해도 소요 시간은 1 time만 증가합니다.
- log₂n을 lg n으로 생략해서 표현할 수 있습니다.
- 이진 탐색 알고리즘의 시간 복잡도를 표현할 수 있습니다.
- 단 이진 탐색 알고리즘은 정렬되지 않은 배열에서는 사용할 수 없습니다.
// 반복문을 돌게 할 지 평가하는 변수 i가 절반씩 줄어듦
function divisionTwo(num) {
let i = num;
while (i > 0) {
console.log(i);
i = parseInt(i / 2);
}
}
// 시간복잡도가 O(lg n) 입니다.
divisionTwo(10); // 10 5 2 1// 반복문의 변수 i 가 2배씩 증가
let numbers = [1, 2, 3, 4, 5];
function f(n) {
for (let i = 0; i < n.length; i = i * 2) {
console.log(n[i]);
if (i === 0) i++;
}
}
//시간복잡도가 O(lg n) 입니다.
f(numbers); // 1, 3, 5 O(nlgn) : O(n)과 O(lg n)이 중첩되었을 때
let numbers = [[1, 2], [3, 4], [5, 6]];
function print(ary) {
for (let i = 0; i < ary.length; i++) {
for (let j = 0; j < ary[i].length; j *= 2) {
console.log(ary[i][j]);
if (j === 0) j++;
}
}
}
print(numbers); // 1 3 5